Skip to main content
SpringerLink
Log in

Machine Learning Neural-Network Predictions for Grain-Boundary Strain Accumulation in a Polycrystalline Metal

  • Research paper
  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

Background

Microstructural features such as grain boundaries play a significant role in the macroscopic plastic response of polycrystalline metals. However, a quantitative link between plastic strain accumulation at grain boundaries and material response in plasticity dominated phenomena is still lacking.

Objective

Here we seek to develop predictive relations between a material’s granular microstructure and the accumulation of plastic strains at the microstructural level during plastic deformation.

Methods

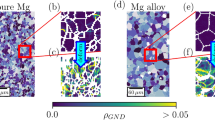
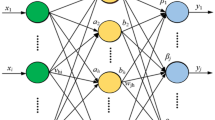
A single-input neural network approach was applied to predict the residual plastic strain fields at regions surrounding grain boundaries of an austenitic stainless steel. The neural network was trained on data obtained by applying a very-high resolution digital image correlation (DIC) experimental technique that allows the measurement of grain-scale strains aligned to the underlying microstructure obtained from electron backscatter diffraction (EBSD) scans.

Results

The neural-network-predicted and the DIC-measured strain fields showed good correlation for most of the tested cases. Best individual agreement was found when each microstructure was used to predict fields in its own case. However, best overall average predictions were seen when multiple samples were used for the network training.

Conclusions

The results showed that the local geometrical angle between a grain boundary and the loading axes is in many cases a good predictor for the accumulation of strains at the given boundary. The expected limitations of this single parameter approach (grain boundary angle alone cannot be a good predictor for varying strains along a straight grain boundary, for example) were seen as the reason for the situations where predictions were not as good.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Eshelby J, Frank F, Nabarro F (1951) The equilibrium of linear arrays of dislocations. Philos Mag 42:351–364

    Article  MathSciNet  Google Scholar 

  2. Petch NJ (1953) The cleavage strength of polycrystals. J Iron Steel Inst 174:25–28

    Google Scholar 

  3. Hall E (1951) The deformation and aging of mild steel:III. Discussion of results. Proc Phys Soc Lond 38(10):747–753

    Article  Google Scholar 

  4. Sutton AP, Balluffi RW (2006) Interfaces in crystalline materials. Oxford University Press, Oxford

    Google Scholar 

  5. Lee TC, Robertson IM, Birnbaum H (1989) Prediction of slip transfer mechanisms across grain boundaries. Scr Metall 23(5):799

    Article  Google Scholar 

  6. Jin ZH, Gumbsch P (2008) Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater 56(5):1126

    Article  Google Scholar 

  7. Abuzaid W, Sangid M, Carroll J, Sehitoglu H (2012) Slip transfer and plastic strain accumulation across grain boundaries in Hastelloy X. J Mech Phys Solids 60(6):1201–1220

    Article  Google Scholar 

  8. Abuzaid W, Sehitoglu H, Lambros J (2013) Plastic strain localization and fatigue micro-crack formation in Hastelloy X. Mater Sci Eng A 561:507–519

    Article  Google Scholar 

  9. Figueroa J, Laird C (1983) Crack initiation mechanisms in copper polycrystals cycled under constant strain amplitudes and in step tests. Mater Sci Eng 60(1):45–58

    Article  Google Scholar 

  10. Chan K (2010) Roles of microstructure in fatigue crack initiation. Int J Fatigue 32(9):1428–1447

    Article  Google Scholar 

  11. Carroll J, Abuzaid W, Lambros J, Sehitoglu H (2013) On the interactions between strain accumulation, microstructure, and fatigue crack behavior. Int J Fract 180:223–241

    Article  Google Scholar 

  12. Littlewood P, Wilkinson A (2014) Local deformation patterns in Ti-6Al-4V under tensile, fatigue and dwell fatigue loading. Int J Fatigue 43:111–119

    Article  Google Scholar 

  13. Gurney K (1997) An introduction to neural networks. UCL Press, London

    Book  Google Scholar 

  14. McCulloch W, Pitts W (1943) A logical calculus of the ideas immanent in nervous activity. Math Biophysics 7:115–133

    Article  MathSciNet  Google Scholar 

  15. Sourmail T, Bhadeshia H, MacKay D (2002) Neural network model of creep strength of austenitic stainless steels. Mater Sci Technol 18:655–663

    Article  Google Scholar 

  16. Lee D, Hong S, Cho S, Joo W (2005) A study on fatigue damage modeling using neural networks. J Mech Sci Technol 19(7):1393–1404

    Article  Google Scholar 

  17. Kang J, Choi B, Lee H, Kim J, Kim K (2006) Neural network application in fatigue damage analysis under multiaxial random loadings. Int J Fatigue 28(2):132–140

    Article  Google Scholar 

  18. Pujol J, Pinto J (2011) A neural network approach to fatigue life prediction. Int J Fatigue 33(3):313–322

    Article  Google Scholar 

  19. Martinez M, Ponce M (2019) Fatigue damage effect approach by artificial neural network. Int J Fatigue 124:42–47

    Article  Google Scholar 

  20. Mozaffar M, Bostanabad R, Chen W, Ehman K, Cao J, Bessa MA (2019) Deep learning predicts path-dependent plasticity. Proc Natl Acad Sci USA 116(52):26414–26420. https://doi.org/10.1073/pnas.1911815116

    Article  Google Scholar 

  21. Lin Y, Zhang J, Zhong J (2008) Application of neural networks to predict the elevated temperature. Comput Mater Sci 43(4):752–758

    Article  Google Scholar 

  22. Li H-Y, Wang X-F, Wei D-D, Hu J-D, Li Y-H (2012) A comparative study on modified zerilli–Armstrong, arrhenius-type and artificial neural network models to predict high-temperature deformation behavior in t24 steel. Mater Sci Eng 536:216–222

    Article  Google Scholar 

  23. Jones R, Templeton J, Sanders C, Ostien J (2018) Machine learning models of plastic flow based on representation theory. Comput Model Eng Sci 117:309–342

    Google Scholar 

  24. Carroll J, Abuzaid W, Lambros J, Sehitoglu H (2010) An experimental methodology to relate local strain to microstructural texture. Rev Sci Instrum 81(8):083703

    Article  Google Scholar 

  25. Swati U, Li H, Bowen P, Rabiei A (2018) A study on tensile properties of alloy 709 at various temperatures. Mater Sci Eng A 733:338–349

    Article  Google Scholar 

  26. Naoi H, Mimura H, Ohgami M, Sakakibara M, Araki S, Sogoh Y, Ogawa T, Sakurai H, Fujita T (1993) Development of tubes and pipes for ultra-supercritical thermal power plant boilers. Nippon Steel Tech Rep 57:22–27

    Google Scholar 

  27. Ding R, Yan J, Li H, Yu S, Rabiei A, Bowen P (2019) Deformation microstructure and tensile properties of alloy 709 at different temperatures. Mater Des 176

  28. Sourmail T, Bhadeshia H (2005) Microstructural evolution in two variants of NF709 at 1023 and 1073 K. Metall Mater Trans A 36(1):23–34

    Article  Google Scholar 

  29. Lall A, Sarkar S, Ding R, Bowen P, Rabiei A (2019) Performance of alloy 709 under creep-fatigue at various dwell times. Mater Sci Eng A 761:138028

    Article  Google Scholar 

  30. Shaber N, Stephens R, Ramirez J, Potirniche G, Taylor M, Charit I, Pugesek H (2019) Fatigue and creep-fatigue crack growth in alloy 709 at elevated temperatures. Mater High Temp 36(6):562–574

    Article  Google Scholar 

  31. Sutton M, Wolters W, Peters W, Ranson W, McNeill S (1983) Determination of displacements using an improved digital correlation method. Image Vis Comput 1(3):133–139

    Article  Google Scholar 

  32. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, Tinevez J, White DJ, Hartenstein V, Eliceiri K, Tomancak P, Cardona A (2012) Fiji: an open-source platform for biological-image analysis. Nat Methods 9(7):676–682

    Article  Google Scholar 

  33. Wilkinson A, Britton T (2012) Strains, planes, and EBSD in materials science. Mater Today 15(9):366–376

    Article  Google Scholar 

  34. Meyers MAE (1982) Model for the effect of grain size on the yield stress of metals. Philos Mag A 46(5):737–759

    Article  Google Scholar 

  35. Marquardt D (1963) An algorithm for least-squares estimation of nonlinear parameters. SIAM J Appl Math 11(2):431–441

    Article  MathSciNet  Google Scholar 

  36. MathWorks, (2020). Deep Learning Toolbox: User’s Guide (R2020b). Retrieved October 22, 2020 from https://www.mathworks.com/help/pdf_doc/deeplearning/nnet_ug.pdf

Download references

Acknowledgements

This research was performed in part using funding received from the Department of Energy Office of Nuclear Energy’s Nuclear Energy University Program under grant number DE-NE0008436 (Project number 15-8432). The work was carried out in part in the Materials Research Laboratory Central Research Facilities University of Illinois (EBSD measurements), and the Advanced Materials Testing and Evaluation Laboratory University of Illinois (mechanical testing).

Author information

Authors and Affiliations

  1. Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, 61801, USA

    R. B. Vieira & J. Lambros

Authors
  1. R. B. Vieira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Lambros
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. Lambros.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vieira, R.B., Lambros, J. Machine Learning Neural-Network Predictions for Grain-Boundary Strain Accumulation in a Polycrystalline Metal. Exp Mech 61, 627–639 (2021). https://doi.org/10.1007/s11340-020-00687-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-020-00687-1

Keywords

Search

Navigation