Skip to main content
SpringerLink
Log in

On Evaluation of Stress Intensity Factor from In-Plane and Transverse Surface Displacements

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

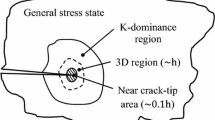
Abstract

Experimental approaches to the evaluation of stress intensity factor (SIF) of through-cracked plate components are currently based on the classical plane stress (2D) asymptotic power series expansion of strains or displacements near the crack tip (Williams’ solution). Besides the plasticity effects, the quantitative evaluation of SIF has to take into account a finite domain of convergence of the series expansion as well as three-dimensional (3D) effects, which prevail in the close vicinity of the crack tip. In this paper we demonstrate and confirm that attempts to fit Williams’ solution to experimental data in the near crack tip region can provide misleading results. In addition, it is verified that the SIF can be linked to the transverse displacements in the region controlled by 3D effects, and in particular, by 3D corner singularity. Under mode I loading, the transverse displacement field in this region is uniform, and largely unaffected by the higher order terms of the asymptotic power series expansion, which make this way of the evaluation of SIF particularly attractive for experimental measurements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Rooke DP, Cartwright DJ (1976) Compendium of stress intensity factors. Her Majesty’s Stationery Office, London

  2. Tada H, Paris PC, Irwin GR (1985) The stress analysis of cracks handbook. Paris Productions, St. Louis, Mo

    Google Scholar 

  3. Murakami Y (1987) Stress intensity factors handbook. Pergamon Press, New York

    Google Scholar 

  4. Lim I, Johnston IW, Choi SK (1992) On stress intensity factor computation from the quarter-point element displacements. Commun Appl Numer Methods 8:291–300

    Article  MATH  Google Scholar 

  5. Courtin S, Gardin C, Bezine G, Hamouda HBH (2005) Advantages of the J-integral approach for calculating stress intensity factors when using the commercial finite element software ABAQUS. Eng Fract Mech 72:2174–2185

    Article  Google Scholar 

  6. Pak YE, Kim S (2010) On the use of path-independent integrals in calculating mixed-mode stress intensity factors for elastic and thermoelastic cases. J Therm Stresses 33:661–673

    Article  Google Scholar 

  7. Theocaris PS (1984) Experimental methods for determining stress intensity factors. Int J Fract Mech 1:707–728

    Google Scholar 

  8. Wei J, Zhao JH (1997) A two-strain-gage technique for determining mode I stress-intensity factor. Theor Appl Fract Mech 28:135–140

    Article  Google Scholar 

  9. Dorogoy A, Rittel D (2008) Optimum location of a three strain gauge rosette for measuring mixed mode stress intensity factors. Eng Fract Mech 75:4127–4139

    Article  Google Scholar 

  10. Humbert L, Valle V, Cottron M (2000) Experimental determination and empirical representation of out-of-plane displacements in a cracked elastic plate loaded in mode I. Int J Solids Struct 37:5493–5504

    Article  MATH  Google Scholar 

  11. Ravi-Chandar K (2008) Fracture mechanics. In: Sharpe WN (ed) Springer handbook of experimental solid mechanics. Springer Science + Business Media, New York, pp 125–158

    Chapter  Google Scholar 

  12. Baik MC, Choi SH, Hawong JS, Kwon JD (1995) Determination of stress-intensity factors by the method of caustics in anisotropic materials. Exp Mech 35:137–143

    Article  Google Scholar 

  13. Yazdanmehr A, Soltani N (2014) Evaluation of stress intensity factors of rounded V and U notches under mixed mode loading, using the experimental method of caustics. Theor Appl Fract Mech 74:79–85

    Article  Google Scholar 

  14. Ayatollahi MR, Nejati M (2011) Experimental evaluation of stress field around the sharp notches using photoelasticity. Mater Des 32:561–569

    Article  Google Scholar 

  15. Sutton MA, Yan JH, Tiwari V, Schreier HW, Orteu JJ (2008) The effect of out-of-plane motion on 2D and 3D digital image correlation measurements. Opt Lasers Eng 46:746–757

    Article  Google Scholar 

  16. Sutton MA, Orteu JJ, Schreier HW (2009) Image correlation for shape, motion and deformation measurements. Springer, New York

    Google Scholar 

  17. McCormick N, Lord J (2010) Digital image correlation. Mater Today 13:52–54

    Article  Google Scholar 

  18. Brynk T, Laptiev A, Tolochyn O, Pakiela Z (2012) The method of fracture toughness measurements of high speed camera and DIC. Comput Mater Sci 64:221–224

    Article  Google Scholar 

  19. McNeill SR, Peters WH, Sutton MA (1987) Estimation of stress intensity factor by digital image correlation. Eng Fract Mech 28:101–112

    Article  Google Scholar 

  20. Roux S, Hild F (2006) Stress intensity factor measurements from digital image correlation: post-processing and integrated approaches. Int J Fract 140:141–157

    Article  MATH  Google Scholar 

  21. Réthoré J, Gravouil A, Morestin F, Combescure A (2005) Estimation of mixed-mode stress intensity factors using digital image correlation and an interaction integral. Int J Fract 132:65–79

    Article  Google Scholar 

  22. Pataky GJ, Sangid MD, Sehitoglu H, Hamilton RF, Maier HJ, Sofronis P (2012) Full field measurements of anisotropic stress intensity factor ranges in fatigue. Eng Fract Mech 94:13–18

    Article  Google Scholar 

  23. He Z, Kotousov A, Fanciulli A, Berto F, Nguyen G (2015) On the evaluation of stress intensity factor from displacement field affected by 3D corner singularity. Int J Solids Struct 78–79:131–137

    Google Scholar 

  24. Rosakis AJ, Ravi-Chandar K (1983) On crack-tip stress state: an experimental evaluation of three-dimensional effects. Int J Solids Struct 22:121–134

    Article  Google Scholar 

  25. Kotousov A (2010) Effect of plate thickness on stress state at sharp notches and the strength paradox of thick plates. Int J Solids Struct 47:1916–1923

    Article  MATH  Google Scholar 

  26. Berto F, Lazzarin P, Kotousov A (2011) On the presence of the out-of-plane singular mode induced by plane loading with KII = KI = 0. Int J Fract 167:119–126

    Article  MATH  Google Scholar 

  27. He Z, Kotousov A, Berto F (2015) Effect of vertex singularities on stress intensities near plate free surfaces. Fatigue Fract Eng Mater Struct 38:860–869

    Article  Google Scholar 

  28. She C, Guo W (2007) The out-of-plane constraint of mixed-mode cracks in thin elastic plates. Int J Solids Struct 44:3021–3034

    Article  MATH  Google Scholar 

  29. Berto F, Lazzarin P, Kotousov A (2011) On higher order terms and out of plane singular mode. Mech Mater 43:332–341

    Article  MATH  Google Scholar 

  30. Kotousov A, Lazzarin P, Berto F, Pook LP (2013) Three-dimensional stress states at crack tip induced by shear and anti-plane loading. Eng Fract Mech 108:65–74

    Article  Google Scholar 

  31. Pook LP (2013) A 50-years retrospective review of three-dimensional effects at cracks and sharp notches. Fatigue Fract Eng Mater Struct 36:699–723

    Article  Google Scholar 

  32. Hello G, Tahar MB, Roelandt J-M (2012) Analytical determination of coefficients in crack-tip stress expansions for a finite crack in an infinite plane medium. Int J Solids Struct 49:556–566

    Article  Google Scholar 

  33. Kotousov A, Berto F, Lazzarin P, Pegorin F (2012) Three dimensional finite element mixed fracture mode under anti-plane loading of a crack. Theor Appl Fract Mech 62:26–33

    Article  Google Scholar 

  34. Liao M, Tang A, Hu Y, Guo Z (2015) Computation of coefficients of crack-tip asymptotic fields using the weak form quadrature element method. J Eng Mech 141

  35. Ayatollahi MR, Aliha MRM, Saghafi H (2011) An improved semi-circular bend specimen for investigating mixed mode brittle fracture. Eng Fract Mech 78:110–123

    Article  Google Scholar 

  36. Gómez FJ, Elices M (2003) A fracture criterion for sharp V-notched samples. Int J Fract 123:163–175

    Article  MATH  Google Scholar 

  37. Berto F, Lazzarin P, Kotousov A, Pook LP (2012) Induced out-of-plane mode at the tip of blunt lateral notches and holes under in-plane shear loading. Fatigue Fract Eng Mater Struct 35:538–555

    Article  Google Scholar 

  38. Williams ML (1957) On the stress distribution at the base of a stationary crack. J Appl Mech 24:109–114

    MathSciNet  MATH  Google Scholar 

  39. Yang W, Freund LB (1984) Transverse shear effects for through-cracks in an elastic plate. Int J Solids Struct 21:977–994

    Article  MathSciNet  MATH  Google Scholar 

  40. He Z, Kotousov A, Berto F, Branco R (2016) A brief review of recent three-dimensional studies of brittle fracture. Phys Mesomech 19:6–20

    Article  Google Scholar 

Download references

Acknowledgments

Financial support for the purchase of the DIC equipment from the Faculty of Engineering, Computer and Mathematical Sciences, University of Adelaide, is gratefully acknowledged.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, The University of Adelaide, Adelaide, SA, 5005, Australia

    Z. He & A. Kotousov

Authors
  1. Z. He
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Kotousov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Kotousov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, Z., Kotousov, A. On Evaluation of Stress Intensity Factor from In-Plane and Transverse Surface Displacements. Exp Mech 56, 1385–1393 (2016). https://doi.org/10.1007/s11340-016-0176-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11340-016-0176-8

Keywords

Search

Navigation