Abstract
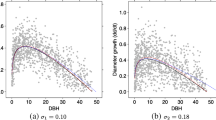
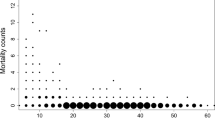
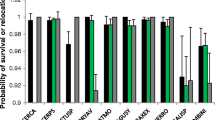
When we calculate mortality along a gradient such as size, dividing into size classes and calculating rates for every class often involves a trade-off: fine class intervals produce fluctuating rates along the gradient, whereas broad ones may miss some trends within an interval. The same trade-off occurs when we want to illustrate size distribution by a histogram. This paper introduces nonparametric methods, published in a statistical journal, into forest ecology, in which the fine-class strategy is used in an extreme way: (1) a smoothly changing pattern is approximated by a fine step function, (2) the goodness-of-fit to the data and the smoothness along the gradient are formulated as a weighting sum within a Bayesian framework, (3) the Akaike Bayesian Information Criterion (ABIC) selects the weighting system that most appropriately balances the two demands, and (4) the values of the step function are optimized by the maximum likelihood method. The nonparametric estimates enable us to represent various patterns visually and, unlike parametric modeling, calculations do not demand the determination of a functional form. Mortality and size distribution analyses were conducted on 12-year forest tree monitoring data from a 4 ha permanent plot in an old-growth warm–temperate evergreen broad-leaved forest in Japan. From trees of 11 evergreen species with a diameter at breast height (DBH) greater than 5 cm, we found three types of trend with increasing DBH: decreasing, ladle-shaped and constant mortality. These patterns reflect variations in life history particular to each species.

Similar content being viewed by others
References
Akaike H (1980a) On the use of predictive likelihood of a Gaussian model. Ann Inst Stat Math 32:311–324
Akaike H (1980b) Likelihood and the Bayes procedure. In: Bernardo NJ, DeGroot MH, Lindley DV, Smith AFM (eds) Bayesian statistics. University Press, Valencia pp 141–166
Ayer M, Brunk HD, Ewing GM, Reid WT, Silverman E (1995) An empirical distribution function for sampling with incomplete information. Ann Math Stat 26:641–617
Barndorff-Nielsen OE, Cox DR (1989) Asymptotic techniques for use in statistics. Chapman and Hall, London
Beckage B, Clark JS (2003) Seedling survival and growth of three forest tree species: the role of spatial heterogeneity. Ecology 84:1849–1861
Bigler C, Bugmann H (2003) Growth-dependent tree mortality models based on tree rings. Can J For Res 33:210–221
Carey EV, Brown S, Gillespie AJR, Lugo AE (1994) Tree mortality in mature lowland tropical moist and tropical lower montane moist forests of Venezuela. Biotropica 26:255–265
Caspersen JP, Kobe RK (2001) Interspecific variation in sapling mortality in relation to growth and soil moisture. Oikos 92:160–168
Condit R, Hubbell SP, Foster RB (1995) Mortality rates of 205 neotropical tree and shrub species and the impact of a severe drought. Ecol Monogr 65:419–439
Davies SJ (2001) Tree mortality and growth in 11 sympatric Macaranga species in Borneo. Ecology 82:920–932
Duchesne L, Ouimet R, Moore J-D, Paquin R (2005) Changes in structure and composition of maple-beech stands following sugar maple decline in Québec, Canada. For Ecol Manage 208:223–236
Eggermont PPB, LaRiccia VN (2001) Maximum penalized likelihood estimation, vol I. Density estimation. Springer, Heidelberg
Franklin JF, Shugart HH, Harmon ME (1987) Tree death as an ecological process. Bioscience 37:550–556
Fujita T, Itaya A, Miura M, Manabe T, Yamamoto S (2003) Long-term canopy dynamics analyzed by aerial photographs in a temperate old-growth evergreen broad-leaved forest. J Ecol 91:686–693
Gratzer G, Canham C, Dieckmann U, Fischer A, Iwasa Y, Law R, Lexer MJ, Sandmann H, Spies TA, Splechtna BE, Szwagrzyk J (2004) Spatio-temporal development of forests—current trends in field methods and models. Oikos 107:3–15
Harcombe PA (1987) Tree life tables. BioScience 37:557–568
Hély C, Flannigan M, Bergeron Y (2003) Modeling tree mortality following wildfire in the southeastern Canadian mixed-wood boreal forest. For Sci 49:566–575
Ishiguro M, Sakamoto Y (1983) A Bayesian approach to binary response curve estimation. Ann Inst Stat Math B 35:115–137
Ishiguro M, Sakamoto Y (1984) A Bayesian approach to the probability density estimation. Ann Inst Stat Math B 36:523–538
Ishiguro M, Sakamoto Y, Kitagawa G (1997) Bootstrapping log likelihood and EIC, an extension of AIC. Ann Inst Stat Math 49:411–434
Kohyama T (1993) Size-structured tree population in gap-dynamic forest—the forest architecture hypothesis for the stable coexistence of species. J Ecol 81:131–143
Kubota Y, Hara T (1995) Tree competition and species coexistence in a sub-boreal forest, northern Japan. Ann Bot 76:503–512
Lorimer CG, Dahir SE, Nordheim EV (2001) Tree mortality rates and longevity in mature and old-growth hemlock-hardwood forests. J Ecol 89:960–971
Manabe T, Nishimura N, Miura M, Yamamoto S (2000) Population structure and spatial patterns for trees in a temperate old-growth evergreen broad-leaved forest in Japan. Plant Ecol 151:181–197
Miura M, Manabe T, Nishimura N, Yamamoto S (2001) Forest canopy and community dynamics in a temperate old-growth evergreen broad-leaved forest, south-western Japan: a 7-year study of a 4-ha plot. J Ecol 89:841–849
Moloney KA (1986) A generalized algorithm for determining category size. Oecologia 69:176–180
Monserud RA (1976) Simulation of forest tree mortality. For Sci 22:438–444
Monserud RA, Sterba H (1999) Modeling individual tree mortality for Austrian forest species. For Ecol Manage 113:109–123
Nishimura N, Hara T, Miura M, Manabe T, Yamamoto S (2002) Tree competition and species coexistence in a warm-temperate old-growth evergreen broad-leaved forest in Japan. Plant Ecol 164:235–248
Parker GR, Jeopold DJ, Eichenberger JK (1985) Tree dynamics in an old-growth, deciduous forest. For Ecol Manage 11:31–57
Picard N, Bar-Hen A, Guédon Y (2003) Modelling diameter class distribution with a second-order matrix model. For Ecol Manage 180:389–400
Platt WJ, Evans GW, Rathbun SL (1988) The population dynamics of a long-lived conifer (Pinus palustris). Am Nat 131:491–525
Sakamoto Y (1991) Categorical data analysis by AIC. Kluwer, Dordrecht
Sheil D, May RM (1996) Mortality and recruitment rate evaluations in heterogeneous tropical forests. J Ecol 84:91–100
Ueno S, Tomaru N, Yoshimaru H, Manabe T, Yamamoto S (2002) Size-class differences in genetic structure and individual distribution of Camellia japonica L. in a Japanese old-growth evergreen forest. Heredity 89:120–126
Vandermeer J (1978) Choosing category size in a stage projection matrix. Oecologia 32:79–84
Woodall CW, Grambsch PL, Thomas W, Moser WK (2005) Survival analysis for a large-scale forest health issue: Missouri oak decline. Environ Monit Assess 108:295–307
Woods KD (2000) Dynamics in late-successional hemlock-hardwood forests over three decades. Ecology 81:110–126
Woods KD (2004) Intermediate disturbance in a late-successional hemlock-northern Hardwood forest. J Ecol 92:464–476
Wyckoff PH, Clark JS (2000) Predicting tree mortality from diameter growth: a comparison of maximum likelihood and Bayesian approaches. Can J For Res 30:156–167
Yang Y, Stephen JT, Huang S (2003) Modeling individual tree mortality for white spruce in Alberta. Ecol Model 163:209–222
Zhao D, Borders B, Wilson M (2004) Individual-tree diameter growth and mortality models for bottomland mixed-species hardwood stands in the lower Mississippi alluvial valley. For Ecol Manage 199:307–322
Acknowledgments
We wish to thank to Dr. Yamamoto, Dr. Aikawa, Dr. Charles Rose, Dr. Barry W. Brook and an anonymous referee for their useful comments and suggestions. This study was supported by a Grant-in-Aid for Science Research (No. 14206017 and 16380111) from the Ministry of Education, Science, Sports and Culture, and by the ISM Cooperative Research program (2004, ISM-CRP-2048, 2005, ISM-CRP-2041) and ISM Project Research 2004.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Shimatani, K., Kawarasaki, S. & Manabe, T. Describing size-related mortality and size distribution by nonparametric estimation and model selection using the Akaike Bayesian Information Criterion. Ecol Res 23, 289–297 (2008). https://doi.org/10.1007/s11284-007-0375-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11284-007-0375-y