Skip to main content
SpringerLink
Log in

Low-Computation GNSS Acquisition Method for Sparse Doppler Frequency Hypotheses in High-Dynamic Environment

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

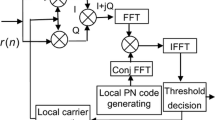
Abstract

To acquire Global Navigation Satellite System (GNSS) signal in high-dynamic and long integration applications, the high dimensional search of this detection needs a high computational cost. To reduce the computations of parameters estimation, this paper proposes a low-computation GNSS acquisition method (LGAM) in the high-dynamic environment. Firstly, sparse Doppler frequency (SDF) process is performed for SDF hypotheses, and post-correlation signal model is derived based on SDF structure. Then, double-FFT based detection is proposed based on the post-correlation signal model for parameters estimation. The results demonstrate that due to the reduction of complex multiplications, the computational cost of LGAM is lower than that of the FFT based methods under the moderate signal to noise ratio.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Availability of Data and Materials

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study. Consent for publication The manuscript does not contain any individual person’s data in any form (including individual details, images, or videos) and therefore the consent to publish is not applicable to this article.

Abbreviations

BPSK:

Binary phase shift keying

FAP:

False alarm probability

GNSS:

Global Navigation Satellite System

IT:

Integration times

LGAM:

Low-computation GNSS acquisition method

SDF:

Sparse Doppler frequency

SNR:

Signal to noise ratio

SDHT:

Synthesized Doppler frequency hypothesis testing

MAC:

Mean acquisition computation

DCFT:

Discrete chirp-Fourier transform

FFT:

Fast Fourier transform

References

  1. Kong, S. H. (2017). High Sensitivity and Fast Acquisition Signal Processing Techniques for GNSS Receivers: From fundamentals to state-of-the-art GNSS acquisition technologies. IEEE Signal Processing Magazine, 34(5), 59–71.

    Article  Google Scholar 

  2. Cismaru, A., Spens, N., & Akos, D. M. (2023). Future GNSS acquisition strategies and algorithms. In Proceedings of the 36th international technical meeting of the satellite division of the institute of navigation (ION GNSS+ 2023) (pp. 3343–3352).

  3. Xie, F., Sun, R., Kang, G., et al. (2017). A jamming tolerant BeiDou combined B1/B2 vector tracking algorithm for ultra-tightly coupled GNSS/INS systems. Aerospace Science and Technology, 70, 265–276.

    Article  Google Scholar 

  4. Guo, W., Niu, X., Guo, C., et al. (2016). A new FFT acquisition scheme based on partial matched filter in GNSS receivers for harsh environments. Aerospace Science and Technology, 61, 66–72.

    Article  Google Scholar 

  5. Qing, X. Z., Chang, G., Wen, Q. Q., et al. (2020). Parallel Frequency Acquisition Algorithm for BeiDou Software Receiver Based on Coherent Downsampling. Journal of Navigation, 73(2), 433–454.

    Article  Google Scholar 

  6. Zhang, H., Xu, Y., Luo, R., et al. (2023). Fast GNSS acquisition algorithm based on SFFT with high noise immunity. China Communications.

  7. Wu, C., & Gao, Y. (2020). Low-computation GNSS signal acquisition method based on a complex signal phase in the presence of sign transitions. IEEE Transactions on Aerospace and Electronic Systems, 56(6), 4177–4191.

    Article  Google Scholar 

  8. Kong, S. H., & Kim, B. (2013). Two-dimensional compressed correlator for fast PN code acquisition. IEEE Transactions on Wireless Communications, 12(11), 5859–5867.

    Article  Google Scholar 

  9. Ju, Z., Chen, L., & Yan, J. (2023). Acquisition of weak BDS signal in the lunar environment. Remote Sensing, 15(9), 2445.

    Article  Google Scholar 

  10. Kong, S. H. (2015). SDHT for fast detection of weak GNSS signals. IEEE Journal on Selected Areas in Communications, 33(11), 2366–2378.

    Article  Google Scholar 

  11. Yang, C., Nguyen, T., Blasch, E., et al. (2008). Post-correlation semi-coherent integration for high-dynamic and weak GPS signal acquisition. In Position, location & navigation symposium, IEEE/ION (pp. 1341–1349). IEEE.

  12. Yu, W., Zheng, B., Watson, R., et al. (2007). differential combining for acquiring weak GPS signals. Signal Processing, 87(5), 824–840.

    Article  Google Scholar 

  13. Li, X., & Guo, W. (2013). Efficient differential coherent accumulation algorithm for weak GPS signal bit synchronization. IEEE Communications Letters, 17(5), 936–939.

    Article  Google Scholar 

  14. Esteves, P., Sahmoudi, M., & Boucheret, M. L. (2016). Sensitivity characterization of differential detectors for acquisition of weak GNSS signals. IEEE Transactions on Aerospace and Electronic Systems, 52(1), 20–37.

    Article  Google Scholar 

  15. Wu, C., Xu, L., Zhang, H., et al. (2017). An improved acquisition method for GNSS in high dynamic environments: Differential acquisition based on compressed sensing theory. Navigation, 64, 23–34.

    Article  Google Scholar 

  16. Luo, Y., Zhang, L., & Hang, R. (2018). An acquisition algorithm based on FRFT for weak GNSS signals in a dynamic environment. IEEE Communications Letters, PP(99), 1.

    Google Scholar 

  17. Luo, Y., Hsu, L. T., & El-Sheimy, N. (2023). A baseband MLE for snapshot GNSS receiver using super-long-coherent correlation in a fractional Fourier domain. NAVIGATION: Journal of the Institute of Navigation, 70(3).

  18. Foucras, M., Julien, O., Macabiau, C., et al. (2016). Probability of detection for GNSS signals with sign transitions. IEEE Transactions on Aerospace and Electronic Systems, 52(3), 1296–1308.

    Article  Google Scholar 

  19. Fan, B., Zhang, K., Qin, Y., et al. (2013). Discrete chirp-Fourier transform-based acquisition algorithm for weak global positioning system L5 signals in high dynamic environments. Radar Sonar and Navigation IET, 7(7), 736–746.

    Article  Google Scholar 

  20. Wu, C., Xu, L. P., Zhang, H., et al. (2015). A block zero-padding method based on DCFT for L1 parameter estimations in weak signal and high dynamic environments. Frontiers of Information Technology and Electronic Engineering, 16(9), 796–804.

    Article  Google Scholar 

  21. Simon, M. K. (2006). Probability distributions involving Gaussian random variables. Springer.

    Google Scholar 

  22. Tang, P., & Wang, S. (2017). A low-complexity algorithm for fast acquisition of weak DSSS signal in high dynamic environment. GPS Solution, 21(7), 1–15.

    Google Scholar 

Download references

Acknowledgements

Not applicable.

Funding

This work was supported by Key Laboratory of Cognitive Radio and Information Processing, Ministry of Education (Guilin University of Electronic Technology) No.: CRKL220207, the National Natural Science Foundation of China under Grant 61901154 and Zhejiang Province Science Foundation for Youths under Grant LQ19F010006.

Author information

Authors and Affiliations

  1. School of Communication Engineering, Hangzhou Dianzi University, Hangzhou, 310018, Zhejiang, China

    Chao Wu

  2. Key Laboratory of Cognitive Radio and Information Processing, Guilin University of Electronic Technology, Guilin, 541004, Guangxi, China

    Chao Wu

Authors
  1. Chao Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors made contributions in the discussions, analyses, and implementation of the proposed method solution.

Corresponding author

Correspondence to Chao Wu.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Derivation of Doppler Rate Resolution

Appendix: Derivation of Doppler Rate Resolution

Based on (10), \({\boldsymbol{\Delta }}_{\boldsymbol{\alpha }}=\frac{1}{{{\varvec{N}}}_{{\varvec{B}}0}{{\varvec{T}}}_{{\varvec{s}}}}\) represents Doppler rate resolution, and when \(\left|{\boldsymbol{\alpha }}_{{\varvec{k}}}\right|\le \frac{{\boldsymbol{\Delta }}_{\boldsymbol{\alpha }}}{2}\) in (12), the correct unit corresponding to Doppler rate should be detected. In order not to cause too much attenuation of the detected peak,

$$20\mathit{lg}\left|\mathit{sin}c\left(\pi \frac{{N}_{B}{T}_{s}}{{N}_{B0}}{N}_{B}\right)\mathit{sin}c\left(\pi \frac{{N}_{B}{T}_{s}}{{N}_{B0}}{N}_{B}{N}_{SB}\right)\right|\ge -6\hspace{0.33em}dB$$
(33)

So

$$\left|\mathit{sin}c\left(\pi \frac{{N}_{B}{T}_{s}}{{N}_{B0}}{N}_{B}\right)\mathit{sin}c\left(\pi \frac{{N}_{B}{T}_{s}}{{N}_{B0}}{N}_{B}{N}_{SB}\right)\right|\ge 0.5$$
(34)

Since \(\left|{\varvec{sin}}{\varvec{c}}\left({\varvec{\pi}}\frac{{{\varvec{N}}}_{{\varvec{B}}}{{\varvec{T}}}_{{\varvec{s}}}}{{{\varvec{N}}}_{{\varvec{B}}0}}{{\varvec{N}}}_{{\varvec{B}}}\right)\right|\ge \left|{\varvec{sin}}{\varvec{c}}\left({\varvec{\pi}}\frac{{{\varvec{N}}}_{{\varvec{B}}}{{\varvec{T}}}_{{\varvec{s}}}}{{{\varvec{N}}}_{{\varvec{B}}0}}{{\varvec{N}}}_{{\varvec{B}}}{{\varvec{N}}}_{{\varvec{S}}{\varvec{B}}}\right)\right|\), (34) can be simplified further as:

$$\left|\mathit{sin}c\left(\pi \frac{{N}_{B}{T}_{s}}{{N}_{B0}}{N}_{B}{N}_{SB}\right)\right|\ge \frac{1}{\sqrt{2}}$$
(35)

So based on Taylor expansion, (35) can be simplified further as:

$$\mathit{sin}\left(\pi \frac{{N}_{B}^{2}{N}_{SB}{T}_{s}}{{N}_{B0}}\right)\approx \left(\pi \frac{{N}_{B}^{2}{N}_{SB}{T}_{s}}{{N}_{B0}}\right)-\frac{{\left(\pi \frac{{N}_{B}^{2}{N}_{SB}{T}_{s}}{{N}_{B0}}\right)}^{3}}{6}\ge \frac{1}{\sqrt{2}}\pi \frac{{N}_{B}^{2}{N}_{SB}{T}_{s}}{{N}_{B0}}$$
(36)

When \({N}_{B}\)=20,

$${N}_{B0}\ge \frac{\pi {N}_{B}^{2}{N}_{SB}{T}_{s}}{\sqrt{6\left(1-\frac{1}{\sqrt{2}}\right)}}\approx {N}_{SB}$$
(37)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, C. Low-Computation GNSS Acquisition Method for Sparse Doppler Frequency Hypotheses in High-Dynamic Environment. Wireless Pers Commun 135, 1947–1963 (2024). https://doi.org/10.1007/s11277-024-10967-x

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-024-10967-x

Keywords

Search

Navigation