Skip to main content

Advertisement

SpringerLink
Log in

System Performance Analysis in Cognitive Radio-Aided NOMA Network: An Application to Vehicle-to-Everything Communications

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

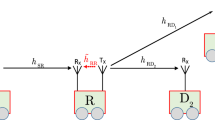
In this study, non-orthogonal multiple access (NOMA) together with cognitive radio (CR) benefit to the vehicle-to-everything (V2X) as promising application with high spectrum efficiency. We have higher priority to evaluate system performance of the secondary network in such CR-NOMA system operating in the context of V2X. We first arrange vehicles belonging to serving group in this CR-NOMA assisted V2X, and it is beneficial to serve massive connections for vehicles. There are two scenarios studied in this paper, with and without the support of CR scheme. In our proposed system, two system metrics need be investigated to evaluate performance of vehicles that need higher quality of service (QoS). Our results indicate that the outage performance gap among two vehicles exists since different transmit power allocation factors were assigned to them. In particular, the outage probability is first derived in exact forms and then the bit error rate (BER) can be further achieved. In specific situations, the optimal outage probability can be obtained by numerical simulations. Simulation results are also provided to verify the correctness of the derived expressions and it exhibits advantages of the proposed CR-NOMA assisted V2X system in terms of two main metrics such as outage probability and BER.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. IMT traffic estimates for the years 2020 to 2030, ITU-R Radiocommun. Sector ITU, Rep. ITU-R M. 2370-0, Jul. 2015.

  2. Asad, M., Basit, A., Qaisar, S., & Ali, M. Beyond 5G: Hybrid end-to-end quality of service provisioning in heterogeneous IoT networks. IEEE Access. https://doi.org/10.1109/ACCESS.2020.3032704.

  3. Li, B., Fei, Z., & Zhang, Y. (2019). UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet of Things Journal, 6(2), 2241–2263.

    Article  Google Scholar 

  4. Saad, W., Bennis, M., & Chen, M. (2019). A vision of 6G wireless systems: Applications, trends, technologies, and open research problems, [Online]. Available: arXiv:1902.10265.

  5. Do, D.-T., & Le, A.-T. (2019). NOMA based cognitive relaying: Transceiver hardware impairments, relay selection policies and outage performance comparison. Computer Communications, 146, 144–154.

    Article  Google Scholar 

  6. Do, D.-T., Van Nguyen, M.-S., Hoang, T.-A., & Lee, Byung M. (2019). Exploiting joint base station equipped multiple antenna and full-duplex D2D users in power domain division based multiple access networks. Sensors, 19(11), 2475.

    Article  Google Scholar 

  7. Li X. et al. Cooperative wireless-powered noma relaying for B5G IoT networks with hardware impairments and channel estimation errors. IEEE Internet of Things Journal. https://doi.org/10.1109/JIOT.2020.3029754.

  8. Li, X., Wang, Q., Liu, Y., Tsiftsis, T. A., Ding, Z., & Nallanathan, A. (2020). UAV-aided multi-way NOMA networks with residual hardware impairments. IEEE Wireless Communications Letters, 9(9), 1538–1542.

    Article  Google Scholar 

  9. Do, D.-T., Nguyen, M. V., Jameel, F., Jäntti, R., & Ansari, I. S. (2020). Performance evaluation of relay-aided CR-NOMA for beyond 5G communications. IEEE Access, 8, 134838–134855.

    Article  Google Scholar 

  10. Do, D.-T., Nguyen, T.-L., Rabie, K. M., Li, X., & Lee, B. M. (2020). Throughput analysis of multipair two-way replaying networks with NOMA and imperfect CSI. IEEE Access, 8, 128942–128953.

    Article  Google Scholar 

  11. Kieu, T. N., Do, D.-T., Xuan, X. N., Nhat, T. N., Duy, H. H. (2016). Wireless information and power transfer for full duplex relaying networks: Performance analysis. In Proceedings of AETA 2015: Recent Advances in Electrical Engineering and Related Sciences. Lecture Notes in Electrical Engineering, vol 371 “Wireless Information and Power Transfer for Full Duplex Relaying Networks: Performance Analysis.

  12. Islam, S. M. R., Zeng, M., Dobre, O. A., & Kwak, K.-S. (2018). Resource allocation for downlink NOMA Systems: Key techniques and open issues. IEEE Wireless Communication, 25(2), 40–47.

    Article  Google Scholar 

  13. Yan, X., Xiao, H., An, K., Zheng, G., & Chatzinotas, S. (2020). Ergodic capacity of NOMA-based uplink satellite networks with randomly deployed users. IEEE Systems Journal, 14(3), 3343–3350.

    Article  Google Scholar 

  14. Do, Dinh-Thuan., Le, A., & Lee, B. M. (2020). NOMA in cooperative underlay cognitive radio networks under imperfect SIC. IEEE Access, 8, 86180–86195.

    Article  Google Scholar 

  15. Do, D.-T., Le, A.-T., Le, C.-B., & Lee, B. M. (2019). On exact outage and throughput performance of cognitive radio based non-orthogonal multiple access networks with and without D2D link. Sensors (Basel), 19(15), 3314.

    Article  Google Scholar 

  16. Liu, X., Jia, M., Na, Z., Lu, W., & Li, F. (2018). Multi-modal cooperative spectrum sensing based on dempster-shafer fusion in 5G-based cognitive radio. IEEE Access, 6, 199–208.

    Article  Google Scholar 

  17. Liu, X., Zhang, X., Jia, M., Fan, L., Lu, W., & Zhai, X. (2018). 5G-based green broadband communication system design with simultaneous wireless information and power transfer. Physical Communication, 28, 130–137.

    Article  Google Scholar 

  18. Bariah, L., Muhaidat, S., & Al-Dweik, A. (2020). Error performance of NOMA-based cognitive radio networks with partial relay selection and interference power constraints. IEEE Transactions on Communications, 68(2), 765–777.

    Article  Google Scholar 

  19. Arzykulov, S., Nauryzbayev, G., Tsiftsis, T. A., & Maham, B. (2019). Performance analysis of underlay cognitive radio nonorthogonal multiple access networks. IEEE Transactions on Vehicular Technology, 68(9), 9318–9322.

    Article  Google Scholar 

  20. Liang, Y.-C., Zeng, Y., Peh, E. C. Y., & Hoang, A. T. (2008). Sensing-throughput tradeoff for cognitive radio networks. IEEE Transactions on Wireless Communications, 7(4), 1326–1337. https://doi.org/10.1109/TWC.2008.060869.

    Article  Google Scholar 

  21. Liu, X., Jia, M., Zhang, X., & Lu, W. (2019). A novel multichannel Internet of Things based on dynamic spectrum sharing in 5G communication. IEEE Internet Things Journal, 6(4), 5962–5970.

    Article  Google Scholar 

  22. Ligo, A. K., & Peha, J. M. (2019). Spectrum for V2X: Allocation and sharing. IEEE Transactions on Cognitive Communications and Networking, 5(3), 768–779.

    Article  Google Scholar 

  23. Xiao H. et al. Energy-efficient resource allocation in radio-frequency-powered cognitive radio network for connected vehicles. IEEE Transactions on Intelligent Transportation Systems. https://doi.org/10.1109/TITS.2020.3026746.

  24. Zhou, F., Wu, Y., Liang, Y.-C., Li, Z., Wang, Y., & Wong, K.-K. (2018). State of the art, taxonomy, and open issues on cognitive radio networks with NOMA. IEEE Wireless Communication, 25(2), 100–108.

    Article  Google Scholar 

  25. Men, J., Ge, J., & Zhang, C. (2017). Performance analysis of nonorthogonal multiple access for relaying networks over Nakagami-m fading channels. IEEE Transactions on Vehicular Technology, 66(2), 1200–1208.

    Article  Google Scholar 

  26. Lv, L., Chen, J., Ni, Q., & Ding, Z. (2017). Design of cooperative non-orthogonal multicast cognitive multiple access for 5G systems: User scheduling and performance analysis. IEEE Transactions on Communications, 65(6), 2641–2656.

    Article  Google Scholar 

  27. Lv, L., Yang, L., Jiang, H., Luan, T. H., & Chen, J. (2018). When NOMA meets multiuser cognitive radio: Opportunistic cooperation and user scheduling. IEEE Transactions on Vehicular Technology, 67(7), 6679–6684.

    Article  Google Scholar 

  28. Arzykulov, S., Nauryzbayev, G., Tsiftsis, T. A., & Maham, B. (2019). Performance analysis of underlay cognitive radio non-orthogonal multiple access networks. IEEE Transactions on Vehicular Technology, 68(9), 9318–9322.

    Article  Google Scholar 

  29. Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series and products (6th ed.). New York, NY, USA: Academic Press.

    MATH  Google Scholar 

  30. Im, G., & Lee, J. H. (2019). Outage probability for cooperative NOMA systems with imperfect SIC in cognitive radio networks. IEEE Communications Letters, 23(4), 692–695.

    Article  Google Scholar 

  31. Ji, B., Li, Y., Zhou, B., Li, C., Song, K., & Wen, H. (2019). Performance analysis of UAV relay assisted IoT communication network enhanced with energy harvesting. IEEE Access, 7, 38738–38747.

    Article  Google Scholar 

  32. Abramowitz, M., & Stegun, I. A. (1972). Handbook of mathematical functions with formulas, graphs, and mathematical tables. New York, NY, USA: Dover.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Electronics Technology, Industrial University of Ho Chi Minh City (IUH), Ho Chi Minh City, 700000, Vietnam

    Chi-Bao Le

  2. Department of Computer Science and Information Engineering, Asia University, Taichung, 41354, Taiwan

    Dinh-Thuan Do

  3. Department of Electrical and Computer Engineering, Aristotle University of Thessaloniki, 54124, Thessaloniki, Greece

    Zaharias D. Zaharis

  4. Department of Computer Science, University of Nicosia, Nicosia, Cyprus

    Constandinos X. Mavromoustakis

  5. Department of Electrical and Computer Engineering, Hellenic Mediterranean University, 71500, Estavromenos, Heraklion, Greece

    George Mastorakis & Evangelos K. Markakis

Authors
  1. Chi-Bao Le
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dinh-Thuan Do
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zaharias D. Zaharis
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Constandinos X. Mavromoustakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. George Mastorakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Evangelos K. Markakis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dinh-Thuan Do.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

In (8) we have \(P_1\) is calculated

$$\begin{aligned} \begin{aligned} {P_1}&= 1 - \underbrace{\Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2} \ge {{\bar{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}{{\left| {{h_{C{D_1}}}} \right| }^2} + 1} \right) ,{{\left| {{h_{SP}}} \right| }^2} < \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) }_{{A_1}}\\&\quad - \underbrace{\Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2} \ge {{\tilde{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}{{\left| {{h_{C{D_1}}}} \right| }^2}{{\left| {{h_{SP}}} \right| }^2} + {{\left| {{h_{SP}}} \right| }^2}} \right) ,{{\left| {{h_{SP}}} \right| }^2} > \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) }_{{A_2}}, \end{aligned} \end{aligned}$$
(33)

where \({{\bar{\chi }} _{max}} = \max \left( {\frac{{{\varepsilon _2}}}{{{\rho _{RSU}}\left[ {\alpha - {\varepsilon _2}\left( {1 - \alpha } \right) } \right] }},\frac{{{\varepsilon _1}}}{{\left( {1 - \alpha } \right) {\rho _{RSU}}}}} \right)\) and \({{\tilde{\chi }} _{max}} = \max \left( {\frac{{{\varepsilon _2}}}{{{\rho _Q}\left[ {\alpha - {\varepsilon _2}\left( {1 - \alpha } \right) } \right] }},\frac{{{\varepsilon _1}}}{{{\rho _Q}\left( {1 - \alpha } \right) }}} \right)\)

The outage probability of fist term and second terms (33) can be obtained as \({A_1}\) and \({A_2}\), respectively in following proposition.

\({A_1}\) can be calculate as

$$\begin{aligned} \begin{aligned} {A_1} =&\Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2} \ge {{\bar{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}{{\left| {{h_{C{D_1}}}} \right| }^2} + 1} \right) ,{{\left| {{h_{SP}}} \right| }^2} < \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) \\ =&\int \limits _0^{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( x \right) } \int \limits _0^\infty {{f_{{{\left| {{h_{C{D_1}}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_1}}}} \right| }^2}}}\left( {{{\bar{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}y + 1} \right) } \right) } \right] dxdy\\ =&\frac{{{e^{ - \frac{{{{\bar{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}}}}}{{{\Omega _{{h_{SP}}}}{\Omega _{{h_{C{D_1}}}}}}}\int \limits _0^{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} {{e^{ - \frac{x}{{{\Omega _{{h_{SP}}}}}}}}} \int \limits _0^\infty {{e^{ - y\left( {\frac{1}{{{\Omega _{{h_{C{D_1}}}}}}} + \frac{{\kappa {{\bar{\chi }} _{max}}{\rho _{CUE}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}} dxdy\\ =&\left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{\bar{\rho }}_{RSU}}}}}}} \right) \frac{{{\Omega _{{h_{S{D_1}}}}}{e^{ - \frac{{{{\bar{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}}}}}{{\left( {{\Omega _{{h_{S{D_1}}}}} + {\Omega _{{h_{C{D_1}}}}}\kappa {\bar{\chi }_{max}}{\rho _{CUE}}} \right) }}. \end{aligned} \end{aligned}$$
(34)

Similarly, \({A_2}\) can be expressed as

$$\begin{aligned} \begin{aligned} {A_2} =&\Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2} \ge {{\tilde{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}{{\left| {{h_{C{D_1}}}} \right| }^2}{{\left| {{h_{SP}}} \right| }^2} + {{\left| {{h_{SP}}} \right| }^2}} \right) ,{{\left| {{h_{SP}}} \right| }^2} > \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) \\ =&\int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( x \right) } \int \limits _0^\infty {{f_{{{\left| {{h_{C{D_1}}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_1}}}} \right| }^2}}}\left( {{{\tilde{\chi }} _{max}}\left( {\kappa {\rho _{CUE}}yx + x} \right) } \right) } \right] dxdy\\ =&\frac{1}{{{\Omega _{{h_{SP}}}}{\Omega _{{h_{C{D_1}}}}}}}\int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {{e^{ - x\left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}} \int \limits _0^\infty {{e^{ - y\left( {\frac{1}{{{\Omega _{{h_{C{D_1}}}}}}} + \frac{{\kappa {{\tilde{\chi }} _{max}}{\rho _{CUE}}x}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}} dxdy\\ =&\frac{{{\Omega _{{h_{S{D_1}}}}}}}{{{\Omega _{{h_{SP}}}}}}\int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {\frac{{{e^{ - x\left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}}}{{\left( {{\Omega _{{h_{S{D_1}}}}} + {\Omega _{{h_{C{D_1}}}}}\kappa {{\tilde{\chi }} _{max}}{\rho _{CUE}}x} \right) }}} dx\\ =&\frac{\zeta }{{{\Omega _{{h_{SP}}}}}}\int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {\frac{{{e^{ - x\left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}}}{{ {\zeta + x} }}} dx, \end{aligned} \end{aligned}$$
(35)

where \(\zeta = \frac{{{\Omega _{{h_{S{D_1}}}}}}}{{{\Omega _{{h_{C{D_1}}}}}\kappa {{\tilde{\chi }} _{max}}{\rho _{CUE}}}}\).

We using [29, Eq.(3.352.2)], \({A_2}\) is given as

$$\begin{aligned} \begin{aligned} {A_2} =&\frac{\zeta }{{{\Omega _{{h_{SP}}}}}}\int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {\frac{{{e^{ - x\left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}}}{{ {\zeta + x} }}} dx\\ =&- \frac{\zeta }{{{\Omega _{{h_{SP}}}}}}{e^{\zeta \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}Ei\left( { - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) \left( {\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}} + \zeta } \right) } \right) , \end{aligned} \end{aligned}$$
(36)

where \(Ei\left( . \right)\) is exponential integral function.

Substituting (36) and (34) into (33), \({P_1}\) is given by

$$\begin{aligned} \begin{aligned} {P_1} =&1 - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) \frac{{{\Omega _{{h_{S{D_1}}}}}{e^{ - \frac{{{{\bar{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}}}}}{{\left( {{\Omega _{{h_{S{D_1}}}}} + {\Omega _{{h_{C{D_1}}}}}\kappa {{\bar{\chi }} _{max}}{\rho _{CUE}}} \right) }}\\ +&\frac{\zeta }{{{\Omega _{{h_{SP}}}}}}{e^{\zeta \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) }}Ei\left( { - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\tilde{\chi }} _{max}}}}{{{\Omega _{{h_{S{D_1}}}}}}}} \right) \left( {\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}} + \zeta } \right) } \right) . \end{aligned} \end{aligned}$$
(37)

The proposition 1 is completed.

Appendix B

In (20), we have \({F_X}\left( x \right)\) of \(P_{{D_1}}^{BER}\) calculated as

$$\begin{aligned} \begin{aligned} {F_X}\left( x \right) =&1 - \Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2}> \frac{{{\mu _1}}x}{{\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}},{{\left| {{h_{SP}}} \right| }^2} < \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) \\&- \Pr \left( {{{\left| {{h_{S{D_1}}}} \right| }^2}> \frac{{{\mu _1}{{\left| {{h_{SP}}} \right| }^2}x}}{{\left( {1 - \alpha } \right) {\rho _Q}}},{{\left| {{h_{SP}}} \right| }^2} > \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} \right) \\ =&1 - \int \limits _0^{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_1}}}} \right| }^2}}}\left( {\frac{{{\mu _1}x}}{{\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}}} \right) } \right] dy\\&- \int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_1}}}} \right| }^2}}}\left( {\frac{{{\mu _1}yx}}{{\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}}} \right) } \right] dy\\ =&1 - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) {e^{ - \frac{{{\mu _1}x}}{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}}}}\\&- \frac{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{\bar{\rho }}_{RSU}}{e^{ - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{\mu _1}x}}{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}}} \right) \frac{{{\rho _Q}}}{{{{\bar{\rho }}_{RSU}}}}}}}}{{\left( {{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}} + {\mu _1}{\Omega _{{h_{SP}}}}x} \right) }}, \end{aligned} \end{aligned}$$
(38)

Substituting (38) into (20), the BER of \(D_1\) is written as

$$\begin{aligned} \begin{aligned} P_{{D_1}}^{BER} =&\frac{{\sqrt{{\bar{b}}} }}{{2\sqrt{2\pi } }}\left[ {\int \limits _0^\infty {\frac{{{e^{ - \frac{{{\bar{b}}}}{2}x}}}}{{\sqrt{x} }}} dx - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) \int \limits _0^\infty {\frac{{{e^{ - \psi x}}}}{{\sqrt{x} }}dx} } \right. \\&\left. { - \Phi {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}\int \limits _0^\infty {\frac{{{e^{ - \xi x}}}}{{\left( {\Phi + x} \right) \sqrt{x} }}} dx} \right] , \end{aligned} \end{aligned}$$
(39)

where \(\Phi = \frac{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{{\bar{\rho }} }_{RSU}}}}{{{\mu _1}{\Omega _{{h_{SP}}}}}}\), \(\psi = \left( {\frac{{{\bar{b}}}}{2} + \frac{{{\mu _1}}}{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {{\bar{\rho }}_{RSU}}}}} \right)\) and \(\xi = \left( {\frac{{{\bar{b}}}}{2} + \frac{{{\mu _1}{\rho _Q}}}{{{\Omega _{{h_{S{D_1}}}}}\left( {1 - \alpha } \right) {\bar{\rho }} _{RSU}^2}}} \right)\)

Based on [29, Eq. (3.361.2)], [29, Eq. (3.383.10)] and after few steps, (39) can then be further derived as

$$\begin{aligned} \begin{aligned} P_{{D_1}}^{BER} =&\frac{{\sqrt{{\bar{b}}} }}{{2\sqrt{2\pi } }}\left[ {\sqrt{\frac{{2\pi }}{{{\bar{b}}}}} - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) \sqrt{\frac{\pi }{\psi }} } \right. \\&\left. { - \sqrt{\Phi }{e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}} + \xi \Phi }}\Gamma \left( {\frac{1}{2}} \right) \Gamma \left( {\frac{1}{2},\xi \Phi } \right) } \right] , \end{aligned} \end{aligned}$$
(40)

where \(\Gamma \left( . \right)\) is the Gamma function and \(\Gamma \left( {.,.} \right)\) is the upper incomplete Gamma function

The proposition 2 is completed.

Appendix C

Similar to (22), we have

$$\begin{aligned} \begin{aligned} {F_Y}\left( x \right)&= 1 - \int \limits _0^{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}} {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_2}}}} \right| }^2}}}\left( {\frac{{x{\mu _2}}}{{{{{\bar{\rho }} }_{RSU}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}} \right) } \right] dx\\&\quad - \int \limits _{\frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}^\infty {{f_{{{\left| {{h_{SP}}} \right| }^2}}}\left( y \right) } \left[ {1 - {F_{{{\left| {{h_{S{D_2}}}} \right| }^2}}}\left( {\frac{{xy{\mu _2}}}{{{\rho _Q}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}} \right) } \right] dx\\&= 1 - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) {e^{ - \frac{{x{\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{{{\bar{\rho }} }_{RSU}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}}}\\&\quad - \frac{{{{\mathcal {X}}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}{{\left( {{{\mathcal {X}}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) + x} \right) }}{e^{ - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{x{\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{\rho _Q}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}} \right) \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}}dx, \end{aligned} \end{aligned}$$
(41)

where \({{\mathcal {X}}} = \frac{{{\Omega _{{h_{S{D_2}}}}}{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{\mu _2}}}\)

Substituting (41) into (22), \(P_{{D_2}}^{BER}\) is given by

$$\begin{aligned} \begin{aligned} P_{{D_2}}^{BER}&=\frac{{\sqrt{{\bar{b}}} }}{{2\sqrt{2\pi } }}\left[ {\int \limits _0^{\frac{\alpha }{{1 - \alpha }}} {\frac{{{e^{ - \frac{{{\bar{b}}}}{2}x}}}}{{\sqrt{x} }}} dx - \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right) } \right. \\&\quad \times \int \limits _0^{\frac{\alpha }{{1 - \alpha }}} {\frac{{{e^{ - \frac{{{\bar{b}}}}{2}x}}}}{{\sqrt{x} }}{e^{ - \frac{{x{\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{{{\bar{\rho }} }_{RSU}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}}}dx} - \int \limits _0^{\frac{\alpha }{{1 - \alpha }}} {\frac{{{e^{ - \frac{{{\bar{b}}}}{2}x}}}}{{\sqrt{x} }}} dx\\&\quad \left. { \times {e^{ - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{x{\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{\rho _Q}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}} \right) \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}}\frac{{{{\mathcal {X}}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) }}{{\left( {{{\mathcal {X}}}\left( {\alpha - x\left( {1 - \alpha } \right) } \right) + x} \right) }}} \right] , \end{aligned} \end{aligned}$$
(42)

The first integral in (42) can be easily obtained as in [29, Eq. (3.361.1)]. For the second integral, setting \(t = \frac{{2\left( {1 - \alpha } \right) x}}{\alpha }\) results in \(x = \frac{{\alpha \left( {t + 1} \right) }}{{2\left( {1 - \alpha } \right) }}\). Hence, (42) is given as

$$\begin{aligned} \begin{array}{l} P_{{D_2}}^{BER} = \frac{{\sqrt{{\bar{b}}} }}{{2\sqrt{2\pi } }}\left[ {\sqrt{\frac{{2\pi }}{{{\bar{b}}}}} \Phi \left( {\sqrt{\frac{{\alpha {\bar{b}}}}{{2\left( {1 - \alpha } \right) }}} } \right) - \frac{{\phi \alpha }}{{2\left( {1 - \alpha } \right) }}\int \limits _{ - 1}^1 {\frac{{{e^{ - \frac{{{\bar{b}}{{\mathcal {S}}}\left( t \right) }}{2} - \frac{{{{\mathcal {S}}}\left( t \right) {\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{{{\bar{\rho }} }_{RSU}}\left( {\alpha - {{\mathcal {S}}}\left( t \right) \left( {1 - \alpha } \right) } \right) }}}}}}{{\sqrt{{{\mathcal {S}}}\left( t \right) } }}dt} } \right. \\ \left. { - \frac{\alpha }{{2\left( {1 - \alpha } \right) }}\int \limits _{ - 1}^1 {\frac{{{{\mathcal {X}}}\left( {\alpha - {{\mathcal {S}}}\left( t \right) \left( {1 - \alpha } \right) } \right) {e^{ - \frac{{{\bar{b}}{{\mathcal {S}}}\left( t \right) }}{2} - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\mathcal {S}}}\left( t \right) {\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{\rho _Q}\left( {\alpha - {{\mathcal {S}}}\left( t \right) \left( {1 - \alpha } \right) } \right) }}} \right) \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}}}}{{\left[ {\mathcal{X}\left( {\alpha - {{\mathcal {S}}}\left( t \right) \left( {1 - \alpha } \right) } \right) + {{\mathcal {S}}}\left( t \right) } \right] \sqrt{\mathcal{S}\left( t \right) } }}} dt} \right] , \end{array} \end{aligned}$$
(43)

where \(\phi = \left( {1 - {e^{ - \frac{{{\rho _Q}}}{{{\Omega _{{h_{SP}}}}{{{\bar{\rho }} }_{RSU}}}}}}} \right)\), \({{\mathcal {S}}}\left( t \right) = \frac{{\alpha \left( {t + 1} \right) }}{{2\left( {1 - \alpha } \right) }}\) and \(\Phi \left( . \right)\) is the Error function [29, Eq. (3.321.1)]

Using the Gaussian-Chebyshev quadrature method in [32], we can obtain \(P_{{D_2}}^{BER}\) as

$$\begin{aligned} \begin{aligned} P_{{D_2}}^{BER} \approx&\frac{{\sqrt{{\bar{b}}} }}{{2\sqrt{2\pi } }}\left[ {\sqrt{\frac{{2\pi }}{{{\bar{b}}}}} \Phi \left( {\sqrt{\frac{{\alpha {\bar{b}}}}{{2\left( {1 - \alpha } \right) }}} } \right) - \phi \sum \limits _{t = 1}^T {\frac{{\pi \alpha \sqrt{1 - \varphi _t^2} }}{{2T\left( {1 - \alpha } \right) \sqrt{{{\mathcal {S}}}\left( {{\varphi _t}} \right) } }}} } \right. \\&\times {e^{ - {{\mathcal {S}}}\left( {{\varphi _t}} \right) \left( {\frac{{{\bar{b}}}}{2} + \frac{{{\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{{{\bar{\rho }} }_{RSU}}\left( {\alpha - {{\mathcal {S}}}\left( {{\varphi _t}} \right) \left( {1 - \alpha } \right) } \right) }}} \right) }} - \sum \limits _{t = 1}^T {\frac{{\pi \alpha \sqrt{1 - \varphi _t^2} {{\mathcal {X}}}}}{{2T\left( {1 - \alpha } \right) \sqrt{{{\mathcal {S}}}\left( {{\varphi _t}} \right) } }}} \\&\left. { - \frac{{\left[ {\alpha - {{\mathcal {S}}}\left( {{\varphi _t}} \right) \left( {1 - \alpha } \right) } \right] {e^{ - \frac{{\bar{b}{{\mathcal {S}}}\left( {{\varphi _t}} \right) }}{2} - \left( {\frac{1}{{{\Omega _{{h_{SP}}}}}} + \frac{{{{\mathcal {S}}}\left( {{\varphi _t}} \right) {\mu _2}}}{{{\Omega _{{h_{S{D_2}}}}}{\rho _Q}\left( {\alpha - {{\mathcal {S}}}\left( {{\varphi _t}} \right) \left( {1 - \alpha } \right) } \right) }}} \right) \frac{{{\rho _Q}}}{{{{{\bar{\rho }} }_{RSU}}}}}}}}{{\left[ {{{\mathcal {X}}}\left( {\alpha - {{\mathcal {S}}}\left( {{\varphi _t}} \right) \left( {1 - \alpha } \right) } \right) + \mathcal{S}\left( {{\varphi _t}} \right) } \right] }}} \right] , \end{aligned} \end{aligned}$$
(44)

where \({\varphi _t} = \cos \left( {\frac{{2t - 1}}{{2T}}\pi } \right)\)

The proposition 3 is completed.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Le, CB., Do, DT., Zaharis, Z.D. et al. System Performance Analysis in Cognitive Radio-Aided NOMA Network: An Application to Vehicle-to-Everything Communications. Wireless Pers Commun 120, 1975–2000 (2021). https://doi.org/10.1007/s11277-021-08273-x

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-021-08273-x

Keywords

Search

Navigation