Diversity analysis of ML and ZF detectors in physical layer network coding relay system over frequency selective channels

Abstract

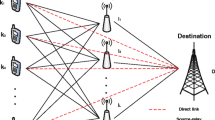
In this paper, we consider a multi-source decode and forward cooperative network coding (NC) relay system based on single-carrier zero-padded (SC-ZP) transmission scheme. All channels are L-tap frequency selective with Rayleigh fading. The cooperative maximum ratio combining (C-MRC) and the selection relaying combiners are applied and investigated at the destination, separately. We analyze the performance of proposed method in terms of symbol error probability at high signal-to-noise ratio regime, by adopting maximum likelihood (ML) and zero forcing (ZF) detectors. We prove that the considered system using the C-MRC and the ML detector, successfully exploits maximum achievable multhipath and cooperative diversity gain of 2L. To reduce the ML decoding complexity which increases with the number of sources, linear low complexity detection methods are used even though they usually do not succeed in collecting the receive diversity gain. We analytically demonstrate that proposed SC-ZP based NC system using the linear ZF detector achieves full diversity gain as like as the ML for arbitrary modulation schemes and number of sources. Moreover, an optimal NC mapping coefficients has been designed to maximize the system coding gain. Also, we extend proposed single relay NC system to multi-relay cooperative network. Single relay selection protocol is implemented based on a proposed selection criterion. In addition, simulation results illustrate that the proposed NC system employing SC-ZP technique and without need of any channel coding outperforms its competitors about 1 dB, also the processing time is reduced up to 80 percent.

Appendices

Appendix 1

To rewriting (27), first, simplification $\alpha$ from (11) yields

$$\begin{aligned} \alpha =\frac{1}{{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}}\min \,\left( \frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{1}}R}} \right\| }^{2}}}{{{\left| {{c}_{1}} \right| }^{2}}},\,...,\,\frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{M}}R}} \right\| }^{2}}}{{{\left| {{c}_{M}} \right| }^{2}}},{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}} \right) . \end{aligned}$$

(43)

According to [14], it can be show that

$$\begin{aligned} {{\left\| {{{\mathbf {H}}}_{R}}\varDelta {\mathbf {x}} \right\| }^{2}}\ge {{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}\underset{{{{\mathbf {h}}}_{RD}}\in {{{\mathbb {C}}}^{L\times 1}}}{\mathop {\inf }}\,\,\lambda _{\min _1 }^{2}\left( {{{\mathbf {{\bar{H}}}}}_{R}} \right) \triangleq {{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}{{\lambda }_{1}}, \end{aligned}$$

(44)

where ${{\lambda }_{\min _1 }}$ is the minimum singular value of ${{\mathbf {{\bar{H}}}}_{R}}\triangleq \frac{{{{\mathbf {H}}}_{R}}}{\left\| {{{\mathbf {h}}}_{RD}} \right\| }$. Same as (44), we can get

$$\begin{aligned} {{\left\| {{{\mathbf {H}}}_{S}}\varDelta {\mathbf {x}} \right\| }^{2}}\ge \underset{i=1,...,M}{\mathop {\min }}\,{{\left\| {{{\mathbf {h}}}_{{{S}_{i}}D}} \right\| }^{2}}\underset{{{{\mathbf {h}}}_{{{S}_{i}}D}}\in {{{\mathbb {C}}}^{L\times 1}}}{\mathop {\inf }}\,\,\lambda _{\min _2 }^{2}\left( {{{\mathbf {{\bar{H}}}}}_{S}} \right) \triangleq \underset{i=1,...,M}{\mathop {\min }}\,{{\left\| {{{\mathbf {h}}}_{{{S}_{i}}D}} \right\| }^{2}}{{\lambda }_{2}}, \end{aligned}$$

(45)

where ${{\lambda }_{\min _2 }}$ is the minimum singular value of ${{\mathbf {{\bar{H}}}}_{S}}\triangleq \frac{{{{\mathbf {H}}}_{S}}}{\underset{i=1,...,M}{\mathop {\min }}\,{{\left\| {{{\mathbf {h}}}_{{{S}_{i}}D}} \right\| }^{2}}}$. Substituting (44) and (45) in (26), we conclude that

$$\begin{aligned} \begin{aligned}&{{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}},\varDelta {{{\mathbf {x}}}_{R}}=0}}\left( {\mathbf {x}}\rightarrow {\mathbf {x}}+\varDelta {\mathbf {x}} \right) \le \\&Q\left( \frac{\sqrt{\rho }}{2}\sqrt{{{\lambda }_{1}}\min \left( \frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{1}}R}} \right\| }^{2}}}{{{\left| {{c}_{1}} \right| }^{2}}},...,\frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{M}}R}} \right\| }^{2}}}{{{\left| {{c}_{M}} \right| }^{2}}},{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}} \right) +{{\lambda }_{2}}\min \left( {{\left\| {{{\mathbf {h}}}_{{{S}_{1}}D}} \right\| }^{2}},...,{{\left\| {{{\mathbf {h}}}_{{{S}_{M}}D}} \right\| }^{2}} \right) } \right) . \\ \end{aligned} \end{aligned}$$

(46)

As mentioned before, all channels are frequency selective with Rayleigh fading and the L channel coefficients are denoted by the vector ${{{\mathbf {h}}}_{UV}}$, where $U\in \left\{ S,R \right\}$ and $V\in \left\{ R,D \right\}$, are i.i.d as $CN\left( 0,\sigma _{UV}^{2} \right)$. Therefor we have $\frac{{{{\mathbf {h}}}_{UV}}}{\sigma _{UV}^{2}}\sim CN\left( 0,1 \right)$. By definition ${{\eta }_{UV}}\triangleq \frac{{{\left\| {{{\mathbf {h}}}_{UV}} \right\| }^{2}}}{\sigma _{UV}^{2}}$, which is chi-squared distributed with 2L degrees of freedom, i.e. ${{\eta }_{UV}}\sim \chi _{2L}^{2}$, and substituting in (46), PEP expression in the case $\varDelta {{{\mathbf {x}}}_{R}}=0$ yields

$$\begin{aligned} {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}},\varDelta {{{\mathbf {x}}}_{R}}=0}}\left( {\mathbf {x}}\rightarrow {\mathbf {x}}+\varDelta {\mathbf {x}} \right) \le Q\left( \frac{\sqrt{\rho }}{2}\sqrt{{{\lambda }_{1}}{{\phi }_{1}}+{{\lambda }_{2}}{{\phi }_{2}}} \right) , \end{aligned}$$

(47)

where defined

$$\begin{aligned} \begin{aligned}&{{\phi }_{1}}=\min \,\left( \frac{{{\eta }_{{{S}_{1}}R}}}{\frac{{{\left| {{c}_{1}} \right| }^{2}}}{\sigma _{{{S}_{1}}R}^{2}}},\,...,\,\frac{{{\eta }_{{{S}_{M}}R}}}{\frac{{{\left| {{c}_{M}} \right| }^{2}}}{\sigma _{{{S}_{M}}R}^{2}}},\frac{{{\eta }_{RD}}}{\frac{1}{\sigma _{RD}^{2}}} \right) , \,\,\, {{\phi }_{2}}=\min \,\left( \frac{{{\eta }_{{{S}_{1}}D}}}{\frac{1}{\sigma _{{{S}_{1}}D}^{2}}},\,...,\,\frac{{{\eta }_{{{S}_{M}}D}}}{\frac{1}{\sigma _{{{S}_{M}}D}^{2}}} \right) . \end{aligned} \end{aligned}$$

(48)

Based on being independent of ${{\phi }_{1}}$ and ${{\phi }_{2}}$, and using Chernoff bound, $Q\left( x \right) \le \exp \left( -\frac{{{x}^{2}}}{2} \right)$, expected value (27), follows as

$$\begin{aligned} \begin{aligned}&{{{\mathbb {E}} }_{{{\phi }_{1}},{{\phi }_{2}}}}\left\{ Q\left( \frac{\sqrt{\rho }}{2}\sqrt{{{\lambda }_{1}}{{\phi }_{1}}+{{\lambda }_{2}}{{\phi }_{2}}} \right) \right\} \le {{{\mathbb {E}} }_{{{\phi }_{1}}}}\left\{ \exp \left( -\frac{\rho {{\lambda }_{1}}{{\phi }_{1}}}{8} \right) \right\} {{{\mathbb {E}} }_{{{\phi }_{2}}}}\left\{ \exp \left( -\frac{\rho {{\lambda }_{2}}{{\phi }_{2}}}{8} \right) \right\} \\&\quad =\int \limits _{0}^{\infty }{\exp \left( -\frac{\rho {{\lambda }_{1}}{{\phi }_{1}}}{8} \right) }{{f}_{{{\phi }_{1}}}}\left( {{\phi }_{1}} \right) d{{\phi }_{1}}\int \limits _{0}^{\infty }{\exp \left( -\frac{\rho {{\lambda }_{2}}{{\phi }_{2}}}{8} \right) }{{f}_{{{\phi }_{2}}}}\left( {{\phi }_{2}} \right) d{{\phi }_{2}}\triangleq I. \\ \end{aligned} \end{aligned}$$

(49)

where ${{f}_{{{\phi }_{1}}}}\left( {{\phi }_{1}} \right)$ and ${{f}_{{{\phi }_{2}}}}\left( {{\phi }_{2}} \right)$ are the Probability Density Function (PDF) of ${{{\phi }_{1}}}$ and ${{{\phi }_{2}}}$, respectively. By changing variables ${{\varepsilon }_{1}}\triangleq \rho {{\lambda }_{1}}{{\phi }_{1}}$ and ${{\varepsilon }_{2}}\triangleq \rho {{\lambda }_{2}}{{\phi }_{2}}$ the integrals in (49) reshapes to

$$\begin{aligned} I=\int \limits _{0}^{\infty }{\exp \left( -\frac{{{\varepsilon }_{1}}}{8} \right) }{{f}_{{{\phi }_{1}}}}\left( \frac{{{\varepsilon }_{1}}}{\rho {{\lambda }_{1}}} \right) \,\frac{1}{\rho {{\lambda }_{1}}}d{{\varepsilon }_{1}}\int \limits _{0}^{\infty }{\exp \left( -\frac{{{\varepsilon }_{2}}}{8} \right) }{{f}_{{{\phi }_{2}}}}\left( \frac{{{\varepsilon }_{2}}}{\rho {{\lambda }_{2}}} \right) \,\frac{1}{\rho {{\lambda }_{2}}}d{{\varepsilon }_{2}}. \end{aligned}$$

(50)

According to (48), variables ${{{\phi }_{1}}}$ and ${{{\phi }_{2}}}$ are minimum functions. For two independent variables X and Y the variable $W=min(X,Y)$ has Cumulative Density Function (CDF) as ${{F}_{W}}(w)={{F}_{X}}(w)+{{F}_{Y}}(w)-{{F}_{X}}(w){{F}_{Y}}(w)$ [27]. Also, for M independent variables, the CDF of variable minimum function is contains from the terms belong to sum CDF of variables and the expression consisting of multiplying CDF of variables. Since we want to calculate the upper bound of PEP in high SNR values, $\left( \rho \rightarrow \infty \right)$, follows from (50), the major term under minimum variable function is sum CDF of variables. Therefore, applying the asymptotic of minimum variable function for $\left( \rho \rightarrow \infty \right)$ we get

$$\begin{aligned} \begin{aligned}&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,{{f}_{{{\phi }_{1}}}}\left( \frac{{{\varepsilon }_{1}}}{\rho {{\lambda }_{1}}} \right) =\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,\,\frac{1}{{{\lambda }_{1}}}\left( \sum \limits _{i=1}^{M}{\frac{1}{\sigma _{{{S}_{i}}D}^{2}}{{f}_{{{\eta }_{{{S}_{i}}D}}}}\left( \frac{1}{{{\lambda }_{1}}\sigma _{{{S}_{i}}D}^{2}}\left( \frac{{{\varepsilon }_{1}}}{\rho {{\lambda }_{1}}} \right) \right) } \right) , \\&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,{{f}_{{{\phi }_{2}}}}\left( \frac{{{\varepsilon }_{2}}}{\rho {{\lambda }_{2}}} \right) =\\ {}&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,\,\frac{1}{{{\lambda }_{2}}}\left( \sum \limits _{i=1}^{M}{\frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}D}^{2}}{{f}_{{{\eta }_{{{S}_{i}}R}}}}\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{{{\lambda }_{2}}\sigma _{{{S}_{i}}R}^{2}}\left( \frac{{{\varepsilon }_{2}}}{\rho {{\lambda }_{2}}} \right) \right) +\frac{1}{\sigma _{RD}^{2}}{{f}_{{{\eta }_{RD}}}}\left( \frac{1}{{{\lambda }_{2}}\sigma _{RD}^{2}}\left( \frac{{{\varepsilon }_{2}}}{\rho {{\lambda }_{2}}} \right) \right) } \right) . \\ \end{aligned} \end{aligned}$$

(51)

Based on distributions of variables ${{\eta }_{{{S}_{i}}D}}$, ${{\eta }_{{{S}_{i}}R}}$, and ${{\eta }_{{R}D}}$ are chi-squared distributed with 2L degrees of freedom as mentioned before, the asymptotic PDF of variables ${{{\phi }_{1}}}$ and ${{{\phi }_{2}}}$ in $\left( \rho \rightarrow \infty \right)$ (50), can be calculated and (51) yields

$$\begin{aligned} \begin{aligned}&{{{\mathbb {E}}}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left\{ {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}},\varDelta {{{\mathbf {x}}}_{R}}=0}}\left( {\mathbf {x}}\rightarrow {\mathbf {x}}+\varDelta {\mathbf {x}} \right) {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left( \varDelta {{{\mathbf {x}}}_{R}} \right) \right\} \\&\quad \le \left[ {{\left( \frac{1}{{{\lambda }_{1}}} \right) }^{L}}{{\left( \frac{1}{\rho } \right) }^{L}} \sum \limits _{i=1}^{M}{{{\left( \frac{1}{\sigma _{{{S}_{i}}D}^{2}} \right) }^{L}}} \right] \left[ {{\left( \frac{1}{{{\lambda }_{2}}} \right) }^{L}}{{\left( \frac{1}{\rho } \right) }^{L}}\left( \sum \limits _{i=1}^{M}{{{\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}} \right) }^{L}}+{{\left( \frac{1}{\sigma _{RD}^{2}} \right) }^{L}}} \right) \right] \\ {}&\doteq {{G}_{1}}^{-2L}{{\rho }^{-2L}}. \end{aligned} \end{aligned}$$

(52)

Appendix 2

To calculate terms of (29), first we utilize inequality ${{\left\| {{{\mathbf {H}}}_{R}}\varDelta {{{\mathbf {x}}}_{R}} \right\| }^{2}}\le {{\left\| {{{\mathbf {H}}}_{R}} \right\| }^{2}}{{\left\| \varDelta {{{\mathbf {x}}}_{R}} \right\| }^{2}}$. According to structure of matrix ${{{\mathbf {H}}}_{R}}\in {{{\mathbb {C}}}^{N\times MK}}$ (8), it consisting of M Toeplitz matrices ${{{\mathbf {H}}}_{RD}}\in {{{\mathbb {C}}}^{N\times K}}$ defined in (5) which has K columns with equal norms ${{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}$. Since $\sum \limits _{i=1}^{M}{{{\left| {{c}_{i}} \right| }^{2}}=1}$, we get

$$\begin{aligned} {{\left\| {{{\mathbf {H}}}_{R}} \right\| }^{2}}=\sum \limits _{i=1}^{M}{{{\left| {{c}_{i}} \right| }^{2}}K{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}}=K{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}, \end{aligned}$$

(53)

where $\varDelta {{{\mathbf {x}}}_{R}}\in {{{\mathbb {C}}}^{MK\times 1}}$, is the relay error vector. According to ${M}'$ points constellation, the maximum distance is ${{\left( 2\sqrt{M'} \right) }^{2}}$. So we have ${{\left\| \varDelta {{{\mathbf {x}}}_{R}} \right\| }^{2}}\le MK{{\left( 2\sqrt{M'} \right) }^{2}}$. Therefore (53) follows

$$\begin{aligned} {{\left\| {{{\mathbf {H}}}_{R}}\varDelta {{{\mathbf {x}}}_{R}} \right\| }^{2}}\le \left( K{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}} \right) \left( {{\left( 2\sqrt{{{M}'}} \right) }^{2}}MK \right) =4M{M}'{{K}^{2}}{{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}\triangleq \theta {{\left\| {{{\mathbf {h}}}_{RD}} \right\| }^{2}}. \end{aligned}$$

(54)

As mentioned in Appendix 1, we defined ${{\eta }_{{{S}_{i}}R}}\triangleq \frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{i}}R}} \right\| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}}$, which is chi-squared distributed with 2L degrees of freedom, i.e. ${{\eta }_{{{S}_{i}}R}}\sim \chi _{2L}^{2}$. Based on (54) and $\alpha$ calculated in (43), we get

$$\begin{aligned} \alpha {{\left\| {{{\mathbf {H}}}_{R}}\varDelta {{{\mathbf {x}}}_{R}} \right\| }^{2}}\le \theta \min \,\left( \frac{{{\eta }_{{{S}_{1}}R}}}{\frac{{{\left| {{c}_{1}} \right| }^{2}}}{\sigma _{{{S}_{1}}R}^{2}}},\,...,\,\frac{{{\eta }_{{{S}_{M}}R}}}{\frac{{{\left| {{c}_{M}} \right| }^{2}}}{\sigma _{{{S}_{M}}R}^{2}}},\frac{{{\eta }_{RD}}}{\frac{1}{\sigma _{RD}^{2}}} \right) \triangleq {{\varphi }_{1}}. \end{aligned}$$

(55)

According to (45) and definition of ${{\phi }_{2}}$ in (48), we get ${{\left\| {{{\mathbf {H}}}_{S}}\varDelta {\mathbf {s}} \right\| }^{2}}\ge {{\lambda }_{2}}{{\phi }_{2}}\,\triangleq {{\varphi }_{2}}$. As mentioned before, in the condition $\varDelta {{{\mathbf {x}}}_{R}}\ne 0$, we assumed the worst-case $\varDelta {{{\mathbf {x}}}_{R}}-\varDelta {\mathbf {x}}={\mathbf {0}}$. So, rewriting (28) gives

$$\begin{aligned} {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}},\varDelta {{{\mathbf {x}}}_{R}}=0}}\left( {\mathbf {x}}\rightarrow {\mathbf {x}}+\varDelta {\mathbf {x}} \right) \le Q\left( \frac{1}{2}\sqrt{\rho \frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{{{\varphi }_{2}}+{{\varphi }_{1}}}} \right) . \end{aligned}$$

(56)

Applying definition ${{\eta }_{{{S}_{i}}R}}\triangleq \frac{{{\left\| {{{\mathbf {h}}}_{{{S}_{i}}R}} \right\| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}}$ in the vector of relay error probability, an upper bound (25) in the case $\varDelta {{{\mathbf {x}}}_{R}}\ne 0$ follows as

$$\begin{aligned} \begin{aligned}&{{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left( \varDelta {{{\mathbf {x}}}_{R}} \right) \le Q\sqrt{\rho \min \,\left( \sigma _{{{S}_{1}}R}^{2}{{\eta }_{{{S}_{1}}R}},...,\,\sigma _{{{S}_{M}}R}^{2}{{\eta }_{{{S}_{M}}R}} \right) } \\&\quad \le Q\sqrt{\rho \min \left( \frac{{{\left| {{c}_{1}} \right| }^{2}}}{\sigma _{{{S}_{1}}R}^{2}},...,\frac{{{\left| {{c}_{M}} \right| }^{2}}}{\sigma _{{{S}_{M}}R}^{2}} \right) \min \,\left( \frac{\sigma _{{{S}_{1}}R}^{2}{{\eta }_{{{S}_{1}}R}}}{{{\left| {{c}_{1}} \right| }^{2}}},...,\frac{\sigma _{{{S}_{M}}R}^{2}{{\eta }_{{{S}_{M}}R}}}{{{\left| {{c}_{M}} \right| }^{2}}}, \sigma _{RD}^{2}{{\eta }_{RD}} \right) } \\&\quad \triangleq Q\sqrt{\rho {{\beta }^{2}}\frac{{{\varphi }_{1}}}{\theta }}\le \exp \left( -\frac{\rho {{\beta }^{2}}}{2\theta }{{\varphi }_{1}} \right) . \\ \end{aligned} \end{aligned}$$

(57)

The last step follows from the Chernoff bound. By the definitions (56) and to calculate upper bound on PEP in this case, following fact about Q-function utilize as

$$\begin{aligned} Q(z)\le \left\{ \begin{matrix} \exp \left( -\frac{{{z}^{2}}}{2} \right) \quad z>0 \\ 1\qquad \qquad z<0 \\ \end{matrix} \right. . \end{aligned}$$

(58)

Therefore, an upper bound on PEP can be rewritten as sum of two integrals for two conditions $z>0$ and $z<0$ which z is the variable of Q-function in (58). Also, we know that $0<{{\varphi }_{1}}<\infty$ and $0<{{\varphi }_{2}}<\infty$. So, one integral for the condition $z<0$, that is equal to $0<{{\varphi }_{2}}<{{\varphi }_{1}}$ and $0<{{\varphi }_{1}}<\infty$. The others for $z>0$ which achieves to ${{\varphi }_{1}}<{{\varphi }_{2}}<\infty$ and $0<{{\varphi }_{1}}<\infty$. Considering (56) and (57) probabilities and according to above discussion about integral bounds, upper bound on PEP in this case yields

$$\begin{aligned} \begin{aligned}&{{{\mathbb {E}} }_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left\{ Q\left( \frac{1}{2}\sqrt{\rho \frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{{{\varphi }_{2}}+{{\varphi }_{1}}}} \right) \exp \left( -\frac{\rho {{\beta }^{2}}}{2\theta }{{\varphi }_{1}} \right) \right\} \\&\quad =\int _{0}^{\infty }{\int _{0}^{{{\varphi }_{1}}}{\exp \left( -\frac{\rho {{\beta }^{2}}}{2\theta }{{\varphi }_{1}} \right) {{f}_{{{\varphi }_{1}}}}\left( {{\varphi }_{1}} \right) {{f}_{{{\varphi }_{2}}}}\left( {{\varphi }_{2}} \right) d{{\varphi }_{2}}d{{\varphi }_{1}}}} \\&\qquad +\int _{0}^{\infty }{\int _{{{\varphi }_{1}}}^{\infty }{\exp \left( -\frac{\rho }{8}\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{{{\varphi }_{2}}+{{\varphi }_{1}}} \right) \exp \left( -\frac{\rho {{\beta }^{2}}}{2\theta }{{\varphi }_{1}} \right) {{f}_{{{\varphi }_{1}}}}\left( {{\varphi }_{1}} \right) {{f}_{{{\varphi }_{2}}}}\left( {{\varphi }_{2}} \right) d{{\varphi }_{2}}d{{\varphi }_{1}}}}\\&\quad \triangleq {{I}_{1}}+{{I}_{2}} \end{aligned} \end{aligned}$$

(59)

First we calculate ${{I}_{1}}$. By changing variable $\tau \triangleq \frac{\rho {{\beta }^{2}}}{\theta }{{\varphi }_{1}}$, the integrals ${{I}_{1}}$ yields

$$\begin{aligned} \begin{aligned} {{I}_{1}}&=\int _{0}^{\infty }{\exp \left( -\frac{\rho {{\beta }^{2}}}{2\theta }{{\varphi }_{1}} \right) {{f}_{{{\varphi }_{1}}}}\left( {{\varphi }_{1}} \right) d{{\varphi }_{1}}\int _{0}^{{{\varphi }_{1}}}{{{f}_{{{\varphi }_{2}}}}\left( {{\varphi }_{2}} \right) d{{\varphi }_{2}}}} \\&=\int _{0}^{\infty }{{{F}_{{{\varphi }_{2}}}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) \exp \left( -\frac{\tau }{2} \right) {{f}_{{{\varphi }_{1}}}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) \frac{\theta }{\rho {{\beta }^{2}}}d\tau }. \end{aligned} \end{aligned}$$

(60)

As mentioned in Appendix 1, since ${{{\varphi }_{1}}}$ and ${{{\varphi }_{2}}}$ are minimum functions and we want to calculate the upper bound of PEP in $\left( \rho \rightarrow \infty \right)$, the majority term under minimum variable function is sum CDF of variables. Therefore, with the approximation of minimum variable function for $\left( \rho \rightarrow \infty \right)$ and definitions of ${{{\varphi }_{1}}}$ (55) and ${{{\varphi }_{2}}}$, their distributions follow as

$$\begin{aligned} \begin{aligned}&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,{{f}_{{{\varphi }_{1}}}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) =\\ {}&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,\,\frac{1}{\theta }\left( \sum \limits _{i=1}^{M}{\frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}D}^{2}}{{f}_{{{\eta }_{{{S}_{i}}R}}}}\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{{{\lambda }_{2}}\sigma _{{{S}_{i}}R}^{2}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) \right) +\frac{1}{\sigma _{RD}^{2}}{{f}_{{{\eta }_{RD}}}}\left( \frac{1}{{{\lambda }_{2}}\sigma _{RD}^{2}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) \right) } \right) , \\&\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,{{F}_{{{\varphi }_{2}}}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) =\underset{\rho \rightarrow \infty }{\mathop {\lim }}\,\,\left( \sum \limits _{i=1}^{M}{{{F}_{{{\eta }_{{{S}_{i}}D}}}}\left( \frac{1}{{{\lambda }_{2}}\sigma _{{{S}_{i}}D}^{2}}\left( \frac{\theta }{\rho {{\beta }^{2}}}\tau \right) \right) } \right) . \\ \end{aligned} \end{aligned}$$

(61)

The distributions of variables ${{\eta }_{{{S}_{i}}D}}$, ${{\eta }_{{{S}_{i}}R}}$ and ${{\eta }_{{R}D}}$ are chi-squared distributed with 2L degrees of freedom, as mentioned in Appendix 1. Due to approximation distributions of random variables ${{{\varphi }_{1}}}$ and ${{{\varphi }_{2}}}$ in $\left( \rho \rightarrow \infty \right)$, (61) yields

$$\begin{aligned} \begin{aligned}&{{I}_{1}}\doteq \\&\left[ {{\left( \frac{\theta }{{{\beta }^{2}}{{\lambda }_{2}}} \right) }^{L}}{{\left( \frac{1}{\rho } \right) }^{L}} \sum \limits _{i=1}^{M}{{{\left( \frac{1}{\sigma _{{{S}_{i}}D}^{2}} \right) }^{L}}} \right] \left[ {{\left( \frac{1}{{{\beta }^{2}}} \right) }^{L}}{{\left( \frac{1}{\rho } \right) }^{L}}\left( \sum \limits _{i=1}^{M}{{{\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}} \right) }^{L}}+{{\left( \frac{1}{\sigma _{RD}^{2}} \right) }^{L}}} \right) \right] . \end{aligned} \end{aligned}$$

(62)

To calculate $I_2$ defined in (59]), by changing variables ${{\zeta }_{1}}\triangleq \rho {{\varphi }_{1}}$ and ${{\zeta }_{2}}\triangleq \rho {{\varphi }_{2}}$, it follows as

$$\begin{aligned} \begin{aligned}&{{I}_{2}}=\\&{{\left( \frac{1}{\rho } \right) }^{2}}\int _{0}^{\infty }{\int _{{{\zeta }_{1}}}^{\infty }{\exp \left( -\frac{1 }{8}\frac{{{\left( {{\zeta }_{2}}-{{\zeta }_{1}} \right) }^{2}}}{{{\zeta }_{2}}+{{\zeta }_{1}}} \right) \exp \left( -\frac{{{\beta }^{2}}}{2\theta }{{\zeta }_{1}} \right) {{f}_{{{\zeta }_{1}}}}\left( \frac{{{\zeta }_{1}}}{\rho } \right) {{f}_{{{\zeta }_{2}}}}\left( \frac{{{\zeta }_{2}}}{\rho } \right) d{{\zeta }_{2}}d{{\zeta }_{1}}}}. \end{aligned} \end{aligned}$$

(63)

Similar to what was expressed about the distribution of two random variables ${{{\varphi }_{1}}}$ and ${{{\varphi }_{2}}}$ in (61), and applying for asymptotic PDFs in $I_2$ in the case $\left( \rho \rightarrow \infty \right)$, (63) yields

$$\begin{aligned} \begin{aligned}&{{I}_{2}}\doteq \left[ {{\left( \frac{1}{{{\lambda }_{2}}} \right) }^{L}}{{\left( \frac{1}{\rho } \right) }^{L}} \sum \limits _{i=1}^{M}{{{\left( \frac{1}{\sigma _{{{S}_{i}}D}^{2}} \right) }^{L}}} \right] \left[ \frac{1}{\theta }{{\left( \frac{1}{\rho } \right) }^{L}}\left( \sum \limits _{i=1}^{M}{{{\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}} \right) }^{L}}+{{\left( \frac{1}{\sigma _{RD}^{2}} \right) }^{L}}} \right) \right] \\&\quad \times \int _{0}^{\infty }{\int _{{{\zeta }_{1}}}^{\infty }{{{\zeta }_{1}}^{L-1}{{\zeta }_{2}}^{L-1}\exp \left( -\frac{1 }{8}\frac{{{\left( {{\zeta }_{2}}-{{\zeta }_{1}} \right) }^{2}}}{{{\zeta }_{2}}+{{\zeta }_{1}}} \right) \exp \left( -\frac{{{\beta }^{2}}}{2\theta }{{\zeta }_{1}} \right) d{{\zeta }_{2}}d{{\zeta }_{1}}}}. \\ \end{aligned} \end{aligned}$$

(64)

Now, to prove that $I_2$ also achieves full diversity gain 2L, just its enough to demonstrate that the double integrals in (64) for asymptotic case $\left( \rho \rightarrow \infty \right)$ is finite. By changing variables ${{\lambda }_{1}}={{\zeta }_{2}}+{{\zeta }_{1}}$ and ${{\lambda }_{2}}={{\zeta }_{2}}-{{\zeta }_{1}}$, the integral in (64) follows

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty }{\int _{0}^{{{\lambda }_{1}}}{{{\left( \frac{{{\lambda }_{1}}-{{\lambda }_{2}}}{2} \right) }^{L-1}}{{\left( \frac{{{\lambda }_{1}}+{{\lambda }_{2}}}{2} \right) }^{L-1}}}} \\&\quad \times \exp \left( -\frac{\rho }{8}\frac{{{\left( {{\lambda }_{2}} \right) }^{2}}}{{{\lambda }_{1}}} \right) \exp \left( -\frac{{{\beta }^{2}}}{4\theta }\left( {{\lambda }_{1}}-{{\lambda }_{2}} \right) \right) d{{\lambda }_{2}}d{{\lambda }_{1}} \\ \end{aligned} \end{aligned}$$

(65)

To continue, we consider the following expansions

$$\begin{aligned} \begin{aligned} {{\left( {{\lambda }_{1}}-{{\lambda }_{2}} \right) }^{L-1}}&=\sum \limits _{i=0}^{L-1}{{{\left( -1 \right) }^{i}}\left( \begin{matrix} L-1 \\ i \\ \end{matrix} \right) {{\left( {{\lambda }_{1}} \right) }^{L-1-i}}{{\left( -{{\lambda }_{2}} \right) }^{i}}}\\ {}&\le \sum \limits _{i=0,\,even}^{L-1}{{{\left( -1 \right) }^{i}}\left( \begin{matrix} L-1 \\ i \\ \end{matrix} \right) {{\left( {{\lambda }_{1}} \right) }^{L-1-i}}{{\left( -{{\lambda }_{2}} \right) }^{i}}}, \\ {{\left( {{\lambda }_{1}}+{{\lambda }_{2}} \right) }^{L-1}}&=\sum \limits _{j=0}^{L-1}{\left( \begin{matrix} L-1 \\ j \\ \end{matrix} \right) {{\left( {{\lambda }_{1}} \right) }^{L-1-j}}{{\left( {{\lambda }_{2}} \right) }^{j}}}. \end{aligned} \end{aligned}$$

(66)

Based on (66) expansions, an upper bound of (65) can be derive as

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty }{\int _{0}^{{{\lambda }_{1}}}{\sum \limits _{i=0,\,even}^{L-1}{\sum \limits _{j=0}^{L-1}{{{h}_{i,j}}{{\left( {{\lambda }_{1}} \right) }^{2(L-1)-(i+j)}}{{\left( {{\lambda }_{2}} \right) }^{(i+j)}}}}}} \\&\quad \times \exp \left( -\frac{\rho }{8}\frac{{{\left( {{\lambda }_{2}} \right) }^{2}}}{{{\lambda }_{1}}} \right) \exp \left( -\frac{{{\beta }^{2}}}{4\theta }\left( {{\lambda }_{1}}-{{\lambda }_{2}} \right) \right) d{{\lambda }_{2}}d{{\lambda }_{1}} \\ \end{aligned} \end{aligned}$$

(67)

where ${{h}_{i,j}}$ is addition function than given from succession of above expansions. By putting ${{\lambda }_{1}}>{{\lambda }_{2}}$ in the phrase $exp \left( -\frac{\rho }{8}\frac{{{\left( {{\lambda }_{2}} \right) }^{2}}}{{{\lambda }_{1}}} \right)$ and integrating towards ${{\lambda }_{2}}$, we get

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{{{\lambda }_{1}}}{{{\left( {{\lambda }_{2}} \right) }^{(i+j)}}}\exp \left( -\frac{b}{4}{{\lambda }_{2}} \right) d{{\lambda }_{2}}\\&\quad =(i+j)!{{\left( \frac{b}{4} \right) }^{-(i+j)-1}}\left[ 1-{{\exp }\left( {-\frac{b}{4}{{\lambda }_{1}}}\right) } \right] \sum \limits _{k=0}^{i+j}{\frac{{{\left( \frac{b}{4}{{\lambda }_{1}} \right) }^{k}}}{k!}}, \end{aligned} \end{aligned}$$

(68)

where $b=\frac{1}{2}-\frac{{{\beta }^{2}}}{\theta }$. By inserting (68) in (67), the upper bound of the dual integral in ${I}_{2}$ follows

$$\begin{aligned} \begin{aligned}&\sum \limits _{i=0,\,even}^{L-1}{\sum \limits _{j=0}^{L-1}{{{h}_{i,j}}}}(i+j)!{{\left( \frac{b}{4} \right) }^{-(i+j)-1}}\int \limits _{0}^{\infty }{{{\left( {{\lambda }_{1}} \right) }^{2(L-1)-(i+j)}}{{\exp }{\left( -\frac{{{\beta }^{2}}}{4\theta }{{\lambda }_{1}} \right) }}d{{\lambda }_{1}}}+ \\&\sum \limits _{i=0,\,even}^{L-1}{\sum \limits _{j=0}^{L-1}{{{h}_{i,j}}}}(i+j)!{{\left( \frac{b}{4} \right) }^{-(i+j)-1}}\int \limits _{0}^{\infty }{\sum \limits _{k=0}^{i+j}{\frac{{{\left( \frac{b}{4}{{\lambda }_{1}} \right) }^{k+2(L-1)-(i+j)}}}{k!}}{{\exp }{\left( -\frac{1}{8}{{\lambda }_{1}} \right) }}d{{\lambda }_{1}}}. \\ \end{aligned} \end{aligned}$$

(69)

It’s clear that (69) has the form of a finite-band integral. Finally, using (69) in (64) and according to the expression that was previously obtained for $I_{1}$ in (62), the expectations (59) can be calculated. Therefore, the asymptotic PEP when the relay has error(s), $\varDelta {{{\mathbf {x}}}_{R}}\ne 0$, satisfies

$$\begin{aligned} \begin{aligned}&{{{\mathbb {E}}}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left\{ {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}},\varDelta {{{\mathbf {x}}}_{R}}\ne 0}}\left( {\mathbf {x}}\rightarrow {\mathbf {x}}+\varDelta {\mathbf {x}} \right) {{P}_{{{{\mathbf {H}}}_{S}},{{{\mathbf {H}}}_{R}}}}\left( \varDelta {{{\mathbf {x}}}_{R}} \right) \right\} \\&\quad \le \left[ {{\left( \frac{1}{\rho } \right) }^{L}} \sum \limits _{i=1}^{M}{{{\left( \frac{1}{\sigma _{{{S}_{i}}D}^{2}} \right) }^{L}}} \right] \left[ {{\left( \frac{1}{\rho } \right) }^{L}}\left( \sum \limits _{i=1}^{M}{{{\left( \frac{{{\left| {{c}_{i}} \right| }^{2}}}{\sigma _{{{S}_{i}}R}^{2}} \right) }^{L}}+{{\left( \frac{1}{\sigma _{RD}^{2}} \right) }^{L}}} \right) \right] \\&\quad \doteq {{G}_{2}}^{-2L}{{\rho }^{-2L}}. \\ \end{aligned} \end{aligned}$$

(70)