1 Introduction

The increasing demand for broadband wireless communications has resulted in a number of technologies being implemented in a contemporary wireless transceiver. One of these is Massive Multiple-Input Multiple-Output (mMIMO) [1] that allows for a significant network capacity increase by utilization of multiple antennas at the Base Stations (BSs). These antennas can also be used for other purposes, e.g., to allow for signal source positioning. The availability of precise positioning information facilitates the prevalence of interactive forms of services or marketing. One may imagine possibilities like assisted sightseeing in historical areas or museums, shopping racks with proximity-based advertising or assistance in commuting. Overall, the angle-of-arrival-based positioning can be used for several services ranging from application-layer services, e.g., driving assistance or indoor positioning to improvement of network operation, e.g., using so-called Radio Environment Maps [2, 3].

One of the basic schemes for location estimation using multiple antennas is the Angle of Arrival (AoA) technique. Given a number of antenna elements spaced at regular intervals the angle of arrival can be discerned by observing differences in the phase of received signals. Angle estimation methods can be categorized into three groups: beamforming, subspace, and parametric [4]. Subspace algorithms offer a compromise solution between accuracy and computational complexity. Among subspace methods, the Root Multiple Signal Classification (Root-MUSIC) algorithm provides the most accurate results, as presented in [4]. AoA estimation accuracy greatly depends on the system’s hardware and radio conditions. The main hardware problem encountered in AoA systems is the accuracy and stability of the radio front end phase synchronization. Alignment in the frequency and time domains can be easily achieved by distributing a reference clock serving as a Phased Locked Loop (PLL) input signal and gating pulses marking specified moments in time. Due to the high scale of integration and multiple stages of signal processing or conversion, the resultant phases of end signals significantly differ among front ends in the system. Moreover, manufacturing inaccuracies and temperature dependency especially affect the phase of the signal and may further contribute to the offset. In the case of wideband or agile Radio Frequency (RF) transceivers, the issue of phase synchronization becomes even more complicated as the phase offset between RF front ends depends on the center frequency [5]. On the other hand, the radio environment can constitute a significant source of AoA error. Multi-path propagation causes a signal from a single source to arrive from many different directions. Moreover, it is possible that many signal sources will be active in the vicinity of the AoA receiver causing interference and resulting in AoA estimation error.

The introduction of Software-Defined Radio (SDR) platforms has enabled rapid system prototyping and algorithm evaluation due to the flexibility of the signal processing stage and extensive control over the radio front ends. By using SDRs, the data stream of each receiving (RX) or transmitting (TX) channel can be processed in a personal computer serving as a central hub of the system. There are several low-cost devices that enable quick AoA prototyping. In [6], a Texas Instruments development board consisting of 6 switched antennas is used in AoA estimation. Moreover, RTL-SDR modules with an additional clock distribution network can be used in this context [7]. Also, there exist some off-the-shelf solutions that consist of multiple RTL-SDR chipsets with an embedded clock distribution system [8]. Even selected Wireless Local Area Network (WLAN) access points with software modifications can be utilized to perform coarse AoA estimation [9]. Still, probably the most popular SDR devices used in prototyping and evaluation of wireless systems are the Universal Software Radio Peripherals (USRPs) produced by Ettus Research.

The popularity of SDR devices has brought about multiple publications concerning the implementation of angle-of-arrival systems in various SDRs considering numerous approaches to front end synchronization. Ettus Research has published a white paper which describes device synchronization and showcases AoA estimation with the use of an X310 device [10]. The presented one-time calibration routine consists of attaching a signal source via a splitter to all RX channels simultaneously. Then, for a short period, the phase difference between channels is measured, averaged, and saved to a file. Next, the wired setup is replaced by antennas to perform AoA measurements. The saved coefficients representing the phase shift are applied to compensate phase differences by multiplying the stream of signal samples by a complex value representing the required shift in the processing software. This approach, although simple, does not take into consideration the possible drift of the coefficient. Moreover, there is no discussion on the validity of the measured coefficient, e.g., for a different device, carrier frequency, or gain.

It is also possible to synchronize the receiving front ends without the need to reconfigure connections at RF ports. When the SDR device is equipped with RF front ends with two coherent RX channels, one may be utilized as input for the reference signal distributed with matched length cables. Such an approach was presented in [11] with the use of National Instruments USRP 2954R. In this case, the RX channel used for phase alignment is excluded from operation in the AoA estimation phase, reducing its potential performance. Moreover, it is required that both RX channels of a given front end introduce a similar phase shift. The precise estimation of the phase shift difference requires precise cables and splitters to be used. Dissimilarities between signal paths can contribute to an uncompensated accuracy error in this method. As before, an additional independent transmitter is required for synchronization. However, the calibration routine does not require any manual intervention.

The previously mentioned white paper concerning a gr-doa package was more widely discussed in [12], where different hardware implementations were described. The setup consisting of multiple USRPs N210, each with 1 RX and 1 TX channel, was presented with an unusual calibration method. The phase synchronizing tone was inserted into the TX port of the device with matched cable lengths. Due to the internal switching network between the TX antenna port and RX channel, used normally for half-duplex operation, a cross-talk occurs between both antenna ports. The tone inserted into the TX antenna port was received at the RX side without the need to connect anything to the RX port or rearrange the wiring. The authors claim that the similarity of RX and TX signal paths result in a repeatable phase shift across the device, providing sufficient calibration accuracy. It should be noted that the USRP N210 clock used in the mentioned setup produces phase ambiguity, which results in a random initial phase of the main Local Oscillator (LO) in a single device after each power-up or change of parameters. This means that the calibration result is not persistent and has to be performed during runtime after the parameters have been set. What is more, the accuracy of the calibration may be affected by manufacturing and component tolerance across signal paths and devices. Due to the cross-talk, an additional transmitter is required to provide a synchronizing tone distributed across all devices.

A simple, yet possibly less accurate method of front end synchronization is provided in [13]. The received signals are visually aligned in an interactive software environment by introducing an additional phase shift. It is done with the reference signal connected to all RX ports via a splitter. In addition, amplitude differences are noted. Whereas it might not be the most accurate method, it may be valid for quick alignment of phases and amplitudes of received signals.

Thermal effects associated with the heat up of SDR devices may introduce drifts or fluctuations of the phase shift coefficient. In [14], the phase drift introduced by hardware heat-up of a USRP X310 is measured over time. The calibration phase coefficient is shown to change over time. As such, delay from the last calibration routine can increase phase error that affects the estimated AoA. The work proposes an over the air calibration method using periodic, pulsed signals. A single reference antenna is placed in front of the center of the array and transmits pulses of the sine wave. Taking into account the calculated Euclidean distances from the reference antenna to RX antennas, the expected phase shift introduced by propagation is compensated while calculating the calibration phase coefficients among RX antennas.

In this work, an AoA implementation using a cheap SDR device, namely USRP B210, is presented. The main focus is on factors limiting the accuracy of such a setup. An analytical model of time, frequency, and phase error are presented. While the time alignment is obtained via software procedures embedded in the SDR’s driver and frequency synchronization results from the utilization of a common LO, phase alignment has to be obtained separately. Wired calibration using a single tone is used. Calibration using the same and separate TX is compared. Measurements show, e.g., significant phase variation in frequency and the utilized radio unit. The influence of thermal effects and the utilized RX gains are measured. All these results can be useful for other researchers planning to implement AoA estimation using the B210 platform even if another synchronization method is used. Secondly, the influence of the radio environment is considered. A proper measurement procedure is suggested to combat multipath propagation effects. Moreover, a combination of filtering and averaging is shown to increase robustness against radio interference. The proposed routines for calibration and angle-of-arrival estimation using the Root-MUSIC algorithm are validated by measurements.

The main contribution of this paper is:

  • Fully documented, open-source, and tested software for AoA estimation in the GNU Radio environment. Phase synchronization of an antenna array is obtained via a wired setup within a short calibration period. The software is easily scalable for a greater number of antenna elements and is independent of the SDR device.

  • An investigation of the impact of crosstalk (with the derivation of upper bounds), channel gains, time, and center frequency on the value of the calibration phase obtained for a wired synchronization of USRP B210 front ends. Explanation based on the internal structure of the front end is given. The value of the calibration coefficient is compared for multiple USRP B210 units.

  • A proposal of solutions against noise, multipath, and RF interference effects on AoA estimates in the constructed system. Applied averaging, band-pass filtering and movement are verified and results are compared by tests in a real environment.

  • An assessment of the overall accuracy of a setup with 2 antennas using the Root-MUSIC AoA algorithm. A statistical characterization of the observed AoA errors depending on the source of distortion.

This paper is structured as follows: In Sect. 2 basics of AoA estimation are presented together with analytical models of synchronization errors. In Sect. 3 details of a wired phase synchronization routine are discussed, providing insight into different parameters affecting calibration. Finally, Sect. 4 concludes with a description of a field test setup and assessment of the accuracy of obtained AoA estimation results. The paper is concluded in Sect. 5.

2 AoA estimation in a linear phased array with synchronization imperfections

A uniform linear array consists of N antennas regularly separated by distance d as presented in Fig. 1 for \(N=5\). The reference point of the geometry of coordinates [0, 0, 0] in Cartesian coordinates, is set to be the center of the array.

Fig. 1
figure 1

Uniform linear array with an incident plane wave

Full size image

Let us consider a signal y(t) being transmitted with carrier frequency \(f_c\) and complex envelope s(t), i.e.,

$$\begin{aligned} y(t) = s\left( t\right) e^{j2\pi f_ct}. \end{aligned}$$
(1)

When distance d between array elements is much smaller than the distance from the signal source to the antenna array, the incident electromagnetic wave can be assumed to arrive at each antenna element from the same angle denoted as \(\theta\) in the form of a plane wave. We assume that the wireless channel scales down the received signal amplitude, identically for each receiving antenna, by a factor h. Signal y(t) arrives at the center of the array with delay \(\tau _0\). However, as a result of the array’s geometry, the signal arriving at the n-th antenna (\(n\in \{ 0,\ldots ,N-1\}\)) traveled the distance different by

$$\begin{aligned} \Delta x_n = \left( \frac{N - 1}{2} - n \right) d\cos {\theta }. \end{aligned}$$
(2)

This causes the received signal at the n-th antenna to equal

$$\begin{aligned} r_n(t) = h s\left( t-\tau _0-\frac{\Delta x_n}{c}\right) e^{j2\pi f_c\left( t-\tau _0-\frac{\Delta x_n}{c}\right) } \end{aligned}$$
(3)

where c denotes the speed of light.

Assuming the reception delay difference for the n-th antenna \(\frac{\Delta x_n}{c}\) is much smaller than the symbol duration of the complex envelope signal s(t), approximation \(s\left( t-\tau _0-\frac{\Delta x_n}{c}\right) \approx s\left( t-\tau _0\right)\) can be used. Therefore, assuming the same carrier signal \(e^{-j2\pi f_c t -j\Delta \varphi }\) of phase shift \(\Delta \varphi\) is used for down conversion at each front end and sampling moment \(t_0\) is identical at each front end, the received complex baseband signal at the n-th front end equals

$$\begin{aligned} {\tilde{r}}_n(t_0) = h s\left( t_0-\tau _0\right) e^{j2\pi f_c\left( -\tau _0-\frac{\Delta x_n}{c}\right) -j\Delta \varphi }. \end{aligned}$$
(4)

The common part of the signal arriving to each antenna can be denoted as

\({\tilde{s}}(t)=h s\left( t-\tau _0\right) e^{-j2\pi f_c\tau _0 -j\Delta \varphi }\). By introducing it to (4) and using (2) it is obtained:

$$\begin{aligned} {\tilde{r}}_n(t_0) = {\tilde{s}}(t_0) e^{-j2\pi \left( \frac{N - 1}{2} - n \right) \frac{d}{\lambda }\cos {\theta }}. \end{aligned}$$
(5)

This formula shows that in the case of perfect time and frequency synchronization of all front ends, the phase of received signals differs only in phase depending on the antenna index n and AoA \(\theta\). The above formula can be extended for a higher number of incoming signals (with different AoAs) and the presence of white noise.

Let us assume that the received signal is simultaneously sampled across all N antenna elements at time instance \(t_k\). The obtained data is denoted as a column vector of N samples \({\mathbf {r}}(t_k) :=\left[ r_0(t_k) \quad r_1(t_k) \quad \ldots \quad r_{N-1}(t_k) \right] ^T\). Multiple Signal Classification (MUSIC) algorithms exploit properties of array covariance matrix \(\mathbf {R_x}\), which can be estimated using different approaches influencing the accuracy of AoA algorithms [15]. One method is to estimate the matrix from an average of K data snapshots as:

$$\begin{aligned} \mathbf {C_x} = \frac{1}{K}\sum _{k=1}^{K}{\mathbf {r}}(t_k)\,{\mathbf {r}}^H(t_k). \end{aligned}$$
(6)

The calculated matrix is referenced as \(\mathbf {C_x}\) – the sample correlation matrix. The obtained matrix serves as input to the Root-MUSIC algorithm [15].

2.1 Front ends synchronization problem

Depending on the utilized architecture, the receiving front ends can exhibit various synchronization errors between each other. This section is to exemplify how time, frequency, and phase errors can influence the received signals used for AoA estimation. The synchronization of front ends can be considered in three domains:

Frequency: It can be assumed that the \(n-th\) receiving radio front end uses in its mixer frequency \(f_c+\Delta f_n\), that is shifted by \(\Delta f_n\) from \(f_c\). Most importantly, \(\Delta f_n\) can vary among front ends. This results in a modified form of (5) for a received signal with frequency offset denoted as \({\tilde{r}}^{\mathrm {F}}_n(t_0)\):

$$\begin{aligned} {\tilde{r}}^{\mathrm {F}}_n(t_0) = {\tilde{s}}(t_0) e^{-j2\pi \Delta f_n t} e^{-j2\pi \left( \frac{N - 1}{2} - n \right) \frac{d}{\lambda }\cos {\theta }}. \end{aligned}$$
(7)

It is visible that from the AoA estimation perspective, the received signal phase will change by a factor of \(2\pi \Delta f_n t\), i.e., proportionally to the time and frequency difference. This is solved typically by sharing a reference clock signal among the front ends.

Phase: Due to manufacturing inaccuracies and tolerance of components, the phase of the signal received by the \(n-th\) radio differs among front ends. The phase shift can be visible both at the received signal path or the mixing signal. Without loss of generality we can express it as a factor \(e^{-j\Delta \varphi _n}\), specific for a given receiving front end, modifying the locally generated signal used in the mixer. This results in a modified form of (5) for a received signal with phase offset denoted as \({\tilde{r}}^{\mathrm {P}}_n(t_0)\):

$$\begin{aligned} {\tilde{r}}^{\mathrm {P}}_n(t_0) = {\tilde{s}}(t_0) e^{-j\Delta \varphi _n} e^{-j2\pi \left( \frac{N - 1}{2} - n \right) \frac{d}{\lambda }\cos {\theta }}. \end{aligned}$$
(8)

The received signal varies among antennas by a phase shift \(\Delta \varphi _n\). While its value can range from 0 to \(2\pi\), it is typically fixed or slowly varying in time. Therefore, a common approach is to calibrate the array estimating \(N-1\) coefficients. One of the phase shifts, e.g., \(\Delta \varphi _{{\tilde{n}}}\) can be embedded as a common factor into \({\tilde{s}}(t_0)\), requiring to estimate phase shift difference \(e^{-j\left( \Delta \varphi _n-\Delta \varphi _{{\tilde{n}}}\right) }\) for \(n\in \{0,\ldots ,{\tilde{n}}-1,{\tilde{n}}+1,\ldots ,N-1\}\). For the \({\tilde{n}}\)-th antenna the coefficient is assumed to equal 1. Phase synchronization of the front ends is achieved typically with post processing where the signal received from each antenna is multiplied by the conjugation of the estimated coefficient.

Time: The received signals at all front ends should be sampled at the same time instance. Moreover, this alignment should not be lost during signal processing and provisioning to the high-level software in SDR. Assuming there is a sampling moment shift at the n-th front end \(\Delta t_n\) the received signal equals

$$\begin{aligned} {\tilde{r}}^{\mathrm {T}}_n(t_0)= {\tilde{s}}(t_0+\Delta t_n)e^{j2\pi f_c\Delta t_n} e^{-j2\pi \left( \frac{N - 1}{2} - n \right) \frac{d}{\lambda }\cos {\theta }}. \end{aligned}$$
(9)

If the time difference \(\Delta t_n\) is much smaller than the transmitted signal symbol interval, i.e., \({\tilde{s}}(t_0+\Delta t_n)\approx {\tilde{s}}(t_0)\), and not changing in time, the synchronization error causes only a constant phase shift \(2\pi f_c\Delta t_n\) that can be estimated and removed as part of phase synchronization. If this condition is not met, the complex signal envelope \({\tilde{s}}(t_0+\Delta t_n)\) will differ among front ends, preventing successful AoA estimation. Therefore, coarse sampling time alignment is a must. It is typically accomplished by a 1 Pulse Per Second (PPS) signal that is distributed among devices and serves as a gating pulse that resets timers. This signal is also available in most Global Positioning System (GPS) receivers. As mentioned above, fine time synchronization is obtained as part of the phase synchronization process.

Taking all synchronization errors (7–9) into consideration, the final model of the received signals can be expressed as:

$$\begin{aligned} {\tilde{r}}_n(t_0) = {\tilde{s}}(t_0+\Delta t_n)e^{-j2\pi (\Delta f_n t-f_c\Delta t_n) -j\Delta \varphi _n} e^{-j2\pi \left( \frac{N - 1}{2} - n \right) \frac{d}{\lambda }\cos {\theta }}. \end{aligned}$$
(10)

Notice that all the errors are visible as changes in the received signal phase. As AoA estimation is based on differences of received signals phases, this can cause a significant AoA error. Therefore, an important process in AoA estimation is the provisioning of the coarse synchronization among RX front ends and fine synchronization by proper phase rotation. While a fixed phase correcting coefficient is desired, it is possible that its measurement has to be repeated periodically or after receiver reconfiguration. This will be discussed for USRP B210 based on measurements in Sec. 3.

3 Calibration Phase Measurements for USRP B210

Phase calibration and measurements were performed with the USRP B210 SDR platform. In this device time and frequency synchronization of channels within a single unit is provided by a shared clock. In the case of multiple devices, the synchronization may be provided by reference clock and a pulse-per-second signal being fed to each SDR. The architecture of B210 guarantees that the phase shift between channels remains similar between runs for identical configurations. The constructed radio system is controlled via GNU Radio software where necessary functions and routines are implemented. The signal processing flowchart responsible for phase measurements can be seen in Fig. 2. The calibration was performed with a single tone, of a frequency 50 kHz higher than the carrier frequency, fed to the RX channels via a splitter and matched length cables. The test tone shift was performed in order to prevent LO leakage providing additional distortion of the observed tone. An additional attenuator of 30 dB mounted before the splitter is a safety measure to ensure that the input signal does not exceed the maximum tolerable power level of USRP B210 and prevents any damage to the RX chain. In the software domain, the signal is then band-pass filtered by a Finite Impulse Response (FIR) filter, with a pass band of 45-55 kHz and 10 kHz transition width. Next, the phase difference is calculated and averaged by a Moving Average Filter (MAV). In the end, the obtained stream is decimated and saved to a file. If not stated differently, the center frequency is set to 2.44 GHz. The phase synchronization routine was examined for two calibration source configurations. One with a signal from the TX of the receiving USRP (as shown in Fig. 3a) and the second with a signal provided by another USRP B210 (as shown in Fig. 3b). The sampling rate of both TX and RX is set to 1 MSPS.

Fig. 2
figure 2

Phase shift measurement flowchart

Full size image
Fig. 3
figure 3

Diagrams of USRP B210 wired phase calibration setups

Full size image

3.1 Comparison of wired synchronization setups

It was initially assumed that a single USRP B210 will be sufficient to create a self-contained system with two receiving elements and a calibration source utilizing one of the TX channels. However, this setup is prone to errors introduced by crosstalk between adjacent RX and TX channels. The crosstalk in USRP B210 is a result of its architecture as visible in Fig. 3a. The switches present in the signal chain have limited isolation and introduce coupling between TX and the closest RX channel of SDR. The calibration signal received by the front end with crosstalk can be expressed as: \(r^c(t) = Ae^{j2\pi \,ft}+Be^{j2\pi \,ft-j\varphi }\), where \(Ae^{j2\pi \,ft}\) is the signal received through the RX port (wanted). The second component is the leaked signal (unwanted) that is shifted in phase by \(\varphi\) in regard to the former. Without loss of generality, it is assumed that A and B are amplitudes, i.e., non-negative real numbers. After the downconversion, the carrier frequency component is removed, giving \(r_{bb}^c(t) = A+Be^{j\varphi }\). The difference in phase is maximal when \(Be^{-j\varphi }\) is perpendicular to A in the polar representation of complex numbers. As both A and B are non-negative real numbers and \(A>B\), the maximal phase shift introduced by B is when it is of purely complex value, i.e., \(-jB\) or \(+jB\). The maximal phase error can then be calculated based on the formed right-angled triangle as: \(\Delta _\psi = \arctan { \left( \frac{B}{A} \right) }\). When \(B<<A\), the value of arctangent can be approximated with the Maclaurin-Taylor series for arctangent, resulting in: \(\Delta _\psi \approx \frac{B}{A}\). As such, the worst case, crosstalk-originating phase estimation error can be approximated by a square root of the ratio of crosstalk and wanted signals powers.

To verify the extent of crosstalk impact on the accuracy of phase calibration, a series of measurements were performed. For RX gains of 40 dB and TX gain of 45 dB the crosstalk magnitude, i.e., B, was measured with all antenna ports of the same channel being terminated with a matched impedance load (see Fig. 3a). Next, the reference value of A was measured without the attenuator inserted between TX and RX2 ports. In this configuration, A is much greater than B, allowing the crosstalk component to be omitted. Finally, the standard phase calibration routine was executed for a few values of inserted attenuation in the TX path. Given that for constant gains of both TX and RX of USRP B210, the crosstalk level is also constant, increasing the value of attenuation reduced the desired signal, i.e., A, allowing us to investigate the calibration accuracy for various signal-to-crosstalk ratios. The results of the measurement are presented in Fig. 4. The value of A for attenuation greater than 0 dB is calculated using the value of the introduced attenuation.

First, the measured phase difference obtained for transmission from a separate TX is invariant from the attenuation value (a series denoted as Sep. TX), the increasing attenuation causes an increasing phase error for self-calibration configurations. Although the crosstalk power depends on the utilized TX channel, both the obtained bounds and the measured phase differ. However, in both cases, the measured points are within the derived bounds.

Fig. 4
figure 4

Accuracy of phase calibration in regard to attenuation attached to TX source

Full size image

In wired setups it is common to use attenuators as a safety measure to prevent any damage to the RX signal chain, the obtained results show it can lead to a significant phase calibration error, e.g., a 30 dB attenuator introduces a phase error of approximately 2-5\(^{\circ }\).

Due to the observed levels of crosstalk and its influence on phase calibration, consecutive measurements are performed with a separate USRP B210 operating as a reference TX as depicted in Fig. 3b.

3.2 Phase-time dependency

Here the phase correction coefficient was observed for a long period of time. The test lasted around a few hours. RX gains were 10 dB and TX gain was set to 50 dB. The additional safety attenuator value was 30 dB. Measurements were performed for previously unpowered devices to observe the extent of coefficient drift. The collected data was smoothed by a MAV filter of the length of 100k samples. The results presented in Fig. 5 show the initial drift caused by the heat up of the device and the distribution of the measured values after stabilization. It can be seen that the distribution of the phase difference is Gaussian once stabilized with a mean value of \(8.9^{\circ }\) and a standard deviation of \(0.05^{\circ }\). The initial drift during the first two hours of operation accounts for a change of the mean by approximately 0.07\(^{\circ }\), which is relatively small compared to the overall averaged value and may be considered negligible.

Fig. 5
figure 5

Change of phase shift correction coefficient value in wired setup over time

Full size image

3.3 Phase-frequency dependency

To analyze the dependence of the phase shift on carrier frequency, additional measurements were performed spanning the range from 350 MHz to 6 GHz in 50 MHz steps. It consisted of collecting the phase difference values over 10 s with MAV of 100k length for each carrier frequency. The procedure was repeated in 50 sweeps to check if there is any variance between repeated measurements for the same frequency. Figure 6 depicts the average of all 50 sweeps and 95% confidence intervals calculated over the means of 10 s measurements for a given frequency. It can be seen that the phase difference does not exhibit any monotonic dependency on the center frequency. This irregularity is probably due to discrete components used in the signal chain and their combined diverse phase characteristics at a given frequency. The confidence interval overlaps the mean, meaning that the phase-frequency response of the device is very stable over multiple sweeps. While the phase difference among channels significantly depends on the frequency and is fixed in time, one could consider storing its values and using them when needed. One might want to use the measured value for another B210 device.

Fig. 6
figure 6

Average of multiple frequency sweeps of phase shift coefficient value

Full size image

Aiming to understand how the phase-frequency characteristic varies between B210 devices, the frequency sweep was performed for 6 available devices, resulting in Fig. 7. From this plot it is visible that the phase-frequency characteristic is individual for each device. Small differences introduced in integrated circuits and utilized electronic components result in significant, from the AoA estimation point of view, differences in the signal phase rotation. There is no universal trend and it is hard to discern common features. The overall phase difference can be contained mostly within the \((-10^{\circ }, 20^{\circ })\) range. While the results of our measurements can potentially be used instead of calibration measurements for USRP B210, it can result in an AoA estimation error increased by around 10-20\(^{\circ }\) in some cases. Another interesting phenomenon are the steep changes in phase at the frequencies of 2.2 and 4 GHz. Those discontinuities originate from the switching of discrete component signal chains in USRP B210 due to wideband frequency matching [16].

Fig. 7
figure 7

Phase-frequency characteristic of multiple USRP B210 devices

Full size image

3.4 Phase-gain dependency

In order to investigate the influence of RX gain settings, the phase measurements were performed for a range of gain values. First, the gain of RX channel 0 has been fixed to 20 or 37 dB while the gain of the second channel was changed over the whole range, i.e., from 0 to 76 dB. The resultant phase difference significantly changes in the whole range from \(-180^{\circ }\) to \(180^{\circ }\), as shown in Fig. 8a. The steep phase changes have been linked to switches of gain of Integrated Circuits (ICs) of the RF chipset present in the USRP B210, e.g., Low Noise Amplifier (LNA) and mixer, as depicted in Fig. 3b. The distribution of the overall RX gain among IC can be found in [17]. The plots representing the integrated LNA (iLNA) and mixer gains were added to Fig. 8a to illustrate their correlation with the measured phase difference. On the other hand, when both RX channels have identical gains, the change of phase difference is much smaller, although still correlated with internal IC gain values, as shown in Fig. 8b. Throughout the whole sweep the value changes at most by 1.8\(^{\circ }\).

Fig. 8
figure 8

Phase dependence on the gain of RX front ends

Full size image

4 SDR-based angle of arrival estimation

The measured calibration phase shift allows for testing the angle of arrival estimation performance. The utilized two-antenna setup and the signal processing flowchart are shown in Fig. 9. The transmitter was a separate SDR utilizing a single TX antenna generating a continuous wave. The constructed radio system was controlled via the GNU Radio software environment. First, the signal was band-pass filtered. Next, given the measured calibration coefficient \(\Delta \varphi\), the received signal over the second channel was appropriately shifted in phase. The corrected signals were then correlated obtaining a correlation matrix according to (6). In these measurements, the snapshot size K was set to 1024, which corresponds to the correlation matrix averaging length. For the sample rate of 1 MSPS around 976 matrices per second are generated and a new AoA estimate is obtained approximately every 1 ms. Next, each correlation matrix is processed by the Root-MUSIC algorithm, returning a single value of the estimated AoA, which is saved to a file.

Fig. 9
figure 9

Angle of Arrival measurement system

Full size image

4.1 Results

The Angle of Arrival system performance was examined for various environmental conditions. Initially, the transmit node was placed indoors at an angle of 90\(^{\circ }\), 2 m from the array. Angle estimation was performed for 60 s, resulting in about 58k of AoA values. The RX gains were set to 60 dB and TX of the source to 50 dB. Figure 10 compares AoA error distribution under various conditions obtained after removing the mean value of AoA for each setup.

Fig. 10
figure 10

Probability distribution of AoA error in various conditions

Full size image

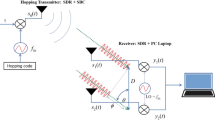
Figure 10a and b show the influence of RF interference and how AoA estimation can be improved by using band-pass filtering, respectively. The radio interference was generated by turning on a WLAN 802.11 access point nearby operating at the carrier frequency of 2.442 GHz (7th channel) and enforcing high traffic in the network. The traffic was generated by streaming a Youtube video to the smartphone to resemble a realistic scenario. The mobile device was placed approximately at the same distance to the array as the main source. The interference setup is visualized in Fig. 11.

Fig. 11
figure 11

RF interference setup

Full size image

The utilized filter had the same parameters as in the calibration tests in Sect. 3. AoA error distributions prove that band-pass filtering is absolutely necessary to limit the interference from overlapping bands in busy wireless channels. The AoA error introduced by other transmissions spreads over the whole range of estimation. The standard deviation of angle estimation without filtering equals approximately 8\(^{\circ }\). With the addition of filtering the standard deviation is decreased to only 0.3\(^{\circ }\).

Subsequent measurement was aimed at investigating how movement distorts the Angle of Arrival estimation. The RF interference was disabled in order to show a single source of distortion at a given time. The results, presented in Fig. 10c and d, were obtained with applied band-pass filtering and low RF activity in the utilized frequency band. The movement was introduced by a person walking around the system without crossing the Line-of-Sight between TX and RX antennas. The AoA estimation error introduced by movement dominates other sources and ranges between \(\pm 10^{\circ }\) with a standard deviation of 2.2\(^{\circ }\). This shows that multi-path propagation has a significant impact on AoA estimation and a proper averaging of obtained AoA values and measurement procedure design is needed to combat this error.

Therefore, measurements in an outdoor scenario were carried with both transmitter and receiver distanced from the buildings (by at least 10 m) and ground (by using 2m-high tripods). Moreover, the transmitter used a directional antenna. The applied measures were to limit the total power of non-Line-of-Sight components. RF interference was not generated as the expected conclusions are the same as in the indoor scenario. The signal source has been placed at angles 90\(^{\circ }\) and 135\(^{\circ }\) at a distance of 5 m. The setup operated at the frequency of 2.44 GHz with active band-pass filtering. The first series of measurements were performed for the source antenna in a fixed position. Then the source was moved slightly forward and backward maintaining the angle to modify potential fadings.

The obtained results are shown in Fig. 12. Here, the AoA error was calculated with respect to the known source location. First, outdoor measurements with movement show a smaller standard deviation than indoor measurements. This proves that if moving elements of the environment are more distanced, as in our outdoor setup, the signal reflected from them has a smaller influence on the total received signal. Additionally, a comparison of static and moving measurements in the outdoor scenario shows that AoA estimation can generally be improved by changes in multi-path propagation. While the static measurements exhibit a much lower variance of the result, they are biased by a significant error compared to the series with movement, i.e., the mean error is on average higher. Moving the antenna helps to visualize that the multi-path effect has a crucial impact on the performance of the AoA estimation system. It can be noted that the AoA error of static measurement constitutes a part of the distribution obtained for the measurements with movements. Therefore, it can be recommended to perform AoA estimation in the environment with movement, both indoors and outdoors, providing a sufficiently long AoA estimates averaging period. The recommended averaging duration should span the maximum time the target is at a given AoA to utilize all variations of multipath propagation.

Fig. 12
figure 12

Accuracy of the AoA system in field tests

Full size image

5 Conclusions

It is possible to build an accurate AoA estimator using a cheap SDR platform. While USRP B210 provides accurate enough time and frequency synchronization, phase synchronization has to be implemented by the user. Wired calibration is suggested. While the obtained correction coefficient is relatively stable in time, it requires recalibration after changing the front end setup, e.g., carrier frequency, or when changing the utilized device. While measuring AoA using the Root-MUSIC algorithm in a real environment it is recommended to employ filtering to remove adjacent radio interference and use AoA averaging and movement of RX or TX devices to cope with multipath propagation. This should result in a 2 antenna AoA estimation error smaller than \(10^{\circ }\) in most environments, enabling, e.g., short-range coarse positioning or algorithms enhancing network performance. However, the obtained accuracy depends on many factors including radio propagation conditions. Moreover, it can be improved by increasing the number of utilized antennas [18]. Finally, the positioning error depends on the AoA error in addition to the utilized positioning algorithm or the number of AoA-reporting nodes [19]. The implemented AoA estimation software is publicly available at [20].