Abstract
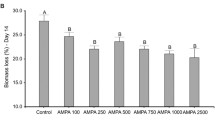
Pesticides’ sublethal effects are not regularly taken into account when assessing agrochemical’s toxicity. With the objective of detecting chronic, sublethal effects of the widely used herbicide glyphosate, an experiment was performed using the earthworm Eisenia fetida as model organism. Earthworm adults were randomly assigned to three glyphosate treatments: control (no glyphosate), regular dose for perennial weeds, and double dose. Six E. fetida individuals were placed in each pot. Two random pots were taken weekly from each treatment and the number of adults, individual weight, number of cocoons, and presence and number of young earthworms were recorded. A matrix analysis was performed with the data. The matrix population model built showed that while the control population had a positive growth rate, both glyphosate treatments showed negative growth rates. The results suggest that under these sublethal effects, non-target populations are at risk of local extinction, underscoring the importance of this type of studies in agrochemical environmental risk assessment.


Similar content being viewed by others
References
Abdullah, M., Singh, J., & Sohal, B. (2006). Behavioral hormoligosis in oviposition preference of Bemisia tabaci on cotton. Pesticide Biochemistry and Physiology, 84, 10–16.
Antón, F. A., Laborda, E., Laborda, P., & Ramos, E. (1993). Carbofuran acute toxicity to Eisenia foetida Savigny. Earthworms. Bulletin of Environmental Contamination and Toxicology, 50, 407–412.
Billoir, E., Péry, A. R. R., & Charles, S. (2007). Integrating the lethal and sublethal effects of toxic compounds into the population dynamics of Daphnia magna: a combination of the DEBtox and matrix population models. Ecological Modelling, 203, 204–214.
Casabé, N., Piola, L., Fuchs, J., Oneto, M. L., Pamparato, L., Basack, S., Giménez, R., Massaro, R., Papa, J., & Kesten, E. (2007). Ecotoxicological assessment of the effects of glyphosate and chlorpyrifos in an Argentine soya field. Journal of Soils and Sediments, 7, 232–239.
Caswell, H. (2001). Matrix population models—construction, analysis, and interpretation. Sunderland: Sinauer Associates Inc.
Charles, S., Billoir, E., Lopes, C., & Chaumot, A. (2009). Matrix population models as relevant modeling tools in ecotoxicology. Ecotoxicology Modeling 2, 261–298.
Cox, C. (1995). Glyphosate, part 2: human exposure and ecological effects. Journal of Pesticide Reform, 15, 14–20.
Edwards, C. A., & Bohlen, P. J. (1996). Biology of earthworms (3rd ed.). London: Chapman & Hall.
Emlen, J. M., & Springman, K. R. (2007). Developing methods to assess and predict the population level effects of environmental contaminants. Integrated Environmental Assessment and Management 3, 157–165.
FAO (2012). Internet resource URL: http://www.fao.org/agronoticias/agro-noticias/detalle/en/c/161730/ Last accessed: February 21, 2013.
Farji-Brenner, A. G., de Torres Curth, M. I., Casanovas, P. V., & Naim, P. N. (2003). Consecuencias demográficas del sitio de nidificación en la hormiga cortadora de hojas Acromyrmex lobicornis: un enfoque utilizando modelos matriciales. Ecología Austral, 13, 183–194.
Gimsing, A. L., Borggaard, O. K., Jacobsen, O. S., Aamand, J., & Sørensen, J. (2004). Chemical and microbiological soil characteristics controlling glyphosate mineralisation in Danish surface soils. Applied Soil Ecology, 27, 233–242.
Harper, E., Rittenhouse, T., & Semlitsch, R. (2008). Demographic consequences of terrestrial habitat loss for pool-breeding amphibians: predicting extinction risks associated with inadequate size of buffer zones. Conservation Biology, 22, 1205–1215.
ISO (International Organization for Standardization) (1993). 11268–1: Soil quality—effects of pollutants on earthworms (Eisenia fetida)—part 1: determination of acute toxicity using artificial soil substrate.
ISO. (International Organization for Standardization) (1998). 11268–2. Soil quality—effects of pollutants on earthworms (Eisenia fetida)—part 2: determination of effects on reproduction.
James, C. (2011). Global status of commercialized biotech/GM crops: 2011. ISAAA brief no. 43. Ithaca: ISAAA.
Judas, M. (1988). The species. Oecologia, 76, 579.
Lavelle, P., & Spain, A. (2001). Soil ecology. Dordrecht: Kluwer Academic Publishers.
Lavelle, P., Barois, J., Martin, A., Zaidi, Z., Schaefer, R. (1989). Management of earthworm populations in Agro-ecosystem. A possible way to maintain soil quality?. In M. Charholm & K. Bergstrom (eds.), Ecology of arable lands. Perspectives and Challenges Proceedings of an International Symposium, June 9-12, 1987, Swedish University of Agricultural Sciences, Uppsala, Sweden. Series: Developments in Plant and Soil Sciences, Vol. 39. Springer.(pp. 109–122)
Lee, K. (1985). Earthworms. Their ecology and relationships with soils and land use. North Ryde: Academic. 411 pp.
Leslie, P. H. (1945). On the use of matrices in certain population mathematics. Biometrika, 33, 184–212.
Leslie, P. H. (1948). Some further notes on the use of matrices in population mathematics. Biometrika, 35, 213–245.
Momo, F. & Falco, L. (2009). Biología y ecología del suelo.142-143. Imago Mundis (ed). Universidad Nacional de General Sarmiento, Buenos Aires, Argentina
Morse, J. G. (1998). Agricultural implications of pesticide-induced hormesis of insects and mites. Human and Experimental Toxicology, 17, 266–269.
Neuhauser, E., & Callahan, C. (1990). Growth and reproduction of the earthworm Eisenia fetida exposed to sublethal concentrations of organic chemicals. Soil Biology and Biochemistry, 22, 175–179.
OECD. Organization for Economic Co-Operation and Development, Paris, France (2004). Guideline for testing of chemicals. 222, Earthworm reproduction test (Eisenia fetida/andrei).
Pengue, W. A. (2000). Cultivos transgénicos ¿Hacia dónde vamos? Buenos Aires: Lugar Editorial.
Pérez-Jones, A., Park, K. W., Colquhoun, J., Mallory-Smith, C., & Shaner, D. (2005). Identification of glyphosate-resistant ryegrass (Lolium multiflorum) in Oregon. Weed Science, 53, 775–779.
Piccolo, A., & Celano, G. (1994). Hydrogen bonding interactions between the herbicide glyphosate and water-soluble humic substances. Environmental Toxicology and Chemistry, 13, 1737–1741.
Qaim, M. (2005). Agricultural biotechnology adoption in developing countries. American Journal of Agricultural Economics, 87, 1317–1324.
Reinecke, A. J., & Venter, J. M. (1987). Moisture preferences, growth and reproduction of the compost worm Eisenia fetida (Oligochaeta). Biology and Fertility of Soils, 3, 135–141.
Reynolds, J. W. (1996). Earthworms biology and ecology (Course manual. Pp 40–139. U.N. Córdoba, Facultad de Cs). Córdoba Argentina: Exactas.
Sprankle, P., Meggitt, W., & Penner, D. (1975). Rapid inactivation of glyphosate in the soil. Weed Science, 23, 224–228.
Spurgeon, D., Svendsen, C., Kille, P., Morgan, A., & Weeks, J. (2004). Responses of earthworms (Lumbricus rubellus) to copper and cadmium as determined by measurement of juvenile traits in a specially designed test system. Ecotoxicology and Environmental Safety, 57, 54–64.
Trigo, E., & Cap, E. (2003). The impact of the introduction of transgenic crops in Argentinean agriculture. AgBioforum, 6, 87–94.
USDA. (2010). Keys to soil taxonomy. United States Department of Agriculture. Natural Resources Conservation Center. Eleventh Edition, 338 pp.
U S Environmental Protection Agency (1999). Technical fact sheets on: glyphosate. National primary drinking water regulations.
Venkateswara Roa, J., Sutya Pavan, Y., & Madhavendra, S. (2003). Toxic effects of chlorpyrifos on morphology and acetylcholinesterase activity in the earthworm, Eisenia foetida. Ecotoxicology and Environmental Safety, 54, 296–301.
Venter, J. M., & Reinecke, A. J. (1988). The life-cycle of the compost worm Eisenia fetida (Oligochaeta). South African Journal of Zoology, 23, 161–165.
Viswanathan, R. (1992). Study of pesticides impact on earthworms using closed laboratory model ecosystem. Greig-Smith, Becker, Edwards y Heinnbach (Eds.). Ecotoxicology of earthworms.Andover, Hampshire: Intercept. pp 269
Wakelin, A. M., Lorraine-Colwill, D. F., & Preston, C. (2004). Glyphosate resistance in four different populations of Lolium rigidum is associated with reduced translocation of glyphosate to meristematic zones. Weed Research, 44, 453–459.
Welten, R. (2000). Ecotoxicity of contaminated suspended solids for filter feeders (Daphnia magna). Archives of Environmental Contamination and Toxicology, 39, 315–323.
Zang, Y., Zhong, Y., Luo, Y., & Kong, Z. (2000). Genotoxicity of two novel pesticides for the earthworm, Eisenia fetida. Environmental Pollution, 108, 271–278.
Zoran, M. J., Heppner, T. J., & Drewes, C. D. (1986). Teratogenic effect of the fungicide Benomyl on posterior segmental regeneration in the earthworms Eisenia fetida. Pesticide Science, 17, 641–652.
Author information
Authors and Affiliations
Corresponding author
Additional information
Capsule
Non-target organisms can be at risk of local extinction due to agrochemicals chronic sublethal effects, which are not consistently taken into account in toxicity and risk assessment studies.
Rights and permissions
About this article
Cite this article
Santadino, M., Coviella, C. & Momo, F. Glyphosate Sublethal Effects on the Population Dynamics of the Earthworm Eisenia fetida (Savigny, 1826). Water Air Soil Pollut 225, 2207 (2014). https://doi.org/10.1007/s11270-014-2207-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11270-014-2207-3