Skip to main content
SpringerLink
Log in

Developing the Regional Nonstationary IDF Curves Using NGN-ProNEVA Framework

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

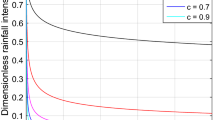
Intensity–Duration–Frequency (IDF) curves are known as practical tools in the construction of infrastructures. However, developing such curves is restricted in many regions due to sparse and insufficient record length of in-site rainfall observations. It is hence recommended to generate the regional curves. According to the hydro-climate variability and change during the recent decades, it is essential to consider the non-stationarity of hydro-climate variables. In this research, the Neural Gas network (NGN) coupled with ProNEVA have been applied to develop non-stationary regional IDFs. The l-moments approach was used to plot regional stationary IDF curves to compare the results of non-stationary IDFs for homogenous regions. The results showed that the regional nonstationary curves had overestimated rainfall intensity compared with the regional stationary curves which can attribute to the decreasing trend of rainfall over the study area. The average value of overestimation in the return period of 2 years was equal to 50 percent. This overestimation was more significant for lower return periods, which indicates that the nonstationary approach is more important for short-duration events. The return period of 100 years is equal to 25 percent in region two, and in region one, it is equal to 20 and 43 percent, respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Availability of Data and Material

Not applicable.

Code Availability

Not applicable.

References

  • Abdi A, Hassanzadeh Y, Ouarda TB (2017) Regional frequency analysis using Growing Neural Gas network. J Hydrol 550:92–102

    Article  Google Scholar 

  • Agilan V, Umamahesh NV (2016) Is the covariate based non-stationary rainfall IDF curve capable of encompassing future rainfall changes? J Hydrol 541:1441–1455

    Article  Google Scholar 

  • Aho K, Derryberry D, Peterson T (2014) Model selection for ecologists: the worldviews of AIC and BIC. Ecology 95(3):631–636

    Article  Google Scholar 

  • Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom 19(6):716–723

    Article  Google Scholar 

  • Alemaw BF, Chaoka RT (2016) Regionalization of rainfall intensity-duration-frequency (IDF) curves in Botswana. J Water Resour Prot 8(12):1128

    Article  Google Scholar 

  • Asadieh B, Krakauer NY (2015) Global trends in extreme precipitation: climate models versus observations. Hydrol Earth Syst Sci 19(2):877–891

    Article  Google Scholar 

  • Blanchet J, Ceresetti D, Molinié G, Creutin JD (2016) A regional GEV scale-invariant framework for Intensity–Duration–Frequency analysis. J Hydrol 540:82–95

    Article  Google Scholar 

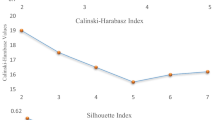
  • Caliński T, Harabasz J (1974) A dendrite method for cluster analysis. Commun Stat-Theory Methods 3(1):1–27

    Article  Google Scholar 

  • Cavanaugh NR, Gershunov A, Panorska AK, Kozubowski TJ (2015) The probability distribution of intense daily precipitation. Geophys Res Lett 42(5):1560–1567

    Article  Google Scholar 

  • Cheng L, AghaKouchak A (2014) Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci Rep 4(1):1–6

    Article  Google Scholar 

  • Chou CH, Su MC, Lai E (2004) A new cluster validity measure and its application to image compression. Pattern Anal Appl 7(2):205–220

    Article  Google Scholar 

  • Dixit S, Jayakumar KV (2022) A non-stationary and probabilistic approach for drought characterization using trivariate and pairwise copula construction (PCC) model. Water Resour Manag 36(4):1217–1236

    Article  Google Scholar 

  • Fritzke B (1995) A growing neural gas network learns topologies. Neur Inf Sys 625–632

  • Ganguli P, Coulibaly P (2017) Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol Earth Syst Sci 21(12):6461–6483

    Article  Google Scholar 

  • Gao M, Mo D, Wu X (2016) Nonstationary modeling of extreme precipitation in China. Atmos Res 182:1–9

    Article  Google Scholar 

  • Gilks WR, Richardson S, Spiegelhalter D (1995) Markov chain Monte Carlo in practice. CRC Press

    Book  Google Scholar 

  • Gohari A, Shahrood AJ, Ghadimi S, Alborz M, Patro ER, Klöve B, Haghighi AT (2022) A century of variations in extreme flow across Finnish rivers. Environ Res Lett 17(12):124027

    Article  Google Scholar 

  • Hardy JT (2003) Climate change: causes, effects, and solutions. John Wiley & Sons

    Google Scholar 

  • Hosking JR (1990) L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J R Stat Soc: Series B (methodological) 52(1):105–124

    Google Scholar 

  • Hosking JRM, Wallis JR (1993) Some statistics useful in regional frequency analysis. Water Resour Res 29(2):271–281

    Article  Google Scholar 

  • Jamali M, Gohari A, Motamedi A, Haghighi AT (2022) Spatiotemporal changes in air temperature and precipitation extremes over Iran. Water 14(21):3465

    Article  Google Scholar 

  • Kendall M (1962) Rank CorrelationMethods, 3rd edn. Hafner PublishingCompany, New York

    Google Scholar 

  • Lee SH, Maeng SJ (2003) Frequency analysis of extreme rainfall using L-moment Irrigation and Drainage. The Journal of the International Commission on Irrigation and Drainage 52(3):219–230

    Article  Google Scholar 

  • Lenderink G, Van Meijgaard E (2008) Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat Geosci 1(8):511–514

    Article  Google Scholar 

  • Li J, Lei Y, Tan S, Bell CD, Engel BA, Wang Y (2018) Nonstationary flood frequency analysis for annual flood peak and volume series in both univariate and bivariate domain. Water Resour Manage 32:4239–4252

    Article  Google Scholar 

  • Lima CH, Kwon HH, Kim JY (2016) A Bayesian beta distribution model for estimating rainfall IDF curves in a changing climate. J Hydrol 540:744–756

    Article  Google Scholar 

  • Mahmoudi MR, Eslamian S, Soltani S, Tahanian M (2023) Correction to: Regionalization of rainfall intensity–duration–frequency (IDF) curves with L-moments method using neural gas networks. Theoret Appl Climatol 51(1–2):1–11

    Article  Google Scholar 

  • Mann HB (1945) Nonparametric tests against trend Econometrica. J Econom Soc 245–259.

  • Mohan MG, AR A, Krishnan A, Rajan A (2023) Hydrologic regionalization of non-stationary intensity–duration–frequency relationships for Indian mainland. H2Open J 6(2):223–241

    Article  Google Scholar 

  • Motamedi A, Gohari A, Haghighi AT (2023) Three-decade assessment of dry and wet spells change across Iran, a fingerprint of climate change. Sci Rep 13(1):p2888

    Article  Google Scholar 

  • Overeem I, Syvitski JP (2010) Shifting discharge peaks in Arctic rivers, 1977–2007. Geogr Ann Ser A Phys Geogr 92(2):285–296

    Article  Google Scholar 

  • Perica S, Dietz S, Heim S, Hiner L, Maitaria K, Martin D, Pavlovic S, Roy I, Trypaluk C, Unruh D, Yan F (2011) Precipitation-Frequency Atlas of the United States Volume 6 Version 23, California

  • Ragno E, AghaKouchak A, Cheng L, Sadegh M (2019) A generalized framework for process-informed nonstationary extreme value analysis. Adv Water Resour 130:270–282

    Article  Google Scholar 

  • Rao AR, Hamed KH (1997) Regional frequency analysis of Wabash River flood data by L-moments. J Hydrol Eng 2(4):169–179

    Article  Google Scholar 

  • Rosner A, Vogel RM, Kirshen PH (2014) A risk-based approach to flood management decisions in a nonstationary world. Water Resour Res 50:1928–1942

    Article  Google Scholar 

  • Rousseeuw PJ (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20:53–65

    Article  Google Scholar 

  • Sarhadi A, Soulis ED (2017) Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys Res Lett 44(5):2454–2463

    Article  Google Scholar 

  • Schwarz G (1978) Estimating the dimension of a model. Ann Stat 461–464

  • Singh D, Horton DE, Tsiang M, Haugen M, Ashfaq M, Mei R, Rastogi D, Johnson NC, Charland A, Rajaratnam B, Diffenbaugh NS (2014) Severe precipitation in Northern India in June 2013: Causes, historical context, and changes in probability Bull Am. Meteorol Soc 95(9):S58–S61

    Google Scholar 

  • Smith RL (2001) Extreme value statistics in meteorology and the environment. Environ Stat 8:300–357

    Google Scholar 

  • Tramblay Y, Neppel L, Carreau J, Sanchez-Gomez E (2012) Extreme value modelling of daily areal rainfall over Mediterranean catchments in a changing climate. Hydrol Process 26(25):3934–3944

    Article  Google Scholar 

  • Tsakiris GP, Loucks DP (2023) Adaptive water resources management under climate change: An introduction. Water Resour Manag 1–13

  • Vasiliades L, Galiatsatou P, Loukas AJ (2015) Nonstationary frequency analysis of annual maximum rainfall using climate covariates. Water Resour Manag 29:339–358

    Article  Google Scholar 

  • Veneziano D, Yoon S (2013) Rainfall extremes, excesses, and intensity-duration-frequency curves: A unified asymptotic framework and new nonasymptotic results based on multifractal measures. Water Resour Res 49(7):4320–4334

    Article  Google Scholar 

  • Villarini G, Serinaldi F, Smith JA, Krajewski WF (2009) On the stationarity of annual flood peaks in the continental United States during the 20th century. Water Resour Res 45(8)

  • Westra S, Fowler HJ, Evans JP, Alexander LV, Berg P, Johnson F, Kendon EJ, Lenderink G, Roberts N (2014) Future changes to the intensity and frequency of short-duration extreme rainfall. Rev Geophys 52(3):522–555

    Article  Google Scholar 

  • Xu L, Zhou H, Du L, Yao H, Wang H (2015) Precipitation trends and variability from 1950 to 2000 in arid lands of Central Asia. J Arid Land 7(4):514–526

    Article  Google Scholar 

  • Yang L, Li J, Kang A, Li S, Feng P (2020) The effect of nonstationarity in rainfall on urban flooding based on coupling SWMM and MIKE21. Water Resour Manag 34:1535–1551

    Article  Google Scholar 

  • Yue S, Pilon P, Cavadias G (2002) Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J Hydrol 259(1–4):254–271

    Article  Google Scholar 

Download references

Acknowledgements

The authors appreciate the constructive comments of anonymous reviewers on this paper, which helped improve the final version of the paper.

Funding

This research received no external funding.

Author information

Authors and Affiliations

  1. Department of Water Science and Engineering, College of Agriculture, Isfahan University of Technology, Isfahan, 8415683111, Iran

    Mohammad Reza Mahmoudi, Moein Tahanian, Alireza Gohari & Saeid Eslamian

Authors
  1. Mohammad Reza Mahmoudi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Moein Tahanian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alireza Gohari
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Saeid Eslamian
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors collaborated in the research presented in this publication by making the following contributions: research conceptualization, Mohammad Reza Mahmoudi (M.R.M.), Moein Tahanian (M.T.), Alireza Gohari (A.G.), Saeid Eslamian (S.E.); methodology, M.R.M., A.G., and S.E.; formal analysis, M.R.M, A.G., and S.E; writing—original draft preparation, M.R.M, M.T., and A.G.; writing—review and editing, M.R.M, M.T., and A.G.; supervision, A.G. and S.E.,

Corresponding author

Correspondence to Mohammad Reza Mahmoudi.

Ethics declarations

Ethics Approval

We confirm that this article is original research and has not been published or presented previously in any journal or conference in any language.

Consent to Participate

Not applicable.

Consent for Publication

All the authors consented to publish the paper.

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahmoudi, M.R., Tahanian, M., Gohari, A. et al. Developing the Regional Nonstationary IDF Curves Using NGN-ProNEVA Framework. Water Resour Manage 37, 5581–5599 (2023). https://doi.org/10.1007/s11269-023-03619-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-023-03619-5

Keywords

Search

Navigation