Abstract
Water stress conditions associated with population growth, climate change, and groundwater contamination, represent a significant challenge for all stakeholders in the water sector. Increasing the resilience of Water Supply Systems (WSSs) becomes of fundamental importance: along with an adequate level of service, sustainability targets must be ensured. A long-term management strategy is strictly connected to a holistic approach, based on analyses at different scales. To this end, both groundwater modeling tools and water management models, with different spatial and temporal scales, are routinely and independently employed. Here, we propose a coupled approach combining: i) groundwater models (MODFLOW) to investigate different stress scenarios, involving climate change and anthropic activities; ii) water management models (Aquator), to assess the water resources availability and the best long-term management strategy for large-scale WSS. The management models are implemented starting from input and output flows derived by groundwater models: this leads to establish a comprehensive framework usually not defined in management models and including a quantitative characterization of the aquifer. The proposed methodology, general and applicable to any study area, is here implemented to the WSS of Reggio Emilia Province, and its main groundwater resource, the Enza aquifer, considering three different stress scenarios for groundwater models (BAU, ST1, and ST2), and for management strategies (BAU, BAURV2, ST2). Among the key results, we observe that coupling the two model types: i) allows evaluating water resources availability in connection with management rules; ii) leads to examining more realistic operation choices; iii) permits planning of infrastructures at basin scale.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Groundwater is the most exploited water resource worldwide for drinking water, irrigation and industrial purposes. The increase in water demand in urban areas, together with a limited availability, poses a considerable challenge for water companies (Koop and van Leeuwen 2017; van Leeuwen 2013). Together with these factors, population growth, climate change and contamination of water resources contribute to increasing water stress, both locally and globally (IPCC 2014).
Climate change effects on groundwater are a major concern, since hydrogeological processes may be directly and indirectly affected. Several studies showed that this still represents an open chapter (Mehrazar et al. 2020; Amanambu et al. 2020), suggesting the need for a deeper comprehension of the complex physical processes and interactions between climate and groundwater. Furthermore, the lack of sufficient data makes it very difficult to understand the impacts that climate change may have on groundwater resources. Freshwater resources are vulnerable and can be strongly influenced by climate change, with wide-ranging consequences for societies and ecosystems (Kundzewicz et al. 2007).
It is therefore of fundamental importance to focus on increasing the resilience of Water Supply Systems (WSSs), in terms of environmental and infrastructural compliance (Pamidimukkala et al. 2021; Li and Lence 2007). Alongside adequate service levels, sustainability objectives must be ensured (Elshall et al. 2020), with economic, social, environmental, infrastructural and governance constraints that vary over time: their assessment is critical for water companies in the long-term. Management strategies need to improve the resilience of WSS and account for the sustainability of water withdrawals (Marques et al. 2015; Hernández-Bedolla et al. 2017). Increasing the resilience of WSS, under a sustainability perspective, has been widely analyzed in several studies (Liu et al. 2012; Felisa et al. 2019; Liserra et al. 2016), aiming to identify performance indicators to assess and support decision strategies.
Proper managements of water resources must ensure that the needs of private users, agricultural production centers, and industrial activities are met, while protecting the sources of supply. The management should be carried out in optimized way, i.e. determining the solution that satisfies demand while minimizing costs, and identifying alternative strategies in case of unavailability of resources normally exploited. The optimized management should be also accompanied by a sustainability assessment aimed at preserving water resources from pollution and excessive withdrawals. Under this perspective, the combination of different models at different scales may improve the comprehension of real WSS and sources exploitation. Groundwater modelling has been widely investigated, and several studies focused on its use to support resource planning and water management (Mirdashtvan et al. 2021; Mussa et al. 2020). Groundwater models lead to understand the dynamics of groundwater systems and the processes affecting their output, especially if linked to human activities (Vadiati et al. 2018; Ali et al. 2020).
Combining optimization management strategies with groundwater dynamics allows to link two different actors, i.e. the WSS and its supply sources, usually disconnected in terms of management. In fact, optimization models typically consider the groundwater resources as infinite, given their focus on supporting management strategies under an economic and sustainability perspective: this approach represents a limitation, as it doesn’t represent the real behavior of subsurface resources.
In order to characterize the WSS with a holistic approach, in this study we adopt a novel methodology, combining groundwater flow models (developed with MODFLOW) able to describe groundwater availability and its variation over time, with optimization models (developed with Aquator), to simulate changes in surface runoff and design an additional network element, a reservoir, serving extra irrigation/industrial demand. The latter tool is widely adopted by UK water companies and employed in different studies to verify the capacity of supply networks and the exploitation of their resources (Morley and Savić 2020; Arena et al. 2015), to develop conscious and sustainable withdrawal strategies. The joint use of these models allows assessing the current state of the WSS and predict the main trend of aquifer behaviour, under different stress scenarios.
In the following, the general methodology is presented, focusing on the models adopted in this study (Sect. 2.1). The approach is applied to a specific area, described in Sect. 2.2; different stress scenarios are considered for both groundwater models (Sect. 2.3), and management models (Sect. 2.4). Results of the modeling are discussed in Sect. 3, presenting trends of key variables related to groundwater availability and the management of the added reservoir. A set of conclusions and perspectives for future work (Sect. 4) closes the paper.
2 Material and Methods
2.1 Methodology
The methodology applied in this study combines two different types of analyses: (i) groundwater models, to describe the hydrodynamic behavior of the main aquifer feeding the WSS, under different stress scenario; (ii) management optimization models, to characterize the WSS with a simplified schematization.
We start with groundwater modeling to understand the input and output variables involved in the aquifer dynamics, under three different scenarios. These analyses also allow to quantify the available volume within the aquifer and its future trend according to climate projections.
Subsequently, the flows derived by groundwater simulations are adopted to implement optimization models. A reconstruction of the simplified WSS is conducted and the time series of the input and output flows derived by groundwater models are inserted in the different components of the skeletonization. The aquifer, typically defined as having infinite capacity, is on the contrary properly characterized by means of the input and output time series for different stress scenarios.
The proposed methodology is general and applicable to any case study. Here, we adopt this approach and apply it to a specific study area, i.e. the Enza aquifer and the WSS of Reggio Emilia Province. Figure 1 shows the models and their exchange of information: in particular, the management models also involve the presence of a reservoir element, namely RV2, to evaluate different withdrawal strategies according to increasing water demand.
2.2 Characterization of the Study Area
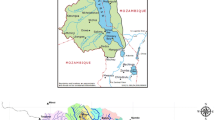
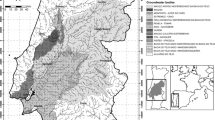
In this study we investigate the WSS of Reggio Emilia Province and its main source, i.e. the Enza alluvial fan. This aquifer represents the major groundwater reservoir of the Reggio Emilia Province, being the venue of the major well fields feeding the WSS, namely Quercioli, Roncocesi, Caprara, and S. Ilario Nuovo. Figure 2 provides a planimetric representation of the area of interest, together with the location of Enza aquifer. The main characteristics of the area, i.e. rivers, geology and hydrogeological parameters, are presented and discussed in Supplementary Materials (hereinafter SM), Text S1.1.
Water withdrawals for civil use, managed by Water Company IRETI S.p.A., take place through 59 wells active in the Reggio Emilia area, grouped into 14 well fields. In addition, 25 wells in the neighboring Parma area are considered in this study. The location of Reggio Emilia well fields and Parma wells are displayed in Fig. S3, while Fig. S4a−b show respectively the average annual volumes extracted from Parma wells, and the trend of groundwater withdrawals for civil use in the Reggio Emilia area for the 2002-2012 decade. Most of the wells interact with aquifer Group A, more exploited due to its larger permeability (Table S2). Major withdrawals are derived from Quercioli, Roncocesi, S. Ilario Nuovo and Caprara well fields, located in the northern part of the Enza alluvial fan: in the 2002-2012 period, these abstractions represent about 77% of the total withdrawals from the Enza fan. During this decade, a decrease is registered in Quercioli and Roncocesi withdrawals, while an increase is observed in S. Ilario nuovo and constant values are recorded in Caprara well fields.
Irrigation withdrawals are particularly concentrated in the plain area, where agricultural activities are intensive (Table S3): the area considered in this study is 1,137.35 km2. Industrial extractions are estimated as 19 Mm3 (Regione Emilia-Romagna 2015b), but only a small amount pertain to the Enza alluvial fan (Table S4).
A detailed discussion about natural recharge and climate change in the study area is reported in SM, Text S1.2 and S1.3 respectively.
2.3 Groundwater Models
A characterization of the hydrodynamic behavior of the aquifer can be achieved by means of groundwater flow simulations, here conducted with U.S. Geological Survey MODFLOW-NWT code (Niswonger et al. 2011).
In the following, three different cases are described: (i) the Business As Usual (BAU) case, with data from the 2002-2012 period; (ii) the Strategy 1 (ST1) case, incorporating climate change RCP4.5 scenario over a 30-year time horizon; (iii) the Strategy 2 (ST2) case, the same as ii) but assuming that a reservoir is planned for irrigation and industrial purposes in the Enza river basin.
2.3.1 Business As Usual (BAU) State
The spatial domain is discretized in a grid of 67,596 square cells (131 rows by 129 columns by 4 layers), with a dimension of 250 m. The active area of the model is about 500 km2, and is bordered by the Apennines to the south, the Parma river to the west, the Crostolo river to the east, and the A1 highway to the north. The vertical discretization is obtained considering 4 layers, all convertible, associated to the main aquifer complexes (Fig. S7b).
The horizontal hydraulic conductivity \(k_{\mathrm hor}\) of the area is deduced from the transmissivity T (Table S2): 5 areas are detected, with average values of T (Fig. S7c). For each grid cell, T is divided by the thickness of Group A, obtaining a value of \(k_{\mathrm hor}\) assumed equal for all three layers of Group A (Fig. S7d). Regarding Group B, the \(k_{\mathrm hor}\) values is obtained assuming an average transmissivity equal for the whole unit, initially corresponding to 3.93\(\times\)10-3 m2/s, and then lowered to 1.96\(\times\)10-3 m2/s after the calibration process. For both Group A and Group B, a vertical hydraulic conductivity \(k_{\mathrm vert}\) initially equal to \(k_{\mathrm hor}\)/10 is assumed.
A transient simulation is performed, considering the 2002-2012 decade and 4 stress periods (hereinafter SP) of three months for each year, coinciding roughly with the seasons: for every year, the first SP coincides with January, February, March, the second with April, May, June, the third corresponds to July, August, September, and the fourth SP coincides with October, November, December.
Specific storage (\(S_{\mathrm s}\)) and specific yield (\(S_{\mathrm y}\)) coefficients are related to the storage variation within the modeled aquifer. The value of \(S_{\mathrm s}\) is derived from the storativity S obtained from tests on some well fields, i.e. Caprara, S. Ilario Bellarosa, Roncocesi, Quercioli, Caneparini and Case Corti for aquifer Group A, and Mangalana and Aiola for Group B. Average values of S equal to 1.51\(\times\)10-4 for Group A, and to 2.02\(\times\)10-4 for Group B are obtained, corresponding to an average value of 1.76\(\times\)10-4. The spatial trend of the parameter \(S_{\mathrm s}\) is deduced for each cell, dividing the value of S by the thickness between the DEM and the base of the aquifer Group B. The parameter \(S_{\mathrm y}\) is assumed equal to 0.05 after calibration.
The initial head value for the transient simulation is obtained from a preliminary stationary simulation, considering the average forcing agents over the 2002-2012 period.
The forcing agents considered in this study are presented in Text S2.1 of SM. The calibration and validation of BAU groundwater model are discussed in SM, Text S2.2.
2.3.2 Alternative Strategies: ST1 and ST2
Strategy ST1 assumes that the RCP4.5 scenario takes place at the provincial scale (Text S1.3): the temperature and rain variations foreseen by RCP4.5 are adopted (Table S5) and used as an input to project forward to 2020-2050 the average values calculated in the 2002-2012 period. A transient simulation is performed with quarterly SP over the 30-year time horizon, for a total of 120 SPs. Natural recharge and baseflow of rivers differ with respect the BAU model, while pumping and “fontanili” (represented as drains) are supposed to be unchanged; in particular, withdrawals for civil, irrigation and industrial uses in the Reggio Emilia area are assumed to be equal to those during the last year of the transient simulation in the BAU scenario (SP37 - SP40). Considering an average runoff over the 2002-2012 period, equal to R = \(EP_{\mathrm m}\) - \(I_{\mathrm m}\) = 104.86 mm/year (Text S1.2), and the ratio \(\alpha\) between average runoff R and average effective infiltration value \(I_{\mathrm m}\) being constant (\(\alpha\) = 1.04), the climate parameters at year 2049 are estimated as follows: (i) the annual average rainfall \(P_{30}\) = \(P_{\mathrm m}\) + \(\Delta P\) = 748.23 mm/year; (ii) the annual average temperature \(T_{30}\) = \(T_{\mathrm m}\) + \(\Delta\) \(T\) = 14.60 °C; (iii) the annual average evapotranspiration \(ETR_{30}\) as 568.6 mm/year, derived by Turc equation (Text S1.2); (iv) the annual average infiltration \(I_{\mathrm {m},30}\) = (\(P_{30}\) - \(ETR_{30}\))/(1+ \(\alpha\)) = 88.26 mm/year. Here, the decrease in rainfall \(\Delta P\) is equal to 23.7 mm over the 30-year time horizon, and the increase in temperature \(\Delta\) \(T\) is 0.6°C (Table S5).
In the climate projection, the infiltration coefficients for each soil class are modified according to the average effective infiltration value \(I_{\mathrm m}\) of the 2002-2012 period: the infiltration coefficient becomes 0.48 for fine soil, 1.08 for medium texture soil, and 2.73 for coarse soil. Consequently, the recharge rates \(RR_{30}\) for the different soil types over the 30-year time horizon are obtained: 1.3\(\times\)10-9 m/s for fine-grained soils, 3\(\times\)10-9 m/s for medium-textured soils, and 7.6\(\times\)10-9 m/s for coarse-grained soils. The following quantities of interest are calculated, starting from the average values for each past SP over the 2002-2012 period: (i) the decrease in rainfall for each future SP on a quarterly scale, dividing the expected decrease equally; (ii) the annual average temperature variation; (iii) the real annual evapotranspiration (Turc equation, Text S1.2), equally distributed for all SP. The recharge rate adopted in the ST1 model for each SP (\(RR_{SP,ST1}\)) is estimated from the effective infiltration, assuming that the infiltration coefficients for each soil type remain constant throughout the simulation.
The basic runoff of the rivers also tends to decrease in strategy ST1. As a simplified assumption, the baseflows are supposed to decrease by 5% over the entire simulation horizon 2020-2050 (Table S11). Hence, the following quantities of interest are evaluated for every river: (i) the average baseflows for each season, from the BAU model; (ii) the variation coefficients for each baseflow, compared to the average baseflow in 2002 – 2012. Consequently, from the seasonal average of the variation coefficients, and assuming an annual reduction of 0.2% for baseflows, the time series of baseflows are obtained for the first (SP1 - SP40) and last (SP81 - SP120) decade of simulation (Fig. S11), multiplying the average value of the seasonal variation coefficient for each year of projection.
Strategy ST2 adopts as a reference condition the RCP4.5 scenario envisaged in ST1. From the tenth year of simulation in ST1, a variation in the Enza baseflow is assumed to take place due to the presence of the RV2 reservoir located upstream of the surface water abstraction in Cerezzola. In ST2, climate change effects are combined with natural/artificial runoff variations: here, the RV2 reservoir is designed to meet a specific additional water demand of irrigation/industrial nature, defined as surplus, evaluated as the difference between the demand calculated in Annex 2 of the Regional Law DGR 1781/2015 (Regione Emilia-Romagna 2015b), and the demand simulated in the BAU. In particular, the resulting surplus is estimated as 27.4 Mm3/year, according to data discussed in Sect. 2.2 and Text S2.1, and taken to be constant for the whole time horizon.
The RV2 reservoir is designed to ensure the respect of Enza’s Minimum Vital Flow (MVF), as downstream release: at the closure section of the Vetto basin, the MVF values are estimated as 0.77 m3/s in May - September, and 1.03 m3/s in October - April (Regione Emilia-Romagna 2015a).
A schematization of the system is represented in Fig. S12a, while Fig. S12b depicts the trend of MVF downstream from RV2 with the consequent release, considering a storage capacity of RV2 equal to 20 Mm3, with and without climate changes (i.e. ST2 and BAURV2, from Aquator models described in Sect. 2.4.2). The ST2 groundwater model is developed considering the reservoir RV2 to have a capacity able to meet the surplus of 27.4 Mm3/year. Starting from 2030 (SP37), it is further assumed that the presence of RV2 implies: i) a decrease in Enza baseflow of about 25%, compatible with its MVF; ii) a decrease in river head of about 30 cm over the entire course of the river. These reductions are verified with Aquator models (Sect. 2.4.2). All the other forcers adopted in ST1 (recharge, pumping, and drains) are assumed to be equal for ST2. The comparison between the Enza baseflow assumed in ST1 and ST2 is shown in Fig. S13.
2.4 Aquator Models
The groundwater models previously discussed allow optimizing models of the WSS by means of the Aquator software. In this study, we adopt Aquator XV OSS (2015). In general, an Aquator model is designed to meet water demand, subject to constraints, licenses and concessions, minimizing operating costs or the impact of the water resource, depending on its availability.
2.4.1 Modelling of WSS in Aquator - BAU
The BAU groundwater model (Sect. 2.3.1 and Text S2.1) allows to implement the reconstruction of the WSS in Reggio Emilia Province.
Figure 3a shows the schematization of the WSS including three basins: the Enza basin (Bacino Enza); a “dummy” basin to represent the other rivers in the study area (Altrifiumi); another “dummy” basin that represents the recharge (Recharge), derived from the BAU model. Part of the surface water flow from Enza basin is captured through a water intake (Abstraction Ab1), partly feeding the Cerezzola demand center (DC_Cerezzola). The DC_Cerezzola is also fed by the Malamassata well field (Pump_Malamassata), which draws directly from the model’s aquifer (Reservoir Enza). The outflow from Ab1 joins the flow from the Altrifiumi basin, constituting the surface runoff that potentially feeds the aquifer. Another abstraction (Abstraction Ab2) is inserted to simulate the baseflow adopted in the BAU model, which feeds directly the Enza reservoir: here, the flow time series of “Stream Leakage In” parameter (Stream In), derived from the BAU groundwater model, is assigned to the connection between Ab2 and the reservoir.
The Enza aquifer is represented by a reservoir with limited dimensions, defined through 4 parameters: (i) Initial Storage (54,373 Ml) derived as part of the available volume of the modelled area (Sect. 3.1); (ii) Capacity, taken to be double of Initial Storage (108,745 Ml); (iii) Emergency Storage, assumed equal to 10% of Capacity; (iv) Dead Storage, considered null.
The flow time series “Drains Stream Out” from the Enza reservoir, i.e. the sum of contribution derived from “Drains” and “Stream Leakage Out” of the BAU groundwater model, is assigned to the reach between the reservoir and the termination, and treated as a release from the reservoir.
Finally, the existing WSS is simplified using data provided by water company IRETI IREN (2016) (Table S12). The capacities of power plants and service reservoirs, also present in the schematization, are left undefined for the purposes of the study. Both irrigation/industrial withdrawals and the cumulative demand from Parma area are represented as two different demand centers: these simplifications are in line with the assumptions of the BAU groundwater model.
Figure S14a−d show the flow time series inserted in Aquator model. The trend of surface water flows in Bacino Enza and Altrifiumi is derived by the hydrological annals (Text S1.1) and shown in Fig. S14a: the series of inflows - outflows with missing data for the 2002-2012 period are reconstructed using a linear autoregressive model.
2.4.2 Increase in Irrigation/Industrial Demand - BAURV2, ST2
An additional reservoir RV2 (Sect. 2.3.2) is introduced upstream of Ab1 as depicted in Fig. 3b. The insertion of this element modifies the trend of water surface flows coming from the Enza basin, upstream of the abstraction Ab1. The RV2 reservoir is designed to satisfy the additional irrigation/industrial demand, taken to be constant over the simulation time horizon.
The release of a minimum flow equal to the Enza’s MVF is imposed downstream of RV2 in the river branch connected to Ab1. In this strategy, namely BAURV2, the same time series flow applied in BAU groundwater model are adopted; further contributions are the Enza’s MVF time series, and the additional irrigation/industrial demand time series, evaluated as described in Sect. 2.3.2. In BAURV2, the Capacity of RV2, and therefore the Initial Storage (50% of the Capacity) is considered as a design variable, while the value of Dead Storage is considered constant and equal to 1,000 Ml; the same holds for the Emergency Storage of 1,500 Ml. The Capacity is varied to evaluate how much additional demand RV2 is able to satisfy.
The presence of RV2 is also combined with climate change, according to RCP4.5 scenario, over the 30-year time horizon (2020 – 2050), as discussed in Sect. 2.3.2. In this case, again denominated ST2 in analogy with the groundwater model, the release from RV2 is the same adopted in BAURV2, so that the MVF in Enza river is ensured. The last decade of 2020 – 2050 is analyzed (SP81-SP120). The time series of surface flow from Enza basin decreases by 13% with respect to the monthly average value in BAU; this decrease is akin to that deduced for net recharge due to climate change. For Altrifiumi basin, an average decrease of 5% is assumed for the outflows of Termina, Masdone, Rio Zolle, Modolena and Quaresimo rivers, while the outflows of Parma and Crostolo rivers are reduced by 13% on the basis of reconstructed inflows - outflows time series, as for the Enza basin. The recharge time series in ST2, entering the Enza reservoir, is the same adopted in the ST1 groundwater flow model. The other two time series introduced in ST2, i.e. Stream Leakage In and Out and Drains, exhibit some differences, in particular during the spring. Demand centers time series, both civil and irrigation/industrial, are the same adopted in BAURV2, since it is assumed that no increase in pumping, and therefore in demand, occurs. In ST2, the Enza reservoir Capacity is increased to 217,490 Ml, with Initial Storage equal to 50% (108,745 Ml), and Emergency Storage equal to 10% (21,749 Ml); Dead Storage is assumed to be null. As in BAURV2, the Capacity of RV2 is a design variable, and thus so is the Initial Storage; again, Emergency Storage and Dead Storage are assumed to be constant and equal to 1,500 Ml and 1,000 Ml, respectively. Figure S16a shows the time series of water surface flows of Enza and Altrifiumi basins, in comparison with the 2002-2012 series, while Fig. S16b depicts the flow time series derived by groundwater model ST2 (Sect. 2.3.2) and adopted in the Aquator model.
3 Results
3.1 Groundwater Availability
The groundwater flow models presented in Sect. 2.3 allow deriving the aquifer availability in the study area.
Figure 4a shows the volumetric budget of the aquifer for the BAU scenario during the last year of simulation (2011); Fig. S17a−d show the hydraulic head within the shallowest aquifer portion. The head tends to decrease in spring and summer: in this period pumping increases, while recharge and influx from rivers tend to decrease.
The trend of the variables in the BAU model is shown in Fig. S18a−e, computed from the volumetric budget: recharge shows maximum values mainly in spring and autumn; stream leakage In, i.e. the influx of rivers into groundwater, is greater in winter and autumn; the effect of drains is minimal in spring and summer. Consequently, the trend of storage variation (storage Out – storage In) of the aquifer can be inferred from the combination of all the forcing agents: the variation is lower, and most often negative, in spring and summer, and higher, and typically positive, in autumn and winter, when the combined effect of recharge and influx from rivers is more consistent.
Considering the ST1 strategy, the results show a tendency to lower values of hydraulic head within the aquifer. The average reduction over the entire area in the last simulation year is about 1 m compared to BAU: most pronounced decreases are observed in the north and northeast areas, where the hydraulic head lowers by 3 to 4 m. The results of ST1 flow model in the last year of simulation (2049) are depicted in Fig. S19a−d.
For the same year, the volumetric budget of ST1 is reported in Fig. 4b: a positive and very marked increase in storage variation is detected in autumn, while lower values occur in spring and summer. A decrease in recharge and river inflow is observed in summer. Figure S20a−e depict the time series of the volumetric budget over the last decade of ST1: recharge and stream leakage In and Out show a slight decrease over the last decade of simulation, in line with results discussed in Text S1.3. Drains show a very significant reduction respect BAU, in particular in winter, spring and summer. Storage Out prevails over storage In (Fig. S20e): the groundwater availability decreases.
Finally, the results of ST2 strategy for the last year of simulation show a seasonal variation of hydraulic head similar to the previous cases (Fig. S21a−d): the head decreases until summer, and then increases in autumn. Comparing the respective SPs of ST1 and ST2, a greater decrease of the hydraulic head is observed in ST2, on average about 2.5 m: differences are more pronounced in the north and northeast areas, while minor variations are found in the southern zone.
Figure 4c shows the volumetric budget for ST2 in the last simulation year. As in ST1, there is a very marked increase in storage variation in autumn, while recharge shows higher values in spring and autumn. During spring, lower values are observed for influx from the river to the aquifer. Drains have no flow in spring and summer. Little variations of pumping are observed between ST1 and ST2, since the solver decreases the flow withdrawn during the simulation below a defined head variation.
The flow series derived by volumetric budget in ST2 for the last decade are depicted in Fig. S22a–e: recharge is equal to ST1, and a significant decrease is observed for stream leakage In and Out time series, due to the RV2 reservoir, whose presence interacts with surface water flow in Enza river, and consequently with inflow from the river to the aquifer. The reduction of flow from drains is also marked. The storage variation (Fig. S22e) is positive only during autumn SPs, indicating a further decrease of groundwater availability.
Considering the input and output variables derived for BAU, ST1 and ST2, averaged over the last decade of simulation, it is possible to observe that input and output totals do not change from BAU to ST1 (92 Mm3/year), while ST2 shows a decrease of 2% (90 Mm3/year). A drop of about 12% from BAU (43 Mm3/year) to ST1 (38 Mm3/year) is observed for recharge, while ST2 is equal to ST1. A slight decrease respect BAU (64 Mm3/year) occurs in withdrawals: 3% for ST1 (62 Mm3/year) and about 5% for ST2 (61 Mm3/year). The inflow from river to groundwater decreases by 11% from BAU (35 Mm3/year) to ST2 (31 Mm3/year), due to the presence of RV2. Drains show a very marked decrease, 67%, from BAU (3 Mm3/year) to ST2 (1 Mm3/year). A large variation occurs for storage In and Out compared with BAU (14 Mm3/year): storage In increases of 35% in ST1 (19 Mm3/year) and 50% in ST2 (21 Mm3/year), while storage Out increases of 21% for both ST1 and ST2 (17 Mm3/year). This leads to the conclusion that in ST1 and ST2 the reservoir function of the aquifer becomes predominant. Moreover, the increase of storage variation represents a situation where the equilibrium is not reached (storage In and Out are different): in fact, this scenario implies a constant and continuous decrease over time in natural recharge and baseflow.
An evaluation of the total available groundwater volume is possible observing the results derived by BAU, ST1 and ST2 flow models. Assuming an effective porosity of 0.1, the BAU scenario allows estimating the volume of the modelled area as approximately 4,946 Mm3. Observing the last year of simulation of ST1, and evaluating the average hydraulic head of the area, a volume of about 4,899 Mm3 is estimated. Therefore, the climate change conditions implied in RCP4.5 scenario bring a reduction in the available aquifer volume of about 47 Mm3 over a 30-year time horizon, i.e. little less than 1.6 Mm3/year on average. The decrease in aquifer capacity for ST2 is estimated in an identical fashion: the average volume during the last simulation year of ST2 is equal to 4,790 Mm3, corresponding to a decrease of about 156 Mm3 over the 30-year time horizon, in the order of 5 Mm3/year on average.
3.2 Optimal Management of RV2
The RV2 reservoir placed in Aquator models BAURV2 and ST2 (Sect. 2.4.2) modifies the water surface flow in Enza river, ensuring downstream a runoff at least equal to Enza’s MVF. For both strategies BAURV2 and ST2, a daily time step simulation is carried out over ten years, i.e. 2002-2012 (BAURV2) and 2040-2050 (ST2).
As discussed in Sect. 2.3.2, the base surplus covering the entire demand is equal to 16.9 Mm3/year for irrigation, and 10.5 Mm3/year for industrial withdrawals, for a total of 27.4 Mm3/year. A sensitivity analysis is then carried out by increasing the surplus by a fixed percentage (25% to 100%) to define the RV2 volume able to satisfy it; this analysis is performed by estimating the number of days when the demand is not met, and the value of the unmet demand (deficit). In doing so, the irrigation component of the surplus is applied only in spring and summer, while the industrial one is distributed uniformly throughout the year. In both scenarios BAURV2 and ST2, the surplus demand is the same.
The base surplus of irrigation/industrial demand can be satisfied with a relatively small reservoir volume of the order of 20 Mm3 in scenario BAURV2, while a reservoir volume of 25 Mm3 is required in scenario ST2. Clearly, larger reservoir volumes are required for increasing surplus; for both scenarios, a RV2 volume of 45 Mm3 can meet a doubling of surplus. A detailed representation is depicted in Table S13.
The number of days of failure are estimated as a function of the RV2 volume, for both BAURV2 and ST2 scenarios: as the volume increases, the days of water crisis decline; for a given RV2 volume, the number of failure days increase in ST2 due to the decrease in outflows from Enza basin. A graphical representation is provided in Fig. 5a−d. The exact value of RV2 volume able to meet a given surplus is shown in Fig. S23, for both strategies.
The trend of releases downstream in the Enza river is then investigated considering the surplus range covered by Table S13 and the RV2 volumes able to satisfy the demand. As the surplus varies (base case, +25%, +50%, +100%), different RV2 volumes are considered: 20, 25, 30, and 45 Mm3 for scenario BAURV2, and 25, 30, 35, and 45 Mm3 for ST2. The corresponding release values downstream of the RV2 reservoir are depicted in Fig. S24a–b. Increasing the surplus, the downstream release tends to decrease, reaching the MVF value that must be ensured: the number of days in a decade when the MVF is released tends to increase as a result of higher surplus (Table S14). Moreover, the variation in baseflow of the main river (ST2) associated with the presence of RV2 produces a benefit with respect to the present situation (BAU), notwithstanding the negative effects of climate change.
The variations of storage within the Enza aquifer are also analyzed according to ST2 flow model; in particular, the results derived from Aquator are compared with MODFLOW, to verify that the storage variations coincide. The inclusion of RV2 does not alter the inputs to Enza reservoir, as these flows are derived from the ST2 groundwater model, that already considers the variations, albeit hypothetical, due to climate change. Therefore, the inputs to Enza reservoir are exactly the inputs of stream In and recharge as described in Sect. 2.4.2. Figure S25 depicts the Enza storage variation derived from MODFLOW and Aquator for the ST2 scenario; results are practically identical.
In conclusion, simulations with Aquator show that RV2 does not modify the overall dynamics of the aquifer: its sizing suggests that a capacity around 25 Mm3 is already able to cover the surplus associated with the base additional water demand under climate change. This type of analysis also allows decision-makers to start from the demand to be satisfied and dimension the reservoir so that there is no deficit at all.
4 Conclusions
The coupling of two types of modeling, a groundwater simulator (MODFLOW) and an optimization tool (Aquator), enables to better characterize the interplay between management and modeling issues. The transfer of information between the modelling and management tools is a crucial issue: the latter tools often do not quantify the groundwater resource, which is considered to be unlimited, leading possibly, in turn, to unrealistic results.
In this study, the Enza aquifer is considered as a reservoir of finite capacity, with characteristics derived directly from subsurface flow modelling: this allows to examine realistic management choices. In particular, we observe that the decrease in available aquifer volume due to climate change is comparable to the capacity of RV2 reservoir (10 - 50 Mm3): this leads to consider the option of operating with managed aquifer recharge (MAR) technologies as an alternative to the reservoir to increase the available volume in the aquifer.
The present study is based on simplified assumptions, and their removal can lead in the future to an improvement of the existing models and a refinement of results. The main perspectives for future work are: i) a better description of the stress conditions of the flow models; ii) a deeper analysis of the system forcings in the climate projection; iii) a detailed implementation of actual management rules of the WSS within the model, aiming at a combined management of groundwater resources and water supply systems at basin scale; this, in turn, will allow decision-makers to better define optimal withdrawals.
The results obtained show how an integrated approach not only improves the overall decision-making and planning process, but also yields a methodology applicable to any site.
Data Availability
MODFLOW and Aquator are commercial codes.
References
Ali SR, Khan JN, Pandey Y, Dar MUD, Shafi M, Hassan I (2020) Modeling the impacts of climate change on groundwater resources: a review. Int J Environ Climate Change 10:61–76
Amanambu AC, Obarein OA, Mossa J, Li L, Ayeni SS, Balogun O, Oyebamiji A, Ochege FU (2020) Groundwater system and climate change: Present status and future considerations. J Hydrol 589:125163
Arena C, Cannarozzo M, Fortunato A, Scolaro I, Mazzola MR (2015) Sensitivity of regional water supply systems models to the level of skeletonization - a case study from Apulia, Italy. Procedia Eng 119:535–544
Elshall AS, Arik AD, El-Kadi Aly I, Pierce S, Ye M, Burnett KM, Wada CA, Bremer LL, Chun G (2020) Groundwater sustainability: a review of the interactions between science and policy. Environ Res Lett 15:093004
Felisa G, Lauriola I, Pedrazzoli P, Di Federico V, Ciriello V (2019) Sustainability analysis of alternative long-term management strategies for water supply systems: a case study in Reggio Emilia (Italy). Water 11(3):450
Hernández-Bedolla J, Solera A, Paredes-Arquiola J, Pedro-Monzonís M, Andreu J, Sánchez-Quispe ST (2017) The assessment of sustainability indexes and climate change impacts on integrated water resource management. Water 9(3):213
IPCC (2014) Climate change 2014: Impacts, adaptation, and vulnerability. Part B: Regional aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press
IREN (2016) Acquedotti: dati tecnici e risultanze analitiche all’anno 2016. Tech. rep., IREN Acqua Gas
Koop SHA, van Leeuwen CJ (2017) The challenges of water, waste and climate change in cities. Environ Dev Sustain 19:385–418
Kundzewicz ZW, Mata LJ, Arnell NW, Doll P, Kabat P, Jimenez B, Miller KA, Oki T, Sen Z, Shiklomanov IA (2007) Freshwater resources and their management. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Cambridge University Press pp. 173–210
Li Y, Lence BJ (2007) Estimating resilience for water resources systems. Water Resour Res 43(7):W07422
Liserra T, Behzadian K, Ugarelli R, Bertozzi R, Di Federico V, Kapelan Z (2016) Metabolism-based modelling for performance assessment of a water supply system: A case study of Reggio Emilia, Italy. Water Sci Technol Water Supply 16(5):1221–1230
Liu D, Chen X, Nakato T (2012) Resilience assessment of water resources system. Water Resour Manag 26:3743–3755
Marques R, Cruz N, Pires J (2015) Measuring the sustainability of urban water services. Environ Sci Pol 54:142–151
Mehrazar A, Massah Bavani AR, Gohari A, Mashal M, Rahimikhoob H (2020) Adaptation of water resources system to water scarcity and climate change in the suburb area of megacities. Water Resour Manag 34:3855–3877
Mirdashtvan M, Najafinejad A, Malekian A, Sa’doddin A (2021) Sustainable water supply and demand management in semi-arid regions: optimizing water resources allocation based on RCPs scenarios. Water Resour Manag 35:5307–5324
Morley M, Savić D (2020) Water resource systems analysis for water scarcity management: the thames water case study. Water 12(6):1761
Mussa KR, Mjemah IC, Muzuka ANN (2020) A review on the state of knowledge, conceptual and theoretical contentions of major theories and principles governing groundwater flow modeling. Appl Water Sci 10:149
Niswonger RG, Panday S, Ibaraki M (2011) MODFLOW-NWT, a Newton formulation for MODFLOW-2005. US Geological Survey Techniques and Methods 6(A37):44
Oxford Scientific Software Ltd. (2015) Aquator XV – User’s Guide
Pamidimukkala A, Kermanshachi S, Adepu N, Safapour E (2021) Resilience in water infrastructures: a review of challenges and adoption strategies. Sustainability 13:12986
Regione Emilia-Romagna (2015a) Allegato D – Individuazione del deflusso minimo vitale di riferimento. In DGR 2067/2015 – Attuazione della Direttiva 2000/60/CE: contributo della Regione Emilia-Romagna ai fini dell’aggiornamento/riesame dei Piani di Gestione Distrettuali
Regione Emilia-Romagna (2015b) DGR 1781/2015-Aggiornamento del quadro conoscitivo di riferimento (carichi inquinanti, bilanci idrici e stato delle acque) ai fini del riesame dei Piani di Gestione Distrettuali 2015-2021–Italiano
Vadiati M, Adamowski J, Beynaghi A (2018) A brief overview of trends in groundwater research: Progress towards sustainability? J Environ Manag 223:849–851
van Leeuwen CJ (2013) City blueprints: baseline assessments of sustainable water management in 11 cities of the future. Water Resour Manag 27:5191–5206
Funding
This study was performed under the Grant “Valutazione della sostenibilità dei prelievi idrici che alimentano gli acquedotti della Provincia di Reggio Emilia” (Sustainability evaluation of groundwater supply in Reggio Emilia Province) between IRETI S.p.A. and the Department of Civil, Chemical, Environmental and Materials Engineering (DICAM) of Bologna University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Felisa, G., Panini, G., Pedrazzoli, P. et al. Combined Management of Groundwater Resources and Water Supply Systems at Basin Scale Under Climate Change. Water Resour Manage 36, 915–930 (2022). https://doi.org/10.1007/s11269-022-03059-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-022-03059-7