Skip to main content
SpringerLink
Log in

Response Matrix Minimization Used in Groundwater Management with Mathematical Programming: A Case Study in a Transboundary Aquifer in Northern Greece

  • Published:
Water Resources Management Aims and scope Submit manuscript

Abstract

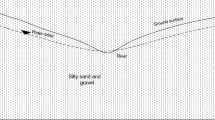
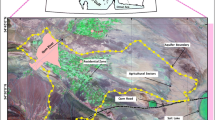
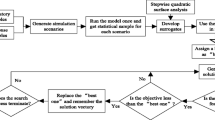
Groundwater has always been considered to be a readily available source of water for domestic, agricultural and industrial use. The last decades, the lack of policymaking for the utilization of groundwater, has led to overexploitation in many areas. The cooperation of a wide range of scientists such as mathematicians, engineers, computer scientists, environmentalists and economists – operation researchers, have led to the design and construction of commercial computer programs concerned on water management and specifically on the optimal distribution of limited water resources using groundwater management models. These combined models, via simulation and optimization algorithms, result in one optimal solution through operations research and mathematical programming methods. The groundwater management models are based on the method of space superposition or the combination of space and time superposition for steady and unsteady state problems, respectively. In the present study, an algorithm is presented, which minimizes the dimension of the response matrix, concerning on two assumptions: the first is the added fixed cost which represents the water supply pumping well and the second is the removal of time superposition. The study area is a transboundary phreatic aquifer in Northern Greece, in the area of Eidomeni, a small Hellenic village just on the borderline with FYROM. The aquifer has a total area of 10,84 km2, 26 operating – pumping wells, which the 9 of them consist control points of the hydraulic head. The number of the management periods is 12 months.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Ahlfeld, D. P., 2004, ‘Nonlinear response of streamflow to groundwater pumping for a hydrologic streamflow model,’ Adv. Water Resour, 27, 346–360.

    Article  Google Scholar 

  • Ahlfeld, D. P. and Sprong, M. P., 1998, ‘Presence of nonconvexity in groundwater concentration response functions,’ J. Water Res. PL – ASCE, 124(1), 8–14.

    Google Scholar 

  • Biswas, A. K., 1997, Water Resources. Environmental Planning, Management and Development, McGraw-Hill, New York, p. 737.

    Google Scholar 

  • Hsiao, C. T. and Chang, L. C., 2002, ‘Dynamic optimal groundwater management with inclusion of fixed costs,’ J. Water Res. PL – ASCE, 128(1), 57–65.

    Google Scholar 

  • Gorelick, S. M., 1983, ‘A review of distributed parameter groundwater management modelling methods,’ Water Resour. Res. 19(1), 305–319.

    Google Scholar 

  • Gorelick, S. M., 1990, ‘Large-scale non-linear deterministic and stochastic optimization: Formulations involving simulation of subsurface contamination,’ Math Program, 48, 19–39.

    Article  Google Scholar 

  • Greenwald, R. M., 1994, ‘MODflow MANagement: An optimization module for modflow,’ IGWMC–FOS 76 PC, Version 3.02.

  • Maddock, T., 1974, ‘Non-linear technological functions for aquifers whose transmissivities vary with drawdown,’ Water Resour. Res. 10(3), 877–881.

    Google Scholar 

  • Mc Donald, M. G., and Harbaugh, A. W., 1988, ‘A modular three-dimensional finite-difference ground-water flow model. U.S. Geological Survey Techniques of Water Resources Investigations,’ Book 6, Chap. A1, p. 586.

  • Psilovikos, A., 1999a, ‘Optimization models in groundwater management, based on linear and mixed integer programming. An application to a Greek Hydrogeological basin,’ Phys. Chem. Earth Pt B, 24(1–2), 139–144.

  • Psilovikos, A., 1999b, ‘Optimum management in groundwater resources. Comparison and evaluation with Linear and Non-Linear Programming models,’ PhD Thesis, Department of Rural and Surveying engineering, Aristotle University of Thessaloniki, Greece.

  • Psilovikos, A. and Tzimopoulos, C., 2003, ‘Time superposition removal from unit response matrix used in groundwater management,’ Hydrotechnica. 13, 87–104.

    Google Scholar 

  • Psilovikos, A., and Tzimopoulos, C., 2004, ‘Comparison of quadratic and non-linear programming (QP and NLP) optimization models in groundwater management,’ J. Hydroinform 6(2), 175–186.

    Google Scholar 

  • Spiliotopoulos, A. A., Karatzas, G. P., and Pinder, G. F., 2004, ‘A multiperiod approach to the solution of groundwater management problems using an outer approximation method,’ Eur. J. Oper. Res., 157(1), 514–525.

    Google Scholar 

  • Theodossiou, N., 2004, ‘Application of non-linear simulation and optimisation models in groundwater aquifer management,’ Wat. Resour. Manag. 18, 125–141.

    Google Scholar 

  • Tsakiris, G., 1995, Water Resources: I. Technical Hydrology, Symmetria, Athens, p. 675 (In Greek).

Download references

Author information

Authors and Affiliations

  1. Department of Agriculture Animal Production and Aquatic Environment, School of Agricultural Sciences, University of Thessaly, N. Ionia Magnisias, 38446

    Aris Psilovikos

Authors
  1. Aris Psilovikos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aris Psilovikos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Psilovikos, A. Response Matrix Minimization Used in Groundwater Management with Mathematical Programming: A Case Study in a Transboundary Aquifer in Northern Greece. Water Resour Manage 20, 277–290 (2006). https://doi.org/10.1007/s11269-006-0324-5

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11269-006-0324-5

Key Words

Search

Navigation