Skip to main content
SpringerLink
Log in

A Gromov-Hausdorff Framework with Diffusion Geometry for Topologically-Robust Non-rigid Shape Matching

  • Published:
International Journal of Computer Vision Aims and scope Submit manuscript

Abstract

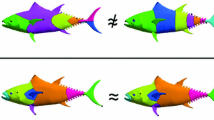
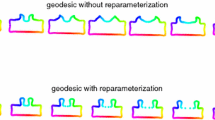
In this paper, the problem of non-rigid shape recognition is studied from the perspective of metric geometry. In particular, we explore the applicability of diffusion distances within the Gromov-Hausdorff framework. While the traditionally used geodesic distance exploits the shortest path between points on the surface, the diffusion distance averages all paths connecting the points. The diffusion distance constitutes an intrinsic metric which is robust, in particular, to topological changes. Such changes in the form of shortcuts, holes, and missing data may be a result of natural non-rigid deformations as well as acquisition and representation noise due to inaccurate surface construction. The presentation of the proposed framework is complemented with examples demonstrating that in addition to the relatively low complexity involved in the computation of the diffusion distances between surface points, its recognition and matching performances favorably compare to the classical geodesic distances in the presence of topological changes between the non-rigid shapes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Belkin, M., & Niyogi, P. (2003). Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation, 13, 1373–1396.

    Article  Google Scholar 

  • Belkin, M., Sun, J., & Wang, Y. (2009). Constructing Laplace operator from point clouds in R d. In Proc. SIAM symp. discrete algorithms (pp. 1031–1040).

  • Besl, P. J. & McKay, N. D. (1992). A method for registration of 3D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 14, 239–256.

    Article  Google Scholar 

  • Bobenko, A. I., & Springborn, B. A. (2007). A discrete Laplace–Beltrami operator for simplicial surfaces. Discrete and Computational Geometry, 38(4), 740–756.

    Article  MATH  MathSciNet  Google Scholar 

  • Boutin, M., & Kemper, G. (2004). On reconstructing n-point configurations from the distribution of distances or areas. Advances in Applied Mathematics, 32(4), 709–735.

    Article  MATH  MathSciNet  Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2005). Three-dimensional face recognition. International Journal of Computer Vision (IJCV), 64(1), 5–30.

    Article  Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2006a). Efficient computation of isometry-invariant distances between surfaces. SIAM Journal on Scientific Computing, 28(5), 1812–1836.

    Article  MATH  MathSciNet  Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2006b). Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proceedings of the National Academy of Science (PNAS), 103(5), 1168–1172.

    Article  MATH  MathSciNet  Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2007a). Calculus of non-rigid surfaces for geometry and texture manipulation. IEEE Transactions on Visualization and Computer Graphics, 13(5), 902–913.

    Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2007b). Expression-invariant representation of faces. IEEE Transactions on Image Processing, 16(1), 188–197.

    Article  MathSciNet  Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2007c). Rock, paper, and scissors: extrinsic vs. intrinsic similarity of non-rigid shapes. In Proc. int. conf. computer vision (ICCV).

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2008). Numerical geometry of nonrigid shapes. Berlin: Springer.

    Google Scholar 

  • Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2009). Topology-invariant similarity of nonrigid shapes. International Journal of Computer Vision (IJCV), 81(3), 281–301.

    Article  Google Scholar 

  • Bronstein, M. M., & Bronstein, A. M. (2009). On a relation between shape recognition algorithms based on distributions of distances (Technical Report CIS-2009-14). Technion.

  • Burago, D., Burago, Y., & Ivanov, S. (2001). A course in metric geometry. Graduate studies in mathematics, Vol. 33. Providence: AMS.

    MATH  Google Scholar 

  • Chen, Y., & Medioni, G. (1991). Object modeling by registration of multiple range images. In Proc. conf. robotics and automation.

  • Chung, F. R. K. (1997). Spectral graph theory. Providence: AMS.

    MATH  Google Scholar 

  • Coifman, R. R., & Lafon, S. (2006). Diffusion maps. Applied and Computational Harmonic Analysis, 21, 5–30.

    Article  MATH  MathSciNet  Google Scholar 

  • Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M., Nadler, B., Warner, F., & Zucker, S. W. (2005). Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proceedings of the National Academy of Sciences (PNAS), 102(21), 7426–7431.

    Article  Google Scholar 

  • Cox, T. F., & Cox, M. A. A. (1994). Multidimensional scaling. London: Chapman and Hall.

    MATH  Google Scholar 

  • DoCarmo, M. P. (1992). Riemannian geometry. Boston: Birkhäuser.

    Google Scholar 

  • Elad, A., & Kimmel, R. (2002). Spherical flattening of the cortex surface. In Geometric methods in bio-medical image processing (Vol. 2191, pp. 77–89). Berlin: Springer.

    Google Scholar 

  • Elad, A., & Kimmel, R. (2003). On bending invariant signatures for surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 25(10), 1285–1295.

    Article  Google Scholar 

  • Farin, D., de With, P. H. N., Effelsberg, W., & De, P. H. N. (2003). Recognition of user-defined video object models using weighted graph homomorphism. In SPIE IVCP.

  • Floater, M. S., & Hormann, K. (2005). Surface parameterization: a tutorial and survey. Advances in Multiresolution for Geometric modelling 1.

  • Gal, R., Shamir, A., & Cohen-Or, D. (2007). Pose-oblivious shape signature. IEEE Transactions on Visualization and Computer Graphics, 13(2), 261–271.

    Article  Google Scholar 

  • Gromov, M. (1981). Structures métriques pour les variétés riemanniennes. Textes mathématiques, no. 1.

  • Grossman, R., Kiryati, N., & Kimmel, R. (2002). Computational surface flattening: a voxel-based approach. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 24(4), 433–441.

    Article  Google Scholar 

  • Hamza, A. B., & Krim, H. (2005) Probabilistic shape descriptor for triangulated surfaces. In Proc. ICIP (pp. 1041–1044).

  • Hein, M., Audibert, J.-Y., & von Luxburg, U. (2007). Graph Laplacians and their convergence on random neighborhood graphs. Journal of Machine Learning Research, 8, 1325–1368.

    Google Scholar 

  • Hochbaum, D. S., & Shmoys, D. B. (1985). A best possible heuristic for the k-center problem. Mathematics of Operations Research, 180–184.

  • Jain, V., & Zhang, H. (2007). A spectral approach to shape-based retrieval of articulated 3D models. Computer-Aided Design, 39, 398–407.

    Article  Google Scholar 

  • Jones, P. W., Maggioni, M., & Schul, R. (2008). Manifold parametrizations by eigenfunctions of the Laplacian and heat kernels. Proceedings of the National Academy of Sciences, 105(6), 1803.

    Article  MathSciNet  Google Scholar 

  • Katz, S., Leifman, G., & Tal, A. (2005). Mesh segmentation using feature point and core extraction. The Visual Computer, 21(8), 649–658.

    Article  Google Scholar 

  • Kimmel, R., & Sethian, J. A. (1998). Computing geodesic paths on manifolds. Proceedings of the National Academy of Sciences (PNAS), 95(15), 8431–8435.

    Article  MATH  MathSciNet  Google Scholar 

  • Lafon, S. (2004). Diffusion maps and geometric harmonics. Ph.D. dissertation, Yale University.

  • Lévy, B. (2006). Laplace-Beltrami eigenfunctions towards an algorithm that “understands” geometry. In Int’l conf. shape modeling and applications.

  • Ling, H., & Jacobs, D. (2005a). Deformation invariant image matching. In Proc. ICCV.

  • Ling, H., & Jacobs, D. (2005b). Using the inner-distance for classification of articulated shapes. In Proc. CVPR.

  • Mahmoudi, M., & Sapiro, G. (2009). Three-dimensional point cloud recognition via distributions of geometric distances. Graphical Models, 71(1), 22–31.

    Article  Google Scholar 

  • Mateus, D., Horaud, R. P., Knossow, D., Cuzzolin, F., & Boyer, E. (2008). Articulated shape matching using Laplacian eigenfunctions and unsupervised point registration. In Proc. IEEE conference on computer vision and pattern recognition (CVPR).

  • Mémoli, F. (2007). On the use of Gromov-Hausdorff distances for shape comparison. In Point based graphics, Prague.

  • Mémoli, F. (2008). Gromov-Hausdorff distances in Euclidean spaces. In Proc. non-rigid shapes and deformable image alignment (NORDIA).

  • Mémoli, F. (2009). Spectral Gromov-Wasserstein distances for shape matching. In Proc. non-rigid shape analysis and deformable image alignment.

  • Mémoli, F., & Sapiro, G. (2001). Fast computation of weighted distance functions and geodesics on implicit hyper-surfaces. Journal of Computational Physics, 173(2), 730–764.

    Article  MATH  MathSciNet  Google Scholar 

  • Mémoli, F., & Sapiro, G. (2005a). Distance functions and geodesics on submanifolds of R d and point clouds. SIAM Journal of Applied Mathematics, 65, 1227–1260.

    Article  MATH  Google Scholar 

  • Mémoli, F., & Sapiro, G. (2005b). A theoretical and computational framework for isometry invariant recognition of point cloud data. Foundations of Computational Mathematics, 5, 313–346.

    Article  MATH  MathSciNet  Google Scholar 

  • Mémoli, F., Sapiro, G., & Thompson, P. (2006). Geometric surface and brain warping via geodesic minimizing Lipschitz extensions. In MFCA-2006 international workshop on mathematical foundations of computational anatomy, Copenhagen.

  • Meyer, M., Desbrun, M., Schroder, P., & Barr, A. H. (2003). Discrete differential-geometry operators for triangulated 2-manifolds. Visualization and Mathematics, III, 35–57.

    MathSciNet  Google Scholar 

  • Olver, P. (1999). Classical invariant theory. Cambridge: Cambridge University Press.

    Book  MATH  Google Scholar 

  • Osada, R., Funkhouser, T., Chazelle, B., & Dobkin, D. (2002). Shape distributions. ACM Transactions on Graphics (TOG), 21(4), 807–832.

    Article  Google Scholar 

  • Ovsjanikov, M., Sun, J., & Guibas, L. (2008). Global intrinsic symmetries of shapes. Computer Graphics Forum, 27, 1341–1348.

    Article  Google Scholar 

  • Ovsjanikov, M., Bronstein, A. M., Bronstein, M. M., & Guibas, L. (2009). Shape Google: a computer vision approach for invariant retrieval of non-rigid shapes. In Proc. non-rigid shape analysis and deformable image alignment.

  • Qiu, H., & Hancock, E. R. (2007). Clustering and embedding using commute times. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(11), 1873–1890.

    Article  Google Scholar 

  • Raviv, D., Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2007). Symmetries of non-rigid shapes. In Proc. workshop on non-rigid registration and tracking through learning (NRTL).

  • Reuter, M., Wolter, F.-E., & Peinecke, N. (2006). Laplace-Beltrami spectra as “shape-DNA” of surfaces and solids. Computer Aided Design, 38, 342–366.

    Article  Google Scholar 

  • Reuter, M., Biasotti, S., Giorgi, D., Patanè, G., & Spagnuolo, M. (2009). Discrete Laplace-Beltrami operators for shape analysis and segmentation. Computers & Graphics, 33, 381–390.

    Article  Google Scholar 

  • Ruggeri, M. R., & Saupe, D. (2008). Isometry-invariant matching of point set surfaces. In Proc. eurographics 2008 workshop on 3D object retrieval.

  • Ruggeri, M. R., Patanè, G., Spagnuolo, M., & Saupe, D. (2009). Spectral-driven isometry-invariant matching of 3D shapes. International Journal of Computer Vision.

  • Rustamov, R. M. (2007). Laplace-Beltrami eigenfunctions for deformation invariant shape representation. In Proc. symp. geometry processing (SGP) (pp. 225–233).

  • Schwartz, E. L., Shaw, A., & Wolfson, E. (1989). A numerical solution to the generalized mapmaker’s problem: flattening nonconvex polyhedral surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 11, 1005–1008.

    Article  Google Scholar 

  • Singh, G., Mémoli, F., & Carlsson, G. (2007). Topological methods for the analysis of high dimensional data sets and 3d object recognition. In Point based graphics, Prague.

  • Spira, A., & Kimmel, R. (2004). An efficient solution to the eikonal equation on parametric manifolds. Interfaces and Free Boundaries, 6(3), 315–327.

    Article  MATH  MathSciNet  Google Scholar 

  • Sun, J., Ovsjanikov, M., & Guibas, L. (2009). A concise and provably informative multi-scale signature based on heat diffusion. In Proc. symp. geometry processing (SGP).

  • Tennenbaum, J. B., de Silva, V., & Langford, J. C. (2000). A global geometric framework for nonlinear dimensionality reduction. Science, 290(5500), 2319–2323.

    Article  Google Scholar 

  • Walter, J., & Ritter, H. (2002). On interactive visualization of high-dimensional data using the hyperbolic plane. In Proc. int’l conf. knowledge discovery and data mining (KDD) (pp. 123–131).

  • Wardetzky, M., Mathur, S., Kälberer, F., & Grinspun, E. (2008). Discrete Laplace operators: no free lunch. In Conf. computer graphics and interactive techniques.

  • Weber, O., Devir, Y. S., Bronstein, A. M., Bronstein, M. M., & Kimmel, R. (2008). Parallel algorithms for approximation of distance maps on parametric surfaces. ACM Transactions on Graphics, 27(4).

  • Wood, Z., Hoppe, H., Desbrun, M., & Schröder, P. (2004). Removing excess topology from isosurfaces. ACM Transactions on Graphics, 23.

  • Yatziv, L., Bartesaghi, A., & Sapiro, G. (2006). O(N) implementation of the fast marching algorithm. Journal of Computational Physics, 212(2), 393–399.

    Article  MATH  Google Scholar 

  • Zhang, H. (2004). Discrete combinatorial Laplacian operators for digital geometry processing. In SIAM conference on geometric design (pp. 575–592).

  • Zigelman, G., Kimmel, R., & Kiryati, N. (2002). Texture mapping using surface flattening via multi-dimensional scaling. IEEE Transactions Visualization and Computer Graphics (TVCG), 9(2), 198–207.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel

    Alexander M. Bronstein, Michael M. Bronstein & Ron Kimmel

  2. Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, USA

    Mona Mahmoudi & Guillermo Sapiro

Authors
  1. Alexander M. Bronstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael M. Bronstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ron Kimmel
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mona Mahmoudi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guillermo Sapiro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guillermo Sapiro.

Additional information

This paper is dedicated to Prof. Gromov in the occasion of receiving the Abel Prize in May 2009.

This work is partially supported by NSF, ONR, NGA, ARO, DARPA, NIH, and by the Israel Science Foundation (ISF grant No. 623/08).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bronstein, A.M., Bronstein, M.M., Kimmel, R. et al. A Gromov-Hausdorff Framework with Diffusion Geometry for Topologically-Robust Non-rigid Shape Matching. Int J Comput Vis 89, 266–286 (2010). https://doi.org/10.1007/s11263-009-0301-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11263-009-0301-6

Keywords

Search

Navigation