Skip to main content
SpringerLink
Log in

Periodic Boundary-Value Problem for a Rayleigh-Type Equation Unsolved with Respect to the Derivative

  • Published:
Ukrainian Mathematical Journal Aims and scope

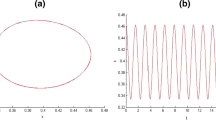
We establish constructive necessary and sufficient conditions of solvability and propose a scheme for the construction of solutions to a nonautonomous nonlinear periodic boundary-value problem for a Rayleightype equation unsolved with respect to the derivative. The urgency of investigation of nonautonomous boundary-value problems unsolved with respect to the derivative is explained by the fact that the analysis of traditional problems solved with respect to the derivative is sometimes significantly complicated, e.g., in the presence of nonlinearities that are not integrable in elementary functions. We consider the critical case in which the equation for generating amplitudes of a weakly nonlinear periodic boundary-value problem for a Rayleigh-type equation does not turn into the identity. The least-squares method is used to establish constructive conditions for the solvability and propose convergent iterative schemes for the construction of approximate solutions to a nonautonomous nonlinear boundary-value problem unsolved with respect to the derivative. As an example of application of the proposed iterative scheme, we find approximations to the solutions of periodic boundary-value problems unsolved with respect to the derivative in the case of periodic problem for the equation that describes the motion of a satellite on the elliptic orbit. We obtain an estimate for the range of values of a small parameter in which the iterative procedure used for the construction of solutions to a weakly nonlinear periodic boundary-value problem for a Rayleigh-type equation unsolved with respect to the derivative is convergent. To check the accuracy of the proposed approximations, we estimate the discrepancies appearing in the equation used to simulate the motion of satellites along the elliptic orbits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. F. Zaitsev and A. D. Polyanin, A Handbook on Nonlinear Ordinary Differential Equations [in Russian], Faktorial, Moscow (1997).

    Google Scholar 

  2. Yu. D. Shlapak, “Periodic solutions of nonlinear second-order equations which are not solved for the highest derivative,” Ukr. Mat. Zh., 26, No. 6, 850–854 (1974); English translation: Ukr. Math. J., 26, No. 6, 702–706 (1974).

  3. A. M. Samoilenko, S. M. Chuiko, and O. V. Nesmelova, “Nonlinear boundary-value problems unsolved with respect to the derivative,” Ukr. Mat. Zh., 72, No. 8, 1106–1118 (2020); English translation: Ukr. Math. J., 72, No. 8, 1280–1293 (2021).

  4. A. A. Boichuk and A. M. Samoilenko, Generalized Inverse Operators and Fredholm Boundary-Value Problems, de Gruyter, Berlin (2016).

    Book  Google Scholar 

  5. A. P. Torzhevskii, “Periodic solutions of the equation of plane oscillations of a satellite on the elliptic orbit,” Kosm. Issled., 2, No. 5, 667–678 (1964).

    Google Scholar 

  6. S. M. Chuiko and O. V. Nesmelova (Starkova), “Autonomous Noether boundary-value problems not solved with respect to the derivative,” J. Math. Sci., 230, No. 5, 799–803 (2018).

  7. D. Nucez and P. J. Torres, “Stable odd solutions of some periodic equations modeling satellite motion,” J. Math. Anal., 279, No. 2, 700–709 (2003).

    Article  MathSciNet  Google Scholar 

  8. A. Cabada and A. J. A. Cid, “On a class of singular Sturm–Liouville periodic boundary value problems,” Nonlin. Anal. Real World Appl., 12, No. 4, 2378–2384 (2011).

    Article  MathSciNet  Google Scholar 

  9. L. V. Kantorovich and G. P. Akilov, Functional Analysis [in Russian], Nauka, Moscow (1977).

    Google Scholar 

  10. S. M. Chuiko, “To the generalization of the Newton–Kantorovich theorem,” Visn. Karazin Kharkiv Nats. Univ., Ser. Mat., Prykl. Mat. Mekh., 85, No. 1, 62–68 (2017).

  11. N. I. Akhiezer, Lectures on Approximation Theory [in Russian], Nauka, Moscow (1965).

    Google Scholar 

  12. S. M. Chuiko, “On approximate solution of boundary-value problems by the least squares method,” Nelin. Kolyv., 11, No. 4, 554–573 (2008); English translation: Nonlin. Oscilat., 11, No. 4, 585–604 (2008).

  13. I. G. Malkin, Some Problems of the Theory of Nonlinear Oscillations [in Russian], Gostekhizdat, Moscow (1956).

    Google Scholar 

  14. G. T. Gilbert, “Positive definite matrices and Sylvester’s criterion,” Amer. Math. Monthly, 98, No. 1, 44–46 (1991).

    Article  MathSciNet  Google Scholar 

  15. S. M. Chuiko, “Domain of convergence of an iterative procedure for an autonomous boundary-value problem,” Nelin. Kolyv., 9, No. 3, 416–432 (2006); English translation: Nonlinear Oscillat., 9, No. 3, 405–422 (2006).

  16. S. Chuiko, “Weakly nonlinear boundary value problem for a matrix differential equation,” Miskolc Math. Notes, 17, No. 1, 139–150 (2016).

    Article  MathSciNet  Google Scholar 

  17. S. M. Chuiko and A. S. Chuiko, “On approximate solution of periodic boundary-value problems with delay by the least-squares method in the critical case,” Nelin. Kolyv., 14, No. 3, 419–432 (2011); English translation: Nonlin. Oscillat., 14, No. 3, 445–460 (2012).

  18. G. V. Demidenko and S. V. Uspensky, Equations and Systems Unsolved with Respect to the Derivative [in Russian], Nauch. Kniga, Novosibirsk (1998).

    Google Scholar 

  19. A. F. Filippov, “Uniqueness of the solution of a system of differential equations unsolved for the derivatives,” Different. Equat., 41, No. 1, 90–95 (2005).

    Article  Google Scholar 

  20. A. V. Arutyunov, E. S. Zhukovskii, and S. E. Zhukovskii, “On the well-posedness of differential equations unsolved for the derivative,” Different. Equat., 47, No. 11, 1541–1555 (2011).

    Article  Google Scholar 

  21. S. M. Chuiko, O. V. Starkova, and O. E. Pirus, “Nonlinear Noetherian boundary-value problems unsolved with respect to the derivative,” Dinam. Sist., 2(30), No. 1-2, 169–186 (2012).

  22. A. A. Boichuk and A. A. Pokutnyi, “Perturbation theory of operator equations in the Fréchet and Hilbert spaces,” Ukr. Mat. Zh., 67, No. 9, 1181–1188 (2015); English translation: Ukr. Math. J., 67, No. 9, 1327–1335 (2016).

  23. O. A. Boichuk and O. A. Pokutnyi, Normally Solvable Boundary-Value Problems for Operator-Differential Equations [in Ukrainian], Naukova Dumka, Kyiv (2022).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Donbas State Pedagogic University, Sloviansk, Donetsk Oblast’, Ukraine

    Serhii Chuiko & Olha Nesmelova

  2. Institute of Applied Mathematics and Mechanics, National Academy of Sciences of Ukraine, Sloviansk, Donetsk Oblast’, Ukraine

    Serhii Chuiko & Olha Nesmelova

Authors
  1. Serhii Chuiko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Olha Nesmelova
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 75, No. 10, pp. 1429–1440, October, 2023. Ukrainian https://doi.org/10.37863/umzh.v75i10.7362.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chuiko, S., Nesmelova, O. Periodic Boundary-Value Problem for a Rayleigh-Type Equation Unsolved with Respect to the Derivative. Ukr Math J 75, 1621–1633 (2024). https://doi.org/10.1007/s11253-024-02282-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-024-02282-2

Search

Navigation