Skip to main content
SpringerLink
Log in

New Results on the Qualitative Analysis of Solutions of Vides by the Lyapunov–Razumikhin Technique

  • Published:
Ukrainian Mathematical Journal Aims and scope

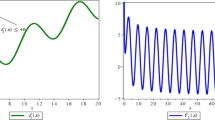
A new mathematical model described by a Volterra integrodifferential equation (VIDE) with constant delay is examined. New agreeable conditions on the uniformly asymptotic stability, boundedness, and square integrability of solutions of the VIDE are obtained by using the Lyapunov–Razumikhin technique. The established conditions improve some former results. They can be also regarded as nonlinear generalizations of these results. Moreover, they are weaker than some available results cited in the bibliography. Two examples are presented to demonstrate possible applications of these results and the introduced concepts. The application of the Lyapunov–Razumikhin technique leads to a significant difference and gives certain advantages over the related methods used in the books and papers cited in the bibliography.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. C. Becker, “Uniformly continuous L1 solutions of Volterra equations and global asymptotic stability,” Cubo, 11, No. 3, 1–24 (2009).

    MathSciNet  MATH  Google Scholar 

  2. T. A. Burton, “Volterra integral and differential equations, 2nd ed.,” Mathematics in Science and Engineering, vol. 202, Elsevier, Amsterdam (2005).

  3. X. Chang and R. Wang, “Stability of perturbed n-dimensional Volterra differential equations,” Nonlin. Anal., 74, No. 5, 1672–1675 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  4. P. Eloe, M. Islam, and B. Zhang, “Uniform asymptotic stability in linear Volterra integro-differential equations with application to delay systems,” Dynam. Systems Appl., 9, No. 3, 331–344 (2000).

    MathSciNet  MATH  Google Scholar 

  5. M. Funakubo, T. Hara, and S. Sakata, “On the uniform asymptotic stability for a linear integro-differential equation of Volterra type,” J. Math. Anal. Appl., 324, No. 2, 1036–1049 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  6. J. R. Graef and C. Tunç, “Continuability and boundedness of multi-delay functional integro-differential equations of the second order,” Rev. R. Acad. Cienc. Exactas Fıs. Nat. Ser. A Math. RACSAM, 109, No. 1, 169–173 (2015).

  7. J. R. Graef, C. Tunç, and S. Şevgin, “Behavior of solutions of nonlinear functional Volterra integro-differential equations with multiple delays,” Dynam. Syst. Appl., 25, No. 1-2, 39–46 (2016).

    MathSciNet  MATH  Google Scholar 

  8. J. Hale, “Theory of functional differential equations, second ed.,” Applied Mathematical Sciences, vol. 3, Springer-Verlag, New York–Heidelberg (1977).

  9. T. Hara, T. Yoneyama, and T. Itoh, “Asymptotic stability criteria for nonlinear Volterra integro-differential equations,” Funkcial. Ekvac., 33, No. 1, 39–57 (1990).

    MathSciNet  MATH  Google Scholar 

  10. Y. Hino and S. Murakami, “Stability properties of linear Volterra integro-differential equations in a Banach space,” Funkcial. Ekvac., 48, No. 3, 367–392 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  11. C. Tunç, “Stability and boundedness in Volterra integro-differential equations with delay,” Dynam. Syst. Appl., 26, No. 1, 121–130 (2017).

    MathSciNet  MATH  Google Scholar 

  12. M. N. Islam and M. M. G. Al-Eid, “Boundedness and stability in nonlinear Volterra integro-differential equations,” PanAmer. Math. J., 14, No. 3, 49–63 (2004).

    MathSciNet  MATH  Google Scholar 

  13. N. N. Krasovskii, Stability of Motion. Applications of Lyapunov’s Second Method to Differential Systems and Equations with Delay, Stanford Univ. Press, Stanford, CA (1963).

  14. S. G. Krein and I. V. Sapronov, “One class of solutions of the Volterra equation with regular singularity,” Ukr. Mat. Zh., 49, No. 3, 424–432 (1997); English translation: Ukr. Math. J., 49, No. 3, 467–476 (1998).

  15. V. Lakshmikantham and M. Rama Mohana Rao, “Theory of integro-differential equations,” Stability and Control: Theory, Methods and Applications, Vol. 1, Gordon & Breach Sci. Publ., Lausanne (1995).

  16. Yu. S. Mishura, “Existence of solutions of abstract Volterra equations in a Banach space and its subsets,” Ukr. Mat. Zh., 52, No. 5, 648–657 (2000); English translation: Ukr. Math. J., 52, No. 5, 741–753 (2001).

  17. Y. Raffoul, “Boundedness in nonlinear functional differential equations with applications to Volterra integro-differential equations,” J. Integral Equat. Appl., 16, No. 4, 375–388 (2004).

    Article  MATH  Google Scholar 

  18. Y. Raffoul, “Exponential stability and instability in finite delay nonlinear Volterra integro-differential equations,” Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 20, No. 1, 95–106 (2013).

  19. R. Reissig, G. Sansone, and R. Conti, Nonlinear Differential Equations of Higher Order, Noordhoff International Publ., Leyden (1974).

    MATH  Google Scholar 

  20. A. M. Samoilenko and N. A. Perestyuk, “Impulsive differential equations. With a preface by Yu. A. Mitropol’skii and a supplement by S. I. Trofimchuk,” World Sci. Ser. Nonlinear Sci. Ser. A Monogr. Treatises, Vol. 14, World Scientific Publ. Co., Inc., River Edge, NJ (1995).

  21. A. M. Samoilenko, O. A. Boichuk, and S. A. Krivosheya, “Boundary-value problems for systems of linear integro-differential equations with a degenerate kernel,” Ukr. Mat. Zh., 48, No. 11, 1576–1579 (1996); English translation: Ukr. Math. J., 48, No. 11, 1785–1789 (1997).

  22. C. Tunç, “Properties of solutions to Volterra integro-differential equations with delay,” Appl. Math. Inf. Sci., 10, No. 5, 1775–1780 (2016).

    Article  Google Scholar 

  23. C. Tunç, “Qualitative properties in nonlinear Volterra integro-differential equations with delay,” J. Taibah Univ. Sci., 11, No. 2, 309–314 (2017).

    Article  Google Scholar 

  24. C. Tunç, “Asymptotic stability and boundedness criteria for nonlinear retarded Volterra integro-differential equations,” J. King Saud Univ.–Sci., 30, No. 4, 3531–3536 (2018).

  25. C. Tunç and O. Tunç, “On behaviors of functional Volterra integro-differential equations with multiple time-lags,” J. Taibah Univ. Sci., 12, No. 2, 173–179 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  26. C. Tunç and O. Tunç, “New results on the stability, integrability and boundedness in Volterra integro-differential equations,” Bull. Comput. Appl. Math., 6, No. 1, 41–58 (2018).

    MathSciNet  MATH  Google Scholar 

  27. C. Tunç and O. Tunç, “New qualitative criteria for solutions of Volterra integro-differential equations,” Arab J. Basic Appl. Sci., 25, No. 3, 158–165 (2018).

    Article  MATH  Google Scholar 

  28. C. Tunç and O. Tunç, “A note on the qualitative analysis of Volterra integro-differential equations,” J. Taibah Univ. Sci., 13, No. 1, 490–496 (2019).

    Article  Google Scholar 

  29. J. Vanualailai and S. Nakagiri, “Stability of a system of Volterra integro-differential equations,” J. Math. Anal. Appl., 281, No. 2, 602–619 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  30. Ke Wang, “Uniform asymptotic stability in functional-differential equations with infinite delay,” Ann. Different. Equat., 9, No. 3, 325–335 (1993).

    MathSciNet  MATH  Google Scholar 

  31. Q. Wang, “The stability of a class of functional differential equations with infinite delays,” Ann. Different. Equat., 16, No. 1, 89–97 (2000).

    MathSciNet  MATH  Google Scholar 

  32. A. M. Wazwaz, Linear and Nonlinear Integral Equations. Methods and Applications, Higher Education Press, Beijing; Springer, Heidelberg (2011).

    Book  MATH  Google Scholar 

  33. Anshi Xu, “Uniform asymptotic stability in functional-differential equations with infinite delay,” Chinese Sci. Bull., 43, No. 12, 1000–1003 (1998).

    Article  MathSciNet  MATH  Google Scholar 

  34. B. Zhou and A.V. Egorov, “Razumikhin and Krasovskii stability theorems for time-varying time-delay systems,” Automat. J. IFAC, 71, 281–291 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  35. M. Bohner, O. Tunç, and C. Tunç, “Qualitative analysis of Caputo fractional integro-differential equations with constant delays,” Comput. Appl. Math., 40, No. 6, Paper 214 (2021).

  36. C. Tunç and A. K. Golmankhaneh, “On stability of a class of second alpha-order fractal differential equations,” AIMS Math., 5, No. 3, 2126–2142 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  37. O. Tunç, “Stability, instability, boundedness and integrability of solutions of a class of integro-delay differential equations,” J. Nonlinear Convex Anal., 23, No. 4, 801–819 (2022).

    MathSciNet  MATH  Google Scholar 

  38. C. Tunç and O. Tunç, “New results on the qualitative analysis of integro-differential equations with constant time-delay,” J. Nonlin. Convex Anal., 23, No. 3, 435–448 (2022).

    MathSciNet  MATH  Google Scholar 

  39. C. Tunç and O. Tunç, “On the stability, integrability and boundedness analyses of systems of integro-differential equations with time-delay retardation,” Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM, 115, No. 3, Paper 115 (2021).

  40. O. Tunç and C. Tunç, “Solution estimates to Caputo proportional fractional derivative delay integro-differential equations,” Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM, 117, No. 1, Paper 12 (2023).

Download references

Author information

Authors and Affiliations

  1. Van Yuzuncu Yil University, Van, Turkey

    O. Tunç

  2. Muş Alparslan University, Muş, Turkey

    E. Korkmaz

Authors
  1. O. Tunç
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Korkmaz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. Tunç.

Additional information

Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 74, No. 11, pp. 1544–1557, November, 2022. Ukrainian DOI https://doi.org/10.37863/umzh.v74i11.6083.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tunç, O., Korkmaz, E. New Results on the Qualitative Analysis of Solutions of Vides by the Lyapunov–Razumikhin Technique. Ukr Math J 74, 1764–1779 (2023). https://doi.org/10.1007/s11253-023-02169-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-023-02169-8

Search

Navigation