Skip to main content
SpringerLink
Log in

Approximations of the Mittag-Leffler Operator Function with Exponential Accuracy and Their Applications to Solving Evolutionary Equations with Fractional Time Derivative

  • Published:
Ukrainian Mathematical Journal Aims and scope

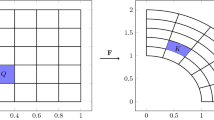
We propose and analyze an efficient discretization of the Mittag-Leffler operator function

$$ {E}_{1+\alpha}\left(-{At}^{1+\alpha}\right)=\sum_{K=0}^{\infty}\frac{{\left(-{At}^{1+\alpha}\right)}^K}{\Gamma \left(1+K\left(1+\alpha \right)\right)}, $$

where A is a self-adjoint positive-definite operator. This function has a broad field of applications. Thus, it specifies a solution operator for the evolutionary problem ∂tu + ∂t−𝛼 Au = 0, t > 0, u(0) = u0, that includes a spatial operator A and its fractional time derivative of order 𝛼 (in the Riemann–Liouville sense), i.e., u(t) = E1+𝛼(−At1+𝛼)u0. We apply the method of Cayley transform, which allows us to recursively separate the variables and represent the Mittag-Leffler function in the form of an infinite series of products of the Laguerre–Cayley functions with respect to the time variable (i.e., polynomials in t1+𝛼) and the powers of Cayley transform for the spatial operator. The approximate representation has the form of a truncated series with N terms. We estimate the accuracy of the N-term approximation scheme depending on 𝛼 and N.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. I. Akhieser and I. M. Glazman, Theory of Linear Operators in Hilbert Space, Pitman (Advanced Publishing Program), Boston, Mass.-London (1980).

  2. D. Z. Arov and I. P. Gavrilyuk, “A method for solving initial value problems for linear differential equations in Hilbert space based on the Cayley transform,” Numer. Funct. Anal. Optim., 14, No. 5-6, 456–473 (1993).

    Article  MathSciNet  MATH  Google Scholar 

  3. A. Ashyralyev, “A note on fractional derivatives and fractional powers of operators,” J. Math. Anal. Appl., 357, No. 1, 232–236 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  4. D. Z. Arov, I. P. Gavrilyuk, and V. L. Makarov, “Representation and approximation of solution of initial value problems for differential equations in Hilbert space based on the Cayley transform,” Elliptic and parabolic problems (Pont-`a-Mousson, 1994), Pitman Res. Notes Math. Ser., 325, 40–50 (1995).

  5. H. Bateman and A. Erdelyi, Higher Transcendental Functions, Vol. 2, MC Graw-Hill Book Co., New York–Toronto–London (1988).

  6. R. Gorenflo, F. Mainardi, and S. Rogosin, “Mittag-Leffler function: properties and applications,” in: Handbook of Fractional Calculus with Applications, Vol. 1, De Gruyter, Berlin (2019), pp. 269–296.

  7. I. P. Gavrilyuk and V. L. Makarov, “Explicit and approximate solutions of second order evolution differential equations in Hilbert space,” Numer. Methods Partial Different. Equat., 15, 111–131 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  8. I. Gavrilyuk, V. Makarov, and V. Vasylyk, Exponentially Convergent Algorithms for Abstract Differential Equations, Birkhäuser/Springer Basel AG, Basel (2011).

    Book  MATH  Google Scholar 

  9. I. P. Gavrilyuk, “Strongly P-positive operators and explicit representations of the solutions of initial value problems for second order differential equations in Banach space,” J. Math. Anal. Appl., 236, No. 2, 327–349 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  10. I. P. Gavrilyuk, “Super exponentially convergent approximation to the solution of the Schrödinger equation in abstract setting,” Comput. Methods Appl. Math., 10, No. 4, 345–358 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  11. I. P. Gavrilyuk, “An algorithmic representation of fractional powers of positive operators,” Numer. Funct. Anal. Optim., 17, No. 3-4, 293–305 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  12. I. P. Gavrilyuk,W. Hackbusch, and B. N. Khoromskij, “Hierarchical tensor-product approximation to the inverse and related operators for high-dimensional elliptic problems,” Computing, 74, No. 2, 131–157 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  13. I. P. Gavrilyuk and B. N. Khoromskij, “Quasi-optimal rank-structured approximation to multidimensional parabolic problems by Cayley transform and Chebyshev interpolation,” Comput. Methods Appl. Math., 191, No. 1, 55–71 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  14. I. P. Gavrilyuk and V. L. Makarov, “Exact and approximate solutions of some operator equations based on the Cayley transform,” Linear Algebra Appl., 282, No. 1-3, 97–121 (1998).

    Article  MathSciNet  MATH  Google Scholar 

  15. I. P. Gavrilyuk and V. L. Makarov, “Representation and approximation of the solution of an initial value problem for a first order differential equation in Banach space,” Z. Anal. Anwend., 15, No. 2, 495–527 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  16. I. P. Gavrilyuk, V. L. Makarov, and V. B. Vasylyk, “Exponentially convergent method for abstract integro-differential equation with the fractional Hardy–Titchmarsh integral,” Dop. Nats. Akad. Nauk Ukr. Mat. Prirodozn. Tekh. Nauki, No. 1, 3–8 (2021).

  17. V. Havu and J. Malinen, “The Cayley transform as a time discretization scheme,” Numer. Funct. Anal. Optim., 28, No. 7-8, 825–851 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  18. H. J. Haubold, A. M. Mathai, and R. K. Saxena, “Mittag-Leffler functions and their applications,” J. Appl. Math., 2011, Article ID 298628, (2011); DOI:https://doi.org/10.1155/2011/298628.

    Article  MathSciNet  MATH  Google Scholar 

  19. W. McLean and V. Thomèe, “Numerical solution via Laplace transform of a fractional order evolution equation,” J. Integr. Equat. Appl., 22, No. 1, 57–94 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  20. G. M. Mittag-Leffler, “Sur la nouvelle fonction E𝛼(z),” C. R. Acad. Sci., 137, 554–558 (1903).

    MATH  Google Scholar 

  21. G. H. Hardy and E. C. Titchmarsh, “An integral equation,” Math. Proc. Cambridge Philos. Soc., 28, No. 2, 165–173 (1932).

    Article  MATH  Google Scholar 

  22. B. Jin, R. Lazarov, and Z. Zhou, “An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data,” IMA J. Numer. Anal., 62, 1–25 (2015).

    Google Scholar 

  23. H.-J. Seybold and R. Hilfer, “Numerical algorithm for calculating the generalized Mittag-Leffler function,” SIAM J. Numer. Anal., 47, No. 1, 69–88 (2008/2009).

  24. P. K. Suetin, Classical Orthogonal Polynomials [in Russian], Nauka, Moscow (1979).

    MATH  Google Scholar 

  25. G. Szegö, Orthogonal Polynomials, American Mathematical Society, Providence, R.I. (1959).

Download references

Author information

Authors and Affiliations

  1. University of Cooperative Education Gera-Eisenach, Eisenach, Germany

    I. P. Gavrilyuk

  2. Institute of Mathematics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    V. L. Makarov

Authors
  1. I. P. Gavrilyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. L. Makarov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. L. Makarov.

Additional information

Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 74, No. 5, pp. 620–634, May, 2022. Ukrainian DOI: https://doi.org/10.37863/umzh.v74i5.7097.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gavrilyuk, I.P., Makarov, V.L. Approximations of the Mittag-Leffler Operator Function with Exponential Accuracy and Their Applications to Solving Evolutionary Equations with Fractional Time Derivative. Ukr Math J 74, 709–725 (2022). https://doi.org/10.1007/s11253-022-02096-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-022-02096-0

Search

Navigation