Skip to main content
SpringerLink
Log in

Radii of Starlikeness and Convexity of the Derivatives of Bessel Function

  • Published:
Ukrainian Mathematical Journal Aims and scope

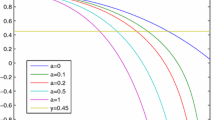
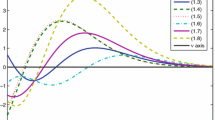
We find the radii of starlikeness and convexity of the derivatives of Bessel function for three different kinds of normalization. The key tools in the proof of our main results are the Mittag-Leffler expansion for the nth derivative of the Bessel function and the properties of its real zeros. In addition, by using the Euler–Rayleigh inequalities we obtain some tight lower and upper bounds for the radii of starlikeness and convexity of order zero for the normalized nth derivative of the Bessel function. As the main results of our investigations, we can mention natural extensions of some known results for the classical Bessel functions of the first kind.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. İ. Aktaş, Á. Baricz, and N. Yağmur, “Bounds for the radii of univalence of some special functions,” Math. Inequal. Appl., 20, 825–843 (2017).

    MathSciNet  MATH  Google Scholar 

  2. İ Aktaş, Á. Baricz, and H. Orhan, “Bounds for radii of starlikeness and convexity of some special functions,” Turkish J. Math., 42, 211–226 (2018).

    Article  MathSciNet  Google Scholar 

  3. Á. Baricz, P. A. Kupán, and R. Szász, “The radius of starlikeness of normalized Bessel functions of the first kind,” Proc. Amer. Math. Soc., 142, No. 6, 2019–2025 (2011).

    Article  MathSciNet  Google Scholar 

  4. Á. Baricz and R. Szász, “The radius of convexity of normalized Bessel functions of the first kind,” Anal. Appl. (Singap.), 12, No. 5, 485–509 (2014).

    Article  MathSciNet  Google Scholar 

  5. Á. Baricz and R. Szász, “The radius of convexity of normalized Bessel functions,” Anal. Math., 41, No. 3, 141–151 (2015).

    Article  MathSciNet  Google Scholar 

  6. Á. Baricz, D. K. Dimitrov, H. Orhan, and N. Yağmur, “Radii of starlikeness of some special functions,” Proc. Amer. Math. Soc., 144, No. 8, 3355–3367 (2016).

    Article  MathSciNet  Google Scholar 

  7. Á. Baricz, H. Orhan, and R. Szász, “The radius of 𝛼-convexity of normalized Bessel functions of the first kind,” Comput. Meth. Funct. Theory, 16, No. 1, 93–103 (2016).

    Article  MathSciNet  Google Scholar 

  8. Á. Baricz, C. G. Kokologiannaki, and T. K. Pogány, “Zeros of Bessel function derivatives,” Proc. Amer. Math. Soc., 146, 209–222 (2018).

    Article  MathSciNet  Google Scholar 

  9. M. Biernacki and J. Krzyż, “On the monotonity of certain functionals in the theory of analytic function,” Ann. Univ. Maria Curie- Skłodowska, Sec. A, 9, 135–147 (1995).

    MathSciNet  MATH  Google Scholar 

  10. R. K. Brown, “Univalence of Bessel functions,” Proc. Amer. Math. Soc., 11, No. 2, 278–283 (1960).

    Article  MathSciNet  Google Scholar 

  11. M. Çağlar, E. Deniz, and R. Szász, “Radii of 𝛼-convexity of some normalized Bessel functions of the first kind,” Results Math., 72, 2023–2035 (2017).

    Article  MathSciNet  Google Scholar 

  12. E. Deniz and R. Szász, “The radius of uniform convexity of Bessel functions,” J. Math. Anal. Appl., 453, No. 1, 572–588 (2017).

    Article  MathSciNet  Google Scholar 

  13. M. E. H. Ismail and M. E. Muldoon, “Bounds for the small real and purely imaginary zeros of Bessel and related functions,” Meth. Appl. Anal., 2, No. 1, 1–21 (1995).

    Article  MathSciNet  Google Scholar 

  14. J. L. W. V. Jensen, “Recherches sur la théorie des équations,” Acta Math., 36, 181–195 (1913).

    Article  MathSciNet  Google Scholar 

  15. C. G. Kokologiannaki and E. N. Petropoulou, “On the zeros of J”' (x),” Integral Transforms Spectr. Funct., 24, No. 7, 540–547 (2013).

  16. E. Kreyszig and J. Todd, “The radius of univalence of Bessel functions,” Illinois J. Math., 4, 143–149 (1960).

    Article  MathSciNet  Google Scholar 

  17. B. Y. Levin, “Lectures on entire functions,” Amer. Math. Soc. Transl. Math. Monogr., vol. 150 (1996).

  18. F. W. Olver, D. W. Lozier, R. Boisvert, and C. W. Clark (eds.), NIST Handbook of Mathematical Functions, Cambridge Univ. Press, Cambridge (2010).

    MATH  Google Scholar 

  19. S. Ponnusamy and M. Vuorinen, “Asymptotic expansions and inequalities for hypergeometric functions,” Mathematika, 44, 278–301 (1997).

    Article  MathSciNet  Google Scholar 

  20. R. Szász, “About the radius of starlikeness of Bessel functions of the first kind,” Monatsh. Math., 176, 323–330 (2015).

    Article  MathSciNet  Google Scholar 

  21. G. N. Watson, A Treatise of the Theory of Bessel Functions, Cambridge Univ. Press, Cambridge, UK; Macmillan Company, New York (1944).

Download references

Author information

Authors and Affiliations

  1. Kafkas University, Kars, Turkey

    E. Deniz & S. Kazımoğlu

  2. Erzurum Technical University, Erzurum, Turkey

    M. Çağlar

Authors
  1. E. Deniz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Kazımoğlu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Çağlar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Çağlar.

Additional information

Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 73, No. 11, pp. 1461–1482, November, 2021. Ukrainian DOI: https://doi.org/10.37863/umzh.v73i11.1014.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deniz, E., Kazımoğlu, S. & Çağlar, M. Radii of Starlikeness and Convexity of the Derivatives of Bessel Function. Ukr Math J 73, 1686–1711 (2022). https://doi.org/10.1007/s11253-022-02024-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-022-02024-2

Search

Navigation