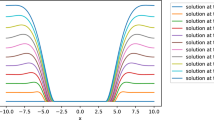
We show that a doubly degenerate thin-film equation obtained in modeling the flows of viscous coatings on spherical surfaces has a finite speed of propagation for nonnegative strong solutions and, hence, there exists an interface or a free boundary separating the regions, where the solution u > 0 and u = 0. By using local entropy estimates, we also establish the upper bound for the rate of propagation of the interface.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
E. Beretta, M. Bertsch, and R. Dal Passo, “Nonnegative solutions of a fourth-order nonlinear degenerate parabolic equation,” Arch. Ration. Mech. Anal., 129, No. 2, 175–200 (1995).
F. Bernis and A. Friedman, “Higher order nonlinear degenerate parabolic equations,” J. Different. Equat., 83, No. 1, 179–206 (1990).
F. Bernis, “Finite speed of propagation and continuity of the interface for thin viscous flows,” Adv. Different. Equat., 1, No. 3, 337–368 (1996).
F. Bernis, “Finite speed of propagation for thin viscous flows when 2 ≤ n < 3,” Compt. Rendus Acad. Sci. Math., 322, No. 12, 1169–1174 (1996).
F. Bernis, L. A. Peletier, and S. M. Williams, “Source type solutions of a fourth order nonlinear degenerate parabolic equation,” Nonlin. Anal., 18, 217–234 (1992).
A. L. Bertozzi, et al., “Singularities and similarities in interface flows,” in: Trends and Perspectives in Applied Mathematics, Springer, New York (1994), pp. 155–208.
M. Chugunova, M. C. Pugh, and R. M. Taranets, “Nonnegative solutions for a long-wave unstable thin film equation with convection,” SIAM J. Math. Anal., 42, No. 4, 1826–1853 (2010).
M. Chugunova and R. M. Taranets, “Qualitative analysis of coating flows on a rotating horizontal cylinder,” Int. J. Different. Equat., Article ID 570283 (2012), 30 p.
A. Friedman, “Interior estimates for parabolic systems of partial differential equations,” J. Math. Mech., 7, No. 3, 393–417 (1958).
J. Hulshof and A. E. Shishkov, “The thin film equation with 2 ≤ n < 3: finite speed of propagation in terms of the L 1-norm,” Adv. Different. Equat., 3, No. 5, 625–642 (1998).
D. Kang, A. Nadim, and M. Chugunova, “Dynamics and equilibria of thin viscous coating films on a rotating sphere,” J. Fluid Mech., 791, 495–518 (2016).
D. Kang, A. Nadim, and M. Chugunova, “Marangoni effects on a thin liquid film coating a sphere with axial or radial thermal gradients,” Phys. Fluids, 29, 072106-1–072106-15 (2017).
D. Kang, T. Sangsawang, and J. Zhang, “Weak solution of a doubly degenerate parabolic equation,” arXiv:1610.06303v2 (2017).
L. Nirenberg, “An extended interpolation inequality,” Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), 20, No. 3, 733–737 (1966).
A. E. Shishkov, “Dynamics of the geometry of the support of the generalized solution of a higher-order quasilinear parabolic equation in the divergence form,” Differents. Uravn., 29, No. 3, 537–547 (1993).
R. M. Taranets, “Strong solutions of the thin-film equation in spherical geometry,” in: V. A. Sadovnichiy and M. Zgurovsky (eds.), Modern Mathematics and Mechanics, Understanding Complex Systems, Springer (2019), pp. 181–192.
D. Takagi and H. E. Huppert, “Flow and instability of thin films on a cylinder and sphere,” J. Fluid Mech., 647, 221–238 (2010).
S. K. Wilson, “The onset of steady Marangoni convection in a spherical geometry,” J. Eng. Math., 28, 427–445 (1994).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Ukrains’kyi Matematychnyi Zhurnal, Vol. 71, No. 6, pp. 840–851, June, 2019.
Rights and permissions
About this article
Cite this article
Taranets, R.M. Finite Speed of Propagation for the Thin-Film Equation in Spherical Geometry. Ukr Math J 71, 956–969 (2019). https://doi.org/10.1007/s11253-019-01690-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-019-01690-z