Abstract
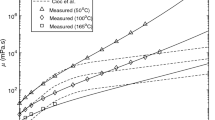
Lubricants which contain a polymeric thickener will often display a second Newtonian plateau in measured flow curves. Like other manifestations of shear-dependent viscosity, this shear response will lead to an inaccurate prediction when the classical film-thickness formulas are employed. A correction formula has been developed from numerical experiments for a range of parameters of the double-Newtonian modified Carreau equation. The parameters of this shear-thinning model were selected from measurements for real lubricants obtained in Couette viscometers and a capillary viscometer. In addition, a full EHL film thickness formula has been derived from the same numerical experiments. The correction formula and the full formula were successfully validated using published film thickness data and published viscosity data for an EHL reference liquid, a polymer solution. Clearly, viscometer measurements of shear-dependent viscosity which contain the inflection leading to the second Newtonian are essential for a film-thickness calculation when a high-molecular-weight component of the lubricant is present.







Similar content being viewed by others
Abbreviations
- a, b, A, B, C :
-
Parameters for correction formulas
- c :
-
Weight fraction of polymer
- E :
-
Combined elastic modulus of the rollers
- F :
-
Load
- G :
-
Effective liquid shear modulus associated with rotational relaxation time
- h :
-
Film thickness
- \( h_{\text{cNewt}} \) :
-
Newtonian solution for central film thickness
- h 0 :
-
Rigid body separation
- H, M, L :
-
Blok dimensionless parameters
- n :
-
Power-law exponent
- \( M_{\text{W}} \) :
-
Molecular weight of polymer
- p :
-
Pressure
- R g :
-
Universal gas constant
- T :
-
Temperature
- U :
-
Surface velocity
- α :
-
Reciprocal asymptotic isoviscous pressure coefficient
- \( \dot{\gamma } \) :
-
Shear rate
- δ :
-
Equivalent elastic deformation
- Γ :
-
Inlet Weissenberg number
- η :
-
Generalized (non-Newtonian) viscosity
- μ :
-
Low shear (first Newtonian) viscosity
- μ 0 :
-
Ambient pressure, low shear viscosity
- μ 2 :
-
Second Newtonian viscosity
- ρ :
-
Mass density
- τ :
-
Shear stress
References
Westlake, F.J., Cameron, A.: Optical elastohydrodynamic fluid testing. ASLE Trans. 15(2), 81–95 (1972)
Hamrock, B.J., Dowson, D.: Isothermal elastohydrodynamic lubrication of point contacts. Part III-fully flooded results. J. Lubr. Technol. 99, 264–276 (1977)
Dalmaz, G., Chaomleffel, J.P.: Elastohydrodynamic lubrication of point contacts for various lubricants. In: Dowson, D., Taylor, C.M., Godet, M., Berthe, D. (eds.) Fluid film lubrication-osborne reynolds centenary, pp. 207–218. Elsevier, Amsterdam (1987)
Villechaise, B., Dalmaz, G., Makala, J., Chaomleffel, J.P.: On the traction fluid behavior in concentrated contacts. In: Dowson, D., Priest, M., Dalmaz, G., Lubrecht, A. (eds.) Boundary and Mixed Lubrication: Science and Applications, pp. 401–412. Elsevier, Amsterdam (2002)
Aderin, M., Johnston, G.J., Spikes, H.A., Caporiccio, G.: The elastohydrodynamic properties of some advanced non hydrocarbon-based lubricants. Lubr. Eng. 48(8), 633–638 (1992)
Bair, S.: High Pressure Rheology for Quantitative Elastohydrodynamics. Elsevier Science, Amsterdam, pp. 29, 143–150, 70, 123 (2007)
Tanner, R.I.: Engineering Rheology, Second Edition. pp. 129–131. Oxford University Press, Oxford (2000)
Bair, S., Lockwood, F.E., Anderson, W.B., Zhang, Z., Dotson, D.: Measurements of elasticity in multigrade motor oil at elevated pressure. STLE Tribol. Trans. 50(3), 407–414 (2007)
Dobson, G.R.: Analysis of high shear rate viscosity data for engine oils. Tribol. Int. 14(4), 195–198 (1981)
Talbot, G.R.: High shear viscometry of concentrated solutions of poly (alkylmethacrylate) in a petroleum lubricating oil. Rheol. Acta 13(2), 305–317 (1974)
Ram, A., Siegman, A.: Intrinsic viscosity of polymer solutions at high shear rates. J. Appl. Polym. Sci. 12(1), 59–69 (1968)
Carreau, P.J.: Rheological equations from molecular network theories. Trans. Soc. Rheol. 16(1), 99–127 (1972)
Bird, R.B., Armstrong, R.C., Hassager, O.: Dynamics of Polymeric Liquids Volume 1 Fluid Mechanics, 2nd edition. p. 144, Wiley, New York (1987)
Bair, S., Khonsari, M.M.: Generalized Reynolds equations for line contact with double-Newtonian shear-thinning. Tribol. Lett. 18(4), 513–520 (2005)
Charles, P., Elfassi, M., Lubrecht, A.A.: Double-Newtonian’ rheological model for the two-dimensional Reynolds equation. Proc. Inst. Mech. Eng. J 225(6), 335–346 (2011)
Bair, S., Winer, W.O.: A simple formula for EHD film thickness of non-Newtonian liquids. In: Dowson, D., Taylor, C.M., Childs, T.H.C., Godet, M., Berthe, D., Dalmaz, G., Berthier, Y., Flamand, L., Georges, J., Lubrecht, A. (eds.) Elastohydrodynamics—’96 Fundamentals and Applications in Lubrication and Traction, pp. 235–241. Elsevier, Amsterdam. (1997)
Bair, S.: Shear thinning correction for rolling/sliding elastohydrodynamic film thickness. Proc. Inst. Mech. Eng. J 219(1), 69–74 (2005)
Kumar, P., Khonsari, M.M.: EHL circular contact film thickness correction factor for shear-thinning fluids. J. Tribol. 130(4), 041506 (2008)
Jang, J.Y., Khonsari, M.M., Bair, S.: Correction factor formula to predict the central and minimum film thickness for shear-thinning fluids in EHL. J. Tribol. 130(2), 024501 (2008)
Anuradha, P., Kumar, P.: New film thickness formula for shear thinning fluids in thin film elastohydrodynamic lubrication line contacts. Proc. Inst. Mech. Eng. J 225(4), 173–179 (2011)
Morales-Espejel, G.E., Wemekamp, A.W.: Ertel–Grubin methods in elastohydrodynamic lubrication—a review. Proc. Inst. Mech. Eng. J 222(1), 15–34 (2008)
Habchi, W., Eyheramendy, D., Vergne, P., Morales-Espejel, G.: Stabilized fully-coupled finite elements for elastohydrodynamic lubrication problems. Adv. Eng. Softw. 46, 4–18 (2012)
Peiran, Y., Shizhu, W.: A generalized Reynolds equation for non-Newtonian thermal elastohydrodynamic lubrication. J. Tribol. 112(4), 631–636 (1990)
Drozd-Rzoska, A., Rzoska, S.J., Roland, C.M., Imre, A.R.: On the pressure evolution of dynamic properties of supercooled liquids. J. Phys. Condens. Matter 20(24), 244103 (2008)
Novak, J.D., Winer, W.O.: Some measurements of high pressure lubricant rheology. J. Lubr. Technol. 90, 580–591 (1968)
Bair, S., Qureshi, F., Kotzalas, M.: The low-shear-stress rheology of a traction fluid and the influence on film thickness. Proc. Inst. Mech. Eng. J 218(2), 95–98 (2004)
Bair, S., Qureshi, F.: The high pressure rheology of polymer-oil solutions. Tribol. Int. 36(8), 637–645 (2003)
Greenwood, J.A.: Film thicknesses in circular elastohydrodynamic contacts. Proc. Inst. Mech. Eng. C 202(1), 11–17 (1988)
Bair, S.: Reference liquids for quantitative elastohydrodynamics: selection and rheological characterization. Tribol. Lett. 22(2), 197–206 (2006)
Bair, S.: Rheology and high-pressure models for quantitative elastohydrodynamics. Proc. Inst. Mech. Eng. J 223(4), 617–628 (2009)
Habchi, W., Eyheramendy, D., Bair, S., Vergne, P., Morales-Espejel, G.: Thermal elastohydrodynamic lubrication of point contacts using a Newtonian/generalized Newtonian lubricant. Tribol. Lett. 30(1), 41–52 (2008)
Acknowledgments
This work was partially supported by the Lubrizol Corporation and by the Center for Compact and Efficient Fluid Power, a National Science Foundation Engineering Research Center funded under cooperative agreement number EEC-0540834. The first author wishes to thank the Council for International Exchange of Scholars (CIES) and the Fullbright commission for funding his visiting scholar program at the Georgia Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
At the time this work was done, the first author was holding a visiting scholar position at Georgia Institute of Technology.
Rights and permissions
About this article
Cite this article
Habchi, W., Bair, S., Qureshi, F. et al. A Film Thickness Correction Formula for Double-Newtonian Shear-Thinning in Rolling EHL Circular Contacts. Tribol Lett 50, 59–66 (2013). https://doi.org/10.1007/s11249-012-0078-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11249-012-0078-6