A Hybrid-Dimensional Coupled Pore-Network/Free-Flow Model Including Pore-Scale Slip and Its Application to a Micromodel Experiment

Abstract

Modeling coupled systems of free flow adjacent to a porous medium by means of fully resolved Navier–Stokes equations is limited by the immense computational cost and is thus only feasible for relatively small domains. Coupled, hybrid-dimensional models can be much more efficient by simplifying the porous domain, e.g., in terms of a pore-network model. In this work, we present a coupled pore-network/free-flow model taking into account pore-scale slip at the local interfaces between free flow and the pores. We consider two-dimensional and three-dimensional setups and show that our proposed slip condition can significantly increase the coupled model’s accuracy: compared to fully resolved equidimensional numerical reference solutions, the normalized errors for velocity are reduced by a factor of more than five, depending on the flow configuration. A pore-scale slip parameter $\beta _{{{{\rm pore}}}}$ required by the slip condition was determined numerically in a preprocessing step. We found a linear scaling behavior of $\beta _{{{{\rm pore}}}}$ with the size of the interface pore body for three-dimensional and two-dimensional domains. The slip condition can thus be applied without incurring any run-time cost. In the last section of this work, we used the coupled model to recalculate a microfluidic experiment where we additionally exploited the flat structure of the micromodel which permits the use of a quasi-3D free-flow model. The extended coupled model is accurate and efficient.

1 Introduction

Coupled systems of free flow over a porous medium play an important role in many environmental, biological and technical processes. Examples include evaporation from soil governed by atmospheric air flow (Vanderborght et al. 2017), intervascular exchange in living tissue (Chauhan et al. 2011), preservation of food (Verboven et al. 2006), fuel cell water management (Gurau and Mann 2009) or heat exchange systems (Yang et al. 2018). Considerable effort has been spent on modeling these kinds of systems where a discrete resolution of the complex porous geometry such as in direct numerical simulation (DNS) is often not computationally feasible for larger systems. The porous medium can instead be treated in an averaged sense, based on the concept of an REV (Whitaker 1999). Following the so-called one-domain approach, one set of equations is used to describe both the free flow and the porous medium (Neale and Nader 1974). For the two-domain approach, a domain decomposition is performed where the free flow is usually described by the Navier–Stokes equations while the porous medium is accounted for by a lower-order model, such as Darcy’s law (Ochoa-Tapia and Whitaker 1995; Layton et al. 2002; Jamet et al. 2009; Mosthaf et al. 2011). Appropriate coupling conditions between the two domains have to be formulated to ensure thermodynamic consistency (Hassanizadeh and Gray 1989). While being computationally efficient, these upscaled models may provide an insufficient degree of detail on the pore scale crucial for certain applications, e.g., when local saturation patterns at the interface of a drying soil globally affect the system (Shahraeeni et al. 2012). For these situations, a new class of so-called hybrid-dimensional models have been developed (Scheibe et al. 2015) which combine the high spatial resolution of pore-scale approaches, such as pore-network models, with the computational efficiency of REV-scale models. Pore-network models simplify the complex void geometry of the porous medium to a collection of equivalent pore elements and provide a comparatively high degree of pore-scale accuracy at low computational demand (Oostrom et al. 2016). Balhoff et al. (2007b) coupled a pore-network model to a Darcy-type continuum model. This concept was further developed (Balhoff et al. 2007a; Mehmani and Balhoff 2014) using mortar methods based on the work of Arbogast et al. (2007). Beyhaghi et al. (2016) proposed an iterative scheme to couple a pore-network model to free flow.

In our previous work (Weishaupt et al. 2019), we have presented a fully monolithic, fully implicit coupled model employing the Navier–Stokes equations in the free-flow region and a pore-network model in the porous domain. The model was verified against numerical reference solutions for stationary single-phase flow and an example of transient compositional flow over a random network was given.

Pores intersecting with the free flow represent local deviations from the no-slip condition which otherwise holds at the solid matrix of the porous medium’s surface. This poses a conceptual weak point of our original model (Weishaupt et al. 2019) where no-slip coupling conditions would always occur at pores with throats oriented normally with the coupling interface. We address this issue here and introduce a pore-local slip condition which helps to correct the momentum exchange between pore-network and free flow.

As in our previous work, we still follow a monolithic coupling approach which does not require any coupling iterations since both sub-problems are solved simultaneously. Here, we further extend the capabilities of the coupled model by removing its former dependency on a direct linear solver. Instead, we now employ an iterative linear solver where an Uzawa method (Ho et al. 2017) serves as a preconditioner for the free-flow matrix blocks. This enhances the model’s applicability to larger and three-dimensional systems while we still benefit from a fully coupled and implicitly mass conservative model formulation.

We assess the accuracy of the novel slip condition and demonstrate the improved model’s capabilities with a three-dimensional numerical example involving a randomly generated pore network.

Finally, we use the coupled model to recalculate high-resolution micro-Particle Image Velocimetry (micro-PIV) experiments performed on a micromodel comprising a free-flow channel over a regular porous structure at low Reynolds numbers (Terzis et al. 2019). Here, we exploit the micromodel’s flat geometry which permits the use of a two-dimensional free-flow model including a wall friction term (Flekkøy et al. 1995) in order to save computational cost.

2 Mathematical and Numerical Model Concepts

Without loss of generality, gravity is neglected in the following and we assume incompressible steady-state flow conditions for sake of simplicity. Creeping flow ($Re < 1$) is considered in this work.

2.1 Free-Flow Model

The Stokes equations are used for the description of incompressible steady-state laminar flow:

$$\nabla \cdot \!{[\mu (\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T})]} -\nabla \!p = 0.$$

(1)

$\mu$ is the fluid’s dynamic viscosity, ${\bf v}$ is the fluid velocity while p is the pressure.

The continuity equation closes the system:

$$\nabla \cdot \!{{\bf v}} = 0.$$

(2)

2.2 Pore-Network Model

In the porous domain, a pore-network model is used where at each pore body (the intersection of two or more pore throats), the continuity of mass is required:

$$\sum _j Q_{ij} = 0.$$

(3)

Here, $Q_{ij}$ is the discrete volume flow rate in a throat connecting pore bodies i and j:

$$Q_{ij} = g_{ij} (p_i - p_j).$$

(4)

$p_i$ and $p_j$ are the pressures defined at the centers of the pores bodies. The throat conductance $g_{ij}$ depends on the pore throat geometry and the fluid properties. For certain geometries, simple analytical expressions for $g_{ij}$ are available in the literature (Patzek and Silin 2001). Otherwise, numerical upscaling (Mehmani and Tchelepi 2017; Weishaupt et al. 2019) may be used.

2.3 Coupling Conditions

Appropriate coupling conditions are required to ensure the continuity of mass and momentum at the interface between porous medium ($\Omega ^{{\rm PNM}}$) and free flow ($\Omega ^{{{\rm FF}}}$) (Hassanizadeh and Gray 1989; Layton et al. 2002). Here, we formulate the coupling conditions for each discrete intersection of a pore body i with the boundary of the free-flow domain, yielding pore-local discrete coupling interfaces $\Gamma _i$.

The coupling pore bodies are cut in half by the interface and only the interior part of the volume is considered. We assume that the coordination number of pore bodies connected to the free-flow domain is always one, i.e, only one pore throat is connected to them.

The conservation of mass (neglecting density since we consider incompressible fluids in this work) across the interface is enforced via

$${[}{\bf v}\cdot {\bf n}]^{{\rm PNM}}= -[{\bf v}\cdot {\bf n}]^{{{\rm FF}}}.$$

(5)

The superscripts ${{{\rm FF}}}$ and ${{\rm PNM}}$ refer to the interfacial quantities of the free-flow domain and the pore-network model, respectively. ${\bf n}$ is a unit vector normal to the coupling interface, pointing out of the own domain.

Compared to Weishaupt et al. (2019), we revise our coupling conditions for the mechanical equilibrium, i.e., the conservation of momentum across the interface. We first recall that Eq. (4), which yields the discrete volume flow per pore throat in the pore-network model, is based on the volume integration of the three-dimensional Stokes equations along the medial axis of the pore throat (Blunt 2017). Contrary to Darcy-type models (Whitaker 1999; Layton et al. 2002), the pore body pressure of the pore-network model and the pressure of the Stokes model employed in the free-flow region have thus a comparative physical meaning. Therefore, we require the pressures at the interface to be equal in order to satisfy the balance of forces perpendicular to the interface:

$${[}p]^{{{\rm FF}}}= [p]^{{\rm PNM}}.$$

(6)

At the location of solid grains (no intersecting pore throat), a no-flow/no-slip condition for the free flow is assumed. Weishaupt et al. (2019) used the tangential component of the discrete pore velocity as a coupling condition for the free-flow model at the location of the intersecting pore:

$$\begin{aligned} {[}{\bf v}\cdot {\bf t}_k]^{{{{\rm FF}}}} = {\left\{ \begin{array}{ll} {[} {\bf v}\cdot {\bf t}_k ]^{{{\rm PNM}}} ,&\quad k \in \{0,\ldots ,d-1\} \quad {{\rm on}} ~ \Gamma _i^{{{\rm FF}}}\\ 0 &\quad \text {else}. \end{array}\right. } \end{aligned}$$

(7)

The basis of the interface’s tangent plane is given by ${\bf t}_k,~ k \in \{0,\ldots ,d-1\}$. The tangential component of the pore-body interface velocity is approximated as

$$\begin{aligned} {[}{\bf v}\cdot {\bf t}_k ]^{{\rm PNM}}= \frac{Q_{ij}}{|\Gamma _i^{{{\rm FF}}}|} [ {\bf n}_{{\bf ij}} \cdot {\bf t}_k]^{{\rm PNM}}. \end{aligned}$$

(8)

$Q_{ij}$ is the volume flow through pore throat ij while $|\Gamma _i^{{{\rm FF}}}|$ is the area of the discrete coupling interface. ${\bf n}_{{\bf ij}}$ is a unit normal vector parallel to the throat’s central axis and pointing toward the interface. Note that this is a simplification which does not take into account potential deflection effects of the fluid flow leaving the pore throat and entering the pore body (see Fig. 1a). Note that Eq. (8) does not impair mass conservation as it is only used for the approximation of the tangential momentum transfer.

The disadvantage of Eq. (7) is that pore throats orientated orthogonally with the interface (${\bf n}_{{\bf ij}} \perp [{\bf t}_k]^{\text {FF}}$) will always lead to a no-slip condition such that $[{\bf v}\cdot {\bf t}_k ]^{{{\rm FF}}}= 0$ at the interface since $[{\bf n}_{{\bf ij}} \cdot {\bf t}_k]^{{\rm PNM}}= 0$. The same issue occurs for $Q_{ij} = 0$, yielding $[{\bf v}\cdot {\bf t}_k ]^{{\rm PNM}}= 0$.

Fig. 1

Pore-local slip conditions. Illustration of the two possible interface conditions for $[{\bf v}\cdot {\bf t}_k]^{{{{\rm FF}}}}$ (here with $k =0$). a Old condition (Eq. 7) assigning the pore-body tangential velocity at the interface directly. b Novel slip condition (Eq. 11) allowing $[{\bf v}\cdot {\bf t}_k]^{{{{\rm FF}}}} \ne [{\bf v}\cdot {\bf t}_k]^{{\rm PNM}}$

Here, we propose a modified approach to approximate the slip velocity on $\Gamma _i^{{{\rm FF}}}$ (see Fig. 1b). We require the continuity of tangential stress

$$\begin{aligned} {[}(-\mu (\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}) \cdot {\bf n}) \cdot {\bf t}_k]^{{{{\rm FF}}}} = [(-\mu (\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}) \cdot {\bf n}) \cdot {\bf t}_k]^{{{\rm PNM}}}. \end{aligned}$$

(9)

Instead of trying to calculate the shear rate $\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}$ in the one-dimensional pore throats where only uniform, averaged flows along the center-line of the throats are defined, we use a simple parametrization

$$\begin{aligned} {[}(-(\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}) \cdot {\bf n}) \cdot {\bf t}_k]^{{{{\rm FF}}}} = \beta _{{{\rm throat}}} \frac{[\mu ]^{{\rm PNM}}}{[\mu ]^{{{\rm FF}}}} \left( [{\bf v}\cdot {\bf t}_k]^{{{{\rm FF}}}} - [{\bf v}\cdot {\bf t}_k]^{{{\rm PNM}}} \right) \end{aligned}$$

(10)

in close analogy to the widely used Beavers–Joseph interface slip condition for REV-scale models (Beavers and Joseph 1967; Jones 1973). The main difference here is that the slip coefficient $\beta _{{{{\rm pore}}}}$ is now defined locally per pore and not given as averaged quantity of the entire porous medium’s interface. As we assume a constant and equal viscosity in both domains, the term $\frac{[\mu ]^{{\rm PNM}}}{[\mu ]^{{{\rm FF}}}} = 1$ is dropped for sake of brevity.

Our new coupling condition for the tangential component of the free-flow velocity thus reads

$$\begin{aligned} {[}{\bf v} \cdot {\bf t}_k]^{{{\rm FF}}}= {\left\{ \begin{array}{ll} v_{{{{\rm slip}}},k} &{}\quad \text {on pore throat},\\ 0 &{}\quad \text {else}, \end{array}\right. } \end{aligned}$$

(11)

with

$$\begin{aligned} v_{{{{\rm slip}}},k} = \frac{1}{\beta _{{{{\rm pore}}}}} \left[ (-(\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}) \cdot {\bf n}) \cdot {\bf t}_k \right] ^{{{\rm FF}}}+ \left[ {\bf v} \cdot {\bf t}_k \right] ^{{\rm PNM}}. \end{aligned}$$

(12)

$1/\beta _{{{{\rm pore}}}}$ corresponds to a local Navier slip length (Navier 1823) and is generally a tensorial (Kamrin et al. 2010) and solution-dependent quantity (Yang et al. 2019). For certain geometries and flow configurations, it may be obtained by (semi-) analytical (Jeong 2001; Wang 2003; Schönecker and Hardt 2013) expressions which are, however, mathematically involved and often require numerical methods for their solution at some point. Furthermore, surface-averaged effective values of the slip length for periodic geometries are usually considered (Lauga and Stones 2003) while we require a local value for a single pore.

Since $\beta _{{{{\rm pore}}}}$ is merely an input parameter for our model and the aim of this work is to investigate the benefit of using Eq. (11), we employ a simple numerical procedure to estimate this value as described later on. We will furthermore show that $\beta _{{{{\rm pore}}}}$ scales linearly with the diameter of the intersecting entity for our two- and three-dimensional setups. This implies that Eq. (11) can be applied at zero additional run-time cost, once the scaling factors for the geometries of interest have been determined in a preprocessing step.

2.4 Implementation

The coupled model is implemented in DuMu^x, an open-source framework for simulating flow and transport in porous media (Flemisch et al. 2011; Heck et al. 2019; Koch et al. 2020), built upon dune (Bastian et al. 2008a, b). We use dune-subgrid (Gräser and Sander 2009) for the generation of the reference solution grids and dune-foamgrid (Sander et al. 2017) for the pore-network model.

The free-flow model is discretized in space using a staggered-grid finite volume approach, also known as MAC scheme (Harlow and Welch 1965), which provides inherently stable and oscillation-free solutions without the need of any stabilization techniques (Versteeg and Malalasekera 2007). The original model’s restriction to odd numbers (Weishaupt et al. 2019) of free-flow grid cells assigned to each pore throat has been lifted here.

As in Weishaupt et al. (2019), we follow a fully monolithic coupling concept which means that all sub-models’ balance equations are assembled into one system of linear equations which is solved simultaneously such that no coupling iterations are required and the scheme is inherently conservative:

$$\begin{aligned} \begin{pmatrix} A &{} B_1 &{} C_1\\ B_2 &{} D &{} C_2 \\ C_3 &{} C_4 &{} P \end{pmatrix} \begin{pmatrix} {\bf x}_{v,{{{\rm FF}}}}\\ {\bf x}_{p,{{{\rm FF}}}}\\ {\bf x}_{p,{{\rm PNM}}} \end{pmatrix} =\begin{pmatrix} {\bf r}_{v,{{{\rm FF}}}}\\ {\bf r}_{p,{{{\rm FF}}}}\\ {\bf r}_{p,{{\rm PNM}}} \end{pmatrix}. \end{aligned}$$

(13)

Here, $A, \,B_1, \,B_2$ and D are sub-matrices of the free-flow problem. P is the sub-matrix of the pore-network model and $C_1$–$C_4$ are the coupling matrix blocks. ${\bf x}$ is a sub-vector of unknowns for the velocity v or pressure p and the sub-domains ${{{\rm FF}}}$ (free flow) and ${{\rm PNM}}$ (pore-network model). ${\bf r}$ are the corresponding right-hand side sub-vectors.

Solving this system is challenging for Krylov-type iterative methods as it features a poorly conditioned system matrix including a saddle-point structure for incompressible fluids ($D = 0$) (Benzi et al. 2005). For this reason, we used a direct linear solver in Weishaupt et al. (2019) which, however, does not scale very well in terms of memory and CPU-time requirements for larger systems, especially in 3D. We overcome this limitation here by applying a flexible restarted GMRES iterative solver (Saad 2003) on Eq. (13) which requires appropriate preconditioning.

As a very first step toward an effective solution strategy, a simple Uzawa algorithm (Benzi et al. 2005; Ho et al. 2017) is used for the free-flow sub-system

$$\begin{aligned} \begin{pmatrix} A &{} B_1\\ B_2 &{} D\\ \end{pmatrix} \begin{pmatrix} {\bf x}_{v,{{{\rm FF}}}}\\ {\bf x}_{p,{{{\rm FF}}}}\\ \end{pmatrix} = \begin{pmatrix} {\bf r}_{v,{{{\rm FF}}}}\\ {\bf r}_{p,{{{\rm FF}}}}\\ \end{pmatrix}, \end{aligned}$$

(14)

with

$${\bf x}_{v,{{{\rm FF}}}, m+1}= {\bf x}_{v,{{{\rm FF}}}, m} + A^{-1} \left( {\bf r}_{v,{{{\rm FF}}}} -\left( A {\bf x}_{v,{{{\rm FF}}}, m} + B_1 {\bf x}_{p,{{{\rm FF}}},m} \right) \right) ,$$

(15)

$${\bf x}_{p,{{{\rm FF}}}, m+1} = {} {\bf x}_{p,{{{\rm FF}}}, m} + \omega \left( {\bf r}_{p,{{{\rm FF}}}} - \left( B_2 {\bf x}_{v,{{{\rm FF}}}, m+1} + D {\bf x}_{p,{{{\rm FF}}}, m} \right) \right) .$$

(16)

$A^{-1}$ is approximated using an algebraic multigrid method (Shapira 2008) and $\omega$ is a relaxation factor determined according to Benzi et al. (2005).

A simple Jacobi (diagonal) preconditioner is applied to the pore-network sub-system

$$P {\bf x}_{p,{{\rm PNM}}} = {\bf r}_{p,{{\rm PNM}}}.$$

(17)

The further development of this rather elementary preconditioning strategy is part of ongoing work and techniques such as presented in Kuchta et al. (2018) could certainly improve the solver’s efficiency.

3 Numerical Determination of $\beta _{{{{\rm pore}}}}$ and Assessment of Accuracy

In this section, we present a simple numerical procedure to estimate the pore-scale slip coefficient $\beta _{{{{\rm pore}}}}$ for two different geometries: (1) a hemispherical, three-dimensional pore body and (2) a two-dimensional square cavity.

3.1 Numerical Determination of the Slip Coefficient $\beta _{{{{\rm pore}}}}$

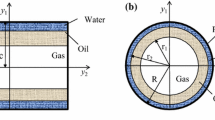
Figure 2 shows the computational domains used to evaluate $\beta _{{{{\rm pore}}}}$: In the three-dimensional setup (Fig. 2a), a hemispherical pore body with radius $r_i$ intersects with the lower bottom of a cubic free-flow channel, whose side lengths $L_x, L_y$ and $L_z$ are ten times larger than $r_i$. For sake of simplicity, we neglected the pore throat adjacent to the pore body and hence, $[{\bf v}]^{{\rm PNM}}\cdot {\bf t}_k = 0$. We will discuss this choice later on. In order to assess the dependence of $\beta _{{{{\rm pore}}}}$ on the pore radius, we performed multiple simulations with different $r_i$ while keeping the overall proportions of the geometry constant (i.e, scaling $L_x = L_y = L_z$ accordingly). $Re \ll 1$ with respect to the channel hydraulic diameter was held for all setups. Flow was induced in two different ways in order to investigate the influence of the boundary conditions on $\beta _{{{{\rm pore}}}}$: first, a pressure drop $\Delta p$ between the inlet on the left side and the outlet on the right side of the channel was assigned which corresponds to a situation typical for micro-PIV experiments. Second, shear-driven flow was considered by moving the top wall of the domain at a given velocity which resembles a near-interface flow field for free or atmospheric flow conditions. Figure 2b shows the two-dimensional setup with a square pore body for which the same procedure as for the 3D setup was performed.

Fig. 2

Setups for the numerical determination of $\beta _{{{{\rm pore}}}}$. The distribution of $v_x$ along the domain’s vertical extent $L_y$ for a pressure-driven flow is sketched by the colored surface (a) and line (b), respectively. The dotted areas mark the pore-local slip interfaces $\Gamma _i$ on which the averaging is performed

Having checked for grid convergence, the domains were meshed uniformly such that 40 cells per pore diameter were used for each simulation. Since $\beta _{{{{\rm pore}}}}$ will later on be used in the coupled model which is implemented in DuMu^x, we also employed the free-flow solver (not being coupled to another model) of the latter for determining $\beta _{{{{\rm pore}}}}$ for sake of comparability. Currently, only structured, axis parallel grids are supported here, but we assured that our results are in accordance with simulations performed on an unstructured grid (allowing a smoother description of the hemispherical cavity’s bottom surface) performed with the open-source CFD tool OpenFOAM (Jasak 2009).

For the pressure-driven cases, all boundaries were equipped with no-flow/no-slip conditions, except at the inlet and the outlet where fixed pressures $p_{{{{\rm in}}}} = 1\times 10^{-6}\,\hbox {Pa}$ and $p_{{{\rm out}}} = 0\,\hbox {Pa}$ were assigned. Preliminary simulations showed that a fully developed flow within the channel (with respect to the x-axis) was achieved this way, without the need of using periodic boundary conditions at the inlet and the outlet (which are not yet supported by the free-flow model in DuMu^x). For the shear-driven setup, we set $p_{{{{\rm in}}}} = p_{{{{\rm out}}}} = 0\,\hbox {Pa}$ and a constant velocity $v_{x,{{{\rm top}}}} = 4 \times 10^{-8}\,\hbox {ms}$ at the top wall of the channel. For the 3D geometry, we eliminated the wall friction on the lateral sides of the free-flow channel ($z_{{{{\rm min}}}}$ and $z_{{{{\rm max}}}}$) by setting symmetry boundary conditions. We solve Eqs. (1) and (2) to obtain the stationary flow field for an incompressible fluid (water) with $\mu = 1\times 10^{-3}\hbox {Pa}\,\hbox {s}$.

In theory, Eq. (12) holds on each point on the local interface between the free-flow channel and the pore $\Gamma _i$ (see Fig. 2) such that the value of $\beta _{{{{\rm pore}}}}$ actually depends on the relative position on $\Gamma _i$. As a simplification for the numerical evaluation of $\beta _{{{{\rm pore}}}}$ and, more importantly, for an efficient application of the slip concept within the coupled model, we instead consider one integral value of $\beta _{{{{\rm pore}}}}$ for each $\Gamma _i$. As mentioned above, $\left[ {\bf v} \cdot {\bf t}_k \right] ^{{\rm PNM}}= 0$ as there is no pore throat attached to the body and $Q_{ij} = 0$ (see Eq. 8). For the given setup (3D), ${\bf n}= (0, -1, 0)^{\rm T}$ and we only consider ${\bf t}_0 = (1,0,0)^{\rm T}$ as the flow is mainly in x-direction. We average the relevant velocity gradients and the streamwise horizontal velocity component $v_{{{{\rm slip}}},0} = \left[ {\bf v} \cdot {\bf t}_0 \right] ^{{{{\rm FF}}}} = \left[ v_x \right] ^{{{\rm FF}}}$ on $\Gamma _i$ in order to estimate $\beta _{{{{\rm pore}}}}$ by re-arranging and simplifying Eq. (12):

$$\begin{aligned} \beta _{{{{\rm pore}}}}\approx \frac{\left\langle \left[ -(\nabla \!{ {\bf v}} + \nabla \!{ {\bf v}}^{\rm T}) \cdot {\bf n}) \cdot {\bf t}_0\right] ^{{{\rm FF}}}\right\rangle }{\langle v_{{{{\rm slip}}},0} \rangle } = \frac{ \left\langle \left[ \frac{\partial v_x }{\partial y} + \frac{\partial v_y }{\partial x} \right] ^{{{\rm FF}}}\right\rangle }{\left\langle \left[ v_x \right] ^{{{\rm FF}}}\right\rangle }. \end{aligned}$$

(18)

Here, $\langle \cdot \rangle$ is a surface average defined on $\Gamma _i$. In this setup, $\beta _{{{{\rm pore}}}}$ is isotropic because $\Gamma _i$ is of symmetric circular shape. For other shapes (such as ovals), the value of $\beta _{{{{\rm pore}}}}$ would depend on the orientation of the pore body relative to the channel-flow direction.

Table 1 Values of $\beta _{{{{\rm pore}}}}$ and $\beta _{{{{\rm pore}}}}^* = \beta _{{{{\rm pore}}}}r_i$ for the 3D hemispherical pore body

The results of $\beta _{{{{\rm pore}}}}$ for the 3D setup with different pore radii $r_i$ are given in Table 1. Non-dimensionalizing these values by multiplication with the respective value of $r_i$ yields a constant value of $\beta _{{{{\rm pore}}}}^* = \beta _{{{{\rm pore}}}}r_i = 5.73$ for pressure-driven flow and $\beta _{{{{\rm pore}}}}^* = 6.44$ for shear flow. The results thus vary by around $12\%$ for different boundary conditions. The linear scaling of $\beta _{{{{\rm pore}}}}$ with respect to $r_i$ for the given setups is a direct consequence of the linear nature of Eq. (1). Using a dimensionless velocity ${\bf v}^* = {\bf v}/ v_{{{\rm ref}}}$ and a dimensionless gradient $\nabla \!^* = L_{{{\rm ref}}} \nabla \!$ (with $v_{{{\rm ref}}}$ and $L_{{{\rm ref}}} = r_i$ as reference velocity and reference length), Eq. (18) can be re-written as

(19)

For our uniformly scaled setups, any change of $L_{{{\rm ref}}}$ yields the same dimensionless velocity field scaled by an appropriate $v_{{{\rm ref}}}$ (we keep the values of $p_{{{\rm in}}}$ and $p_{{{\rm out}}}$ or $v_{x,{{{\rm top}}}}$ fixed). The averaged values of the dimensionless shear rate and slip velocity on $\Gamma _i$ in Eq. (19) are proportional to each other and $\beta _{{{{\rm pore}}}}^*$ becomes a constant for each uniformly scaled setup.

As a next step, we assessed the impact of altering the free-flow channel’s aspect ratio by halving and doubling its vertical size $L_y$ for a pore radius of $r_i = 200\times 10^{-6}\,\hbox {m}$. As shown in the last two rows of Table 1, this leads to a slightly different value of $\beta _{{{{\rm pore}}}}^*$ because this new problem is not just a uniformly scaled variant of the previous setups ($L_y\not = L_x$), as discussed before. The difference is largest for a decrease of $L_y$ in the pressure-driven case ($-4\%$). This is probably due to the rather pronounced change of the parabolic velocity profile within the free-flow channel when reducing its height (while keeping the pressure gradient constant). For the shear-driven flow, increasing $L_y$ does not change $\beta _{{{{\rm pore}}}}^*$, as the linear flow profile in the free-flow channel remains its shape. Reducing $L_y$ for the same flow configuration only slightly ($+0.3\%$) affects $\beta _{{{{\rm pore}}}}^*$.

The same findings as described above generally also hold for the two-dimensional square cavity (see Fig. 2b), for which we repeated the same evaluating steps as for the 3D geometry. Table 2 shows that $\beta _{{{{\rm pore}}}}^*$ for the shear-flow setup is around $4\%$ larger than the value for pressure-driven flow, whereas it again reacts more sensitive to a change of the free-flow channel’s vertical extent ($-3.6\%$ and $2\%$ compared to $L_y / r_i = 10$) in the latter configuration.

Table 2 Values of $\beta _{{{{\rm pore}}}}$ and $\beta _{{{{\rm pore}}}}^* = \beta _{{{{\rm pore}}}}r_i$ for the 2D square pore body

In summary, our very simple and heuristic method to estimate $\beta _{{{{\rm pore}}}}$ has shown that this value scales linearly with the pore diameter, and that the chosen set of boundary conditions mildly affects the results. As shown by Moffatt (1964), a series of diminishing vortices can be observed within the cavity. Compared to the slip velocity on $\Gamma _i$, the intensity of these recirculations is negligible and the vortex structures will be completely overlaid for situations with flow in the adjacent pore throat (Sects. 3.2, 4, 5). We therefore consider our setups as presented in Fig. 2 representative for our further analysis.

As previously mentioned, a direct comparison of our findings for the values of $\beta _{{{{\rm pore}}}}$ with literature values for the Navier slip length is not straightforward because typically, surface-averaged, effective values for periodic structures are reported. However, one can roughly estimate the maximum slip length over a single two-dimensional quadratic cavity by $0.5 r_i$, based on the center position of the first vortex within the cavity (Schönecker and Hardt 2013). This yields a value of $1\times 10^{-4}\,\hbox {m}$ for the cavity with $r_i = 2\times 10^{-4}\,\hbox {m}$ which is therefore around twice as large as our numerically determined mean slip length of $1/\beta _{{{{\rm pore}}}}= 4.36\times 10^{-5}\,\hbox {m}$ (shear-driven flow). We again want to stress that the focus of this paper is not on finding a generalized method for describing $\beta _{{{{\rm pore}}}}$ but rather on evaluating the effect of using the slip condition in the context of our coupled model for which $\beta _{{{{\rm pore}}}}$ serves as an input parameter.

3.2 Evaluation of the Slip Condition’s Accuracy Improvement

Having estimated $\beta _{{{{\rm pore}}}}$ numerically, we investigate the benefit of using the new slip condition (Eq. (11)) in the coupled model compared to Eq. (7), yielding a no-slip condition for throats oriented orthogonally with the interface ($[{\bf v}]^{{\rm PNM}}\cdot [{\bf t}_k]^{{{\rm FF}}}= 0$) or featuring no flow ($[{\bf v}]^{{\rm PNM}}= 0$). For this purpose, we consider a three-dimensional cubic free-flow channel with side lengths of $5\times 10^{-4}\,\hbox {m}$ intersecting with a single pore ($r_i = 1\times 10^{-4}\,\hbox {m}$) and throat ($r_{ij} = 5\times 10^{-5}\,\hbox {m}$). Six different geometrical setups are investigated by varying the throat’s orientation represented by the polar and the azimuth angles ($\theta _{{{\rm pol}}}$ and $\varphi _{{{\rm az}}}$), as shown in Fig. 3. The vertical position of the lower pore body center is fixed at $y = -4\times 10^{-4}\,\hbox {m}$ such that the length of the throat is slightly different for each setup (which is accounted for in the throat’s conductance in Eq. (20)).

We use DuMu^x to solve the stationary Stokes equations (Eqs. 1, 2) on the fully resolved, three-dimensional domains in order to obtain reference solutions. Again, 40 grid cells per pore diameter are employed and water ($\mu = 1\times 10^{-3}\,\hbox {Pa}\,\hbox {s}$) is considered.

Flow is induced in the channel by applying a pressure drop $p_{{{{\rm in}}}} - p_{{{{\rm out}}}} = 1\times 10^{-6}\,\hbox {Pa}$ between the inlet and the outlet, as shown in Fig. 3. The bottom of the lower half-pore is equipped with a fixed pressure of $p_{{{\rm bottom}}}$. No-flow/no-slip conditions hold at all remaining boundaries. We investigate four different flow configurations by varying the ratio between the bottom and the inlet pressure $p_{{{\rm bottom}}} / p_{{{\rm in}}} = \{0.33, 1, 10, 100 \}$. The first ratio of 0.33 corresponds to an extraction, i.e., the liquid is sucked out of the channel through the pore throat. For the remaining three ratios, liquid is injected from the pore throat into the channel.

Fig. 3

Geometry used for error analysis. $\theta _{{{{\rm pol}}}}$ is the polar angle corresponding to the vertical inclination of the throat. The azimuth angle $\varphi _{{{{\rm az}}}}$ corresponds to the horizontal orientation of the throat

Having obtained reference solutions, the coupled model is applied twice to each case, using Eq. (7) or Eq. (11), respectively. We used a numerical upscaling approach in a preprocessing step as described in the appendix of Weishaupt et al. (2019) to determine the throat conductance: a pressure boundary value problem is solved numerically on a discretely resolved, reduced but equivalent pore structure in order to relate the pressure drop within the pore throat and bodies to the resulting volume flow. This yields, for the given geometry,

$$\begin{aligned} g_{ij}(l_{ij}) \approx \frac{1}{\mu } \left( \frac{2.44\times 10^{-18}\,\hbox {m}^{-2}}{l_{ij}} + \frac{2}{5.45\times 10^-14\,\hbox {m}^{3}}\right) ^{-1}. \end{aligned}$$

(20)

Here, $\mu$ and $l_{ij}$ are the fluid’s viscosity and the throat length, excluding the two adjacent pore-body radii. The first term of Eq. (20) differs by less than $1\%$ from the corresponding analytical value for a cylindrical tube. The second term of Eq. (20) accounts for the pressure drop within the two adjacent pore bodies. Following the results of the previous section, we chose $\beta _{{{{\rm pore}}}}= 57 348\,\hbox {m}^{-1}$ according to Table 1.

The benefit of using the novel slip condition in the coupled model is quantified by

$$\begin{aligned} \eta _{\rm v} = \frac{{{{\rm err}}}_{\rm v}^{{{\rm old}}}}{{{{\rm err}}}_{\rm v}^{{{\rm new}}}}, \end{aligned}$$

(21)

where ${{{\rm err}}}_{\rm v}$ is the normalized velocity error norm for the free-flow region (“old” when using Eq. 7 and “new” when using Eq. 11),

$$\begin{aligned} {{{\rm err}}}_{\rm v} = \frac{\Vert \Delta {\bf v} \Vert _2}{\Vert {\bf v}_{{{\rm ref}}} \Vert _2} = \frac{\left( \sum _i (\Delta v_{x}^2 + \Delta v_{y}^2 + \Delta v_{z}^2)_i \right) ^{1/2}}{\left( \sum _i (v_{{{{\rm ref}}},x}^2 + v_{{{{\rm ref}}},y}^2 + v_{{{{\rm ref}}},z}^2)_i \right) ^{1/2}}. \end{aligned}$$

(22)

${\bf v}_{{{{\rm ref}}}}$ is the velocity in the free-flow region of the reference solution while $\Delta {\bf v}$ is the corresponding difference between the reference solution and the one of the coupled model. In analogy to Eq. (21), we determined $\eta _{\rm p} = \eta _{\rm p}^{{{\rm old}}} / \eta _{\rm p}^{{{\rm new}}}$ to evaluate the influence of Eq. (11) on pressure.

Figure 4 shows $\eta _{\rm v}$ (full markers) and $\eta _{\rm p}$ (empty markers) for all geometric setups over the ratio of Reynolds numbers within the channel and the pore throat $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}}$, based on the corresponding mean velocity and the hydraulic diameter of the structures. For the injection scenarios ($p_{{{\rm bottom}}} / p_{{{\rm in}}} \ge 1$), an increase of $p_{{{\rm bottom}}}$ leads to higher flow rates within the pore throat which in turn decreases $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}}$ as the pressure drop $p_{{{\rm in}}} - p_{{{\rm out}}}$ driving the main-channel flow is kept constant. For $p_{{{\rm bottom}}} / p_{{{\rm in}}} = 0.33$ (extraction), the lowest flow rate in the throat is obtained for $\varphi _{{{\rm az}}} = 0^{\circ }$ and $\theta _{{{\rm pol}}} = 60^{\circ }$ (red circle). Here, the flow coming from the channel and entering the throat is reversed and rotated by $150^{\circ }$.

Fig. 4

Error reduction for different configurations. The filled markers show the reduction of the velocity-related error $\eta _{\rm v}$ (Eq. 21) for different geometrical setups and flow configurations. The empty markers show the corresponding value $\eta _{\rm p}$ for the pressure

The error reduction provided by Eq. (11) strongly depends on $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}}$, while the orientation of the throat does not have a significant impact.

For $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} > 10$, ${{{\rm err}}}_{\rm v}$ is reduced by a factor of more than five for all cases considered, while ${{{\rm err}}}_{\rm p}$ is more than halved. For comparison, we also considered the case of $\varphi _{{{\rm az}}} = 0^{\circ }$ and $\theta _{{{\rm pol}}} = 0^{\circ }$ where the boundary of the lower pore body was closed such that no flow occurred in the throat. This corresponds to the simplified configuration used for the evaluation of $\beta _{{{{\rm pore}}}}$ in the previous section. Here, we obtained a benefit of $\eta _{\rm v} = 5.63$ and $\eta _{\rm p} = 2.44$ which shows that the simplifications made for the determination of $\beta _{{{{\rm pore}}}}$ do not impair the accuracy of the method for the given cases.

However, we observe a steep drop of $\eta _{\rm v}$ and $\eta _{\rm p}$ for $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} < 10$. In order to assess whether this is due to the above-mentioned simplifications, we re-evaluated $\beta _{{{{\rm pore}}}}$ for $\varphi _{{{\rm az}}} = 45^{\circ }, \theta _{{{\rm pol}}} = 0^{\circ }$ and $p_{{{\rm bottom}}} / p_{{{\rm in}}} = 100$ based on the results of the corresponding reference solution, taking into account the horizontal flow velocity within the pore throat such that

$$\begin{aligned} \beta _{{{\rm pore, new}}} \approx \frac{ \left\langle \left[ \frac{\partial v_x }{\partial y} + \frac{\partial v_y }{\partial x} \right] ^{{{\rm FF}}}\right\rangle }{\left\langle \left[ v_x \right] ^{{{\rm FF}}}\right\rangle - \left[ v_x \right] ^{{\rm PNM}}}. \end{aligned}$$

(23)

This yields a new value of $\beta _{{{{\rm pore}}}}= -21{,}541\,\hbox {m}^{-1}$. The negative sign is due to the fact that in this case, the velocity within the pore throat is actually higher than the free-flow velocity at the interface. Using this new value for the coupled model only slightly improves the results with $\eta _{\rm v} = 1.14$ and $\eta _{\rm p} = 1.17$ (compared to $\eta _{\rm v} = 1.08$ and $\eta _{\rm p} = 1.13$). The decrease of $\eta$ is therefore caused by something else, as shown in Fig. 5: for $p_{{{\rm bottom}}} / p_{{{\rm in}}} = 1$ (Fig. 5a), the flow directly above the coupling pore is mainly parallel to the free-flow channel’s x-axis. It is entirely governed by the pressure drop between the channel’s inlet and outlet which also results in a rather homogeneous pressure distribution along the coupling interface. In strong contrast to this, Fig. 5b shows the effect of the pronounced inflow coming from the pore throat when $p_{{{\rm bottom}}} / p_{{{\rm in}}} = 100$. This influx causes the velocity field to diverge due to the locally increased pressure on the left side of the coupling interface. The velocity field is therefore not governed by the free-flow channel’s bulk pressure gradient anymore but shaped by the local influx at the pore. This can also be quantified in terms of the standard deviation of the pressure field on the coupling interface $\Gamma _i$: for $p_{{{\rm bottom}}} / p_{{{\rm in}}} = \{0.33, 1, 10, 100\}$, the standard deviation is $1.09\times 10^{-7}\,\hbox {Pa},\, 1.09\times 10^{-7}\,\hbox {Pa},\, 1.13\times 10^{-7}\,\hbox {Pa}$ and $3\times 10^{-7}\,\hbox {Pa}$, respectively. It thus correlates inversely proportional with $\eta _{\rm v}$ and $\eta _{\rm p}$ (Fig. 4). The coupled model assumes a constant pressure on $\Gamma _i$ (Eq. 6) for the balance of normal forces. This assumption is obviously not met for high flow rates within the coupling throat. This issue is, however, not related to the slip condition proposed here. Furthermore, in many technical and environmental applications, the free-flow bulk velocity is likely to be considerably higher than the velocity within the pore throats at the interface, corresponding to $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} > 10$ where Eq. (11) performs well.

Fig. 5

Pressure field and velocity vectors of the reference solution at the coupling interface as seen from the top (x–z-plane) for $\varphi _{{{\rm az}}} = 45^{\circ }$, $\theta _{{{\rm pol}}} = 0^{\circ }$

In conclusion, the novel slip condition reduces the coupled model’s error with respect to the reference solution in the free-flow channel by a factor of over five for the velocity and by more than two for the pressure, provided that the ratio between the Reynolds numbers in the channel and in the throat $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} > 10$. The pore throat’s orientation does not have a significant effect. If the flow through the interface pore strongly affects the overall flow field, the coupled model’s accuracy is limited by the coupling condition for the normal momentum exchange, which assumes a uniform pressure at the pore. This could be addressed in future work.

The next section features a three-dimensional showcase where the coupled model is applied to a free-flow channel above a randomly generated pore network.

4 A Three-Dimensional Showcase with a Random Network

This example serves to illustrate the coupled model’s ability to handle unstructured pore networks in 3D while reducing the computational cost compared to a fully resolved reference solution. Figure 6 shows the setup which features a free-flow channel above a randomly generated network of pores which was created following the procedure described by Raoof and Hassanizadeh (2009). Starting from a regular lattice of $3 \times 3 \times 3$ pores ($\Delta x = \Delta y = \Delta z = 2\times 10^{-4}\,\hbox {m}$) where the nodes are connected to all neighbors, some connections are deleted randomly. The remaining connections are the pore throats with a uniform radius of $r_{ij} = 5\times 10^{-5}\,\hbox {m}$ while the nodes are the pore bodies with $r_i = 1\times 10^{-4}\,\hbox {m}$. We assured that throats only intersect at the pore bodies and that the coordination number of the latter at the interface is always one. The resulting network (shown in black in Fig. 6) features 42 throats and 26 pore bodies. A three-dimensional grid featuring 4,320,307 uniform cells (including 3,200,000 cells in the free-flow channel) was then constructed based on this network, as shown in gray in Fig. 6. As in the previous sections, we chose the grid resolution such that 40 cells per pore body diameter are used.

Fig. 6

3D geometry consisting of a free-flow channel and a random network. The opaque gray 3D reference geometry was created from the random 1D network shown in black

Flow is induced in the channel and in the network by setting $p_{{{\rm in}}} = 1\times 10^{-6}\,\hbox {Pa},\, p_{{{\rm out}}} = 0\,\hbox {Pa}$ and $p_{{{\rm bottom}}} = 1\times 10^{-6}\,\hbox {Pa}$. All remaining boundaries are set to no-flow/no-slip. Equation (20) and $\beta _{{{{\rm pore}}}}= 57 348\,\hbox {m}^{-1}$ are considered for the coupled model. Water with $\mu = 1\times 10^{-3}\,\hbox {Pa}\,\hbox {s}$ is used.

Solving the stationary Stokes equations (Eqs. 1, 2) with DuMu^x on a single core (Intel Xeon CPU E5-2683 v4 @ 2.10 GHz, 62 GB RAM) took $65\,\hbox {min}$ for the reference model and $47\,\hbox {min}$ for the coupled model, regardless of whether using Eq. (11) or Eq.  (7). The total CPU time including grid creation, matrix assembly and I/O was $82\,\hbox {min}$ for the reference model and $54\,\hbox {min}$ for the coupled model. The speedup of $\tfrac{65}{47} = 1.4$ with respect to solver time corresponds to the ratio of the number of degrees of freedom for the reference model and for the coupled model, $\tfrac{17{,}480{,}883}{12{,}872{,}026}= 1.36$, showing the almost linear scaling behavior of the iterative solver.

The coupled model’s results (Fig. 7b) match closely with the reference solution (Fig. 7a) in a qualitative sense. Some local deviations of up to $20\%$ with respect to ${\bf v}$ occur at pore bodies with pronounced inflow which corresponds to the discussion related to Fig. 5.

Fig. 7

Results for the random 3D network. The velocity (magnitude) directly above the coupling interface is shown by the plane in red and blue. The gray velocity vectors are scaled by magnitude. The one-dimensional network in (b) is extruded for visualization purposes

The coupled model’s normalized errors for the free-flow channel (Eq. 22) are ${{{\rm err}}}_{\rm v} = 4.78\times 10^{-3}$ and ${{{\rm err}}}_{\rm p} = 4.92\times 10^{-3}$ when considering Eq. (11), compared to ${{{\rm err}}}_{\rm v} = 2.84\times 10^{-2}$ and ${{{\rm err}}}_{\rm p} = 1.14\times 10^{-2}$ for Eq. (7). This yields (Eq. 21) $\eta _{\rm v} = 5.94$ and $\eta _{\rm p} = 2.32$ which is in the same range as in the previous section when $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} > 10$ (Fig. 4). For the given setup, $Re_{{{\rm bulk}}} = 5.85\times 10^{-6}$ (based on the channel’s hydraulic diameter and mean velocity) while $Re_{{{\rm throat}}} = 3.22\times 10^{-8}$ (evaluated using the throats adjacent to the interface pores with a uniform hydraulic diameter of $2 r_{ij}$ and the mean velocity within those throats).

Repeating all simulations with an increased bottom pressure of $p_{{{\rm bottom}}} = 1\times 10^{-5}\,\hbox {Pa}$ leads to $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} = 10.22$, yielding $\eta _{\rm v} = 3.18$ and $\eta _{\rm p} = 1.7$ which is again in accordance with our previous findings (Fig. 4).

In conclusion, this example showed that the coupled model can also be effectively applied to larger three-dimensional network structures where the benefit of using the proposed slip condition shows the same scaling behavior with $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}}$ as in our previous error analysis considering only a single throat. In the next and last section, we will recalculate a microfluidic experiment using the coupled model.

5 Recalculation of a Micromodel Experiment

In this section, we use the coupled model to recalculate a micromodel experiment of Terzis et al. (2019) where we exploit the quasi-two-dimensional nature of the experimental setup. The latter is especially suited for applying the proposed slip condition (Eq. 11) as it features only pore throats intersecting normally with the coupling interface which would result in a no-slip condition when using Eq. (7).

Fig. 8

Schematic of the micromodel used in the experiment (redrawn from Terzis et al. 2019) with dimensions, origin of coordinates and flow direction. The model has a height in z-direction of $200\,{\upmu}\hbox {m}$, the pillars are quadratic with $l = 240\,{\upmu}\hbox {m}$ and evenly spaced throughout the porous domain

The micromodel geometry is shown in Fig. 8. It features three main regions: (1) the free-flow channel at the top, (2) the porous medium made of $80 \times 20$ evenly spaced quadratic pillars and (3) a triangular reservoir region which was included into the design to facilitate the complete saturation of the model with water through an auxiliary inlet (not shown) at the bottom. This inlet was closed during the experiments. Details on the experimental procedure can be found in Terzis et al. (2019). For convenience, two dimensionless lengths x/l and y/l are introduced, where $l = 240\times 10^{-6}\,{\hbox {m}}$ is the width of the pores in the porous region. The model has a uniform height of $200\times 10^{-6}\,\hbox {m}$ in z-direction. Note that the inlet and outlet parts of the actual micromodel are longer to ensure a fully developed flow profile at the beginning of the porous medium during the experiment. For the simulations, these parts of the channel have been shortened (and correspond to the dimensions given in the drawing) for efficiency reasons while a fully developed flow was still achieved by applying pressure boundary conditions at the inlet and the outlet ($p_{{{\rm in}}} = 1\times 10^{-3}\,\hbox {Pa}$ and $p_{{{\rm out}}} = 0\,\hbox {Pa}$). All remaining walls were set to no-slip/no-flow. Again, water is used ($\mu = 1\times 10^{-3}\,\hbox {Pa}\,\hbox {s}$).

As in the previous sections, we first generate a three-dimensional reference solution for comparison with the coupled model. This is achieved, after ensuring grid convergence, by uniformly meshing the entire micromodel using more than 62 million regular, axis-parallel cells, such that each pore throat is discretized with 20 cells in all directions. Since the free-flow model of DuMu^x is not parallelized yet, we use the open-source CFD tool OpenFOAM (Jasak 2009) for obtaining the stationary flow field in this case for sake of efficiency. A close match between the reference solution and the experimental data of Terzis et al. (2019) is found, as shown in Appendix 1.

For the coupled model, we simplify the micromodel geometry by reducing it to a two-dimensional plane where the z-coordinate and all velocities in this direction are omitted. Assuming a parabolic flow profile along the z-axis, Flekkøy et al. (1995) proposed a drag term which accounts for the wall friction of the virtual frontal and rearward boundary:

$$\begin{aligned} {\bf f}_{{{\rm drag}}} = - c \frac{\mu }{{h}^2} {\bf v}. \end{aligned}$$

(24)

${h}$ is the virtual height of the model domain while c is a constant which determines whether the maximum velocity at the central plane of the channel at $0.5{h}$ ($c = 8$) or the height-averaged one ($c = 12$) is recovered. This approach has been applied successfully for a number of different applications with Hele-Shaw-type flow (Venturoli and Boek 2006; Laleian et al. 2015; Kunz et al. 2015; Class et al. 2020) and provides the best accuracy for ${h}\ll w$ where w is the width of the flow channel. Equation (24) is added as a momentum source term to the left side of Eq. (1).

We chose a factor of $c = 8$ to obtain the maximum, center-plane velocities because this corresponds to the experimental micro-PIV data and a comparison with the 3D OpenFOAM results is straightforward since we just need to extract the center plane from the 3D simulation data rather than performing an averaging along the z-axis. Note that the coupling between the free-flow domain and the pore-network model is still realized in terms of volumetric flow rates which can be approximated from the quasi-3D model by

$$\begin{aligned} Q_{{{\text{quasi-3D}}}} = \tfrac{2}{3} {h}\int _s ({\bf {\bf v}} \cdot {\bf n}) {{{\rm d}}} s. \end{aligned}$$

(25)

${\bf n}$ is a unit vector normal to the line s over which the flow is evaluated, extruded in the virtual z-direction by the domain’s height ${h}$. The factor 2/3 transfers the maximum velocity to a height-averaged one, assuming again a parabolic profile along the omitted z-axis.

In the following, the results of four different models will be discussed: the center-plane data ($z= 100\times 10^{-6}\,\hbox {m}$) of the three-dimensional reference model (OpenFOAM), the results of the quasi-3D model applied to the entire micromodel (DuMu^x) and those of the coupled model using either Eq. (7) or Eq. (11) (DuMu^x). The coupled model treats the free-flow channel and the triangular region with the Stokes equations (Eqs. 1, 2) while the porous domain is accounted for by the pore-network model. We used the quasi-3D model to determine the input parameter $\beta _{{{{\rm pore}}}}= 30{,}983\,\hbox {m}^{-1}$ as described in Sect. 3. Interestingly, introducing the wall friction term ${\bf f}_{{{\rm drag}}}$ leads to a nonlinear scaling of $\beta _{{{{\rm pore}}}}$ over $r_i$. Further investigation of this behavior is required in future work. The throat conductance including the pressure loss within the pore bodies,

$$\begin{aligned} g_{ij} = \left( g_{ij,t}^{-1} + g_{1/2, i}^{-1} + g_{1/2, j}^{-1} \right) ^{-1}, \end{aligned}$$

(26)

with $g_{ij,t} = 3.05\times 10^{-10}\,\hbox {m}^{3}/(\hbox {Pa s})$ and $g_{1/2, i} = g_{1/2, j} = 8.47\times 10^{-10}\,\hbox {m}^{3}/(\hbox {Pa s})$, was determined using again the quasi-3D model and the numerical upscaling approach described in the appendix of Weishaupt et al. (2019).

In contrast to the previous numerical examples, we employ the direct linear solver UMFPack (multifrontal LU factorization, Davis 2004) to solve the linear system of equations in DuMu^x. This is feasible and actually more efficient than using the iterative approach described in Sect. 2.4 due to the system’s moderate size with 9,412,010 and 3,737,351 degrees of freedom for the quasi-3D model and the coupled one, respectively. The corresponding CPU times were 11 min and 5 min on a single core of the same machine as before.

Fig. 9

Velocity and pressure fields for the micromodel setup. The center-plane ($z= 100\times 10^{-6}\,\hbox {m}$) velocity (magnitude) and pressure fields of the 3D reference solution obtained with OpenFOAM are shown in (a) and (b). The corresponding results of the coupled model using the novel slip condition are given in (c) and (d) where the one-dimensional elements of the pore network have been extruded for visualization purposes. Note that the pore throats in the coupled model show averaged velocities based on Eq. (4) which are by implication smaller than the peak free-flow velocities at the associated interface

Figure 9 shows the center-plane velocity and pressure fields of the reference and the coupled model using Eq. (11). As observed in the experiment (Terzis et al. 2019, cf. Appendix 1), the flow enters the porous domain almost vertically on the left side of the porous medium, traverses it mainly parallel and re-enters the channel on the right side of the porous domain. A substantial fraction of flow passes through the triangular reservoir at the bottom of the model as this features less resistance than the narrow flow channels within the porous medium. The maximum resulting Reynolds number, both with respect to the free-flow channel and the one of the pore throats (considering the hydraulic diameter), is always below $1\times 10^{-3}$.

There is a high level of visual agreement between the reference and the coupled solution. Local velocity deviations in the free-flow channel of up to $4\%$ can be observed, especially on the leftmost and rightmost vertical throat intersecting with the interface. This is probably due the velocity gradients which are highest at these positions and the sudden change of flow direction. In addition, the aspect ratio between the model height ${h}$ and the flow cross-section changes from a value of 0.1 ($\frac{200\,{\upmu }{\rm m}}{2000\,{\upmu }{\rm m}}$) in the channel to a less favorable value of 0.83 ($\frac{200\,{\upmu }{\rm m}}{240\,{\upmu }{\rm m}}$) in the pore throats, which impairs the validity of Eq. (24).

The volumetric flow rates for each throat at the interface are given in Fig. 10. The throats are labeled from left to right from #1 to #81. The in- and outflow behavior across the interface is symmetrical and, as expected, no flow occurs at the horizontal center of the micromodel (#40). The coupled models’ results are almost identical to the ones of reference solution, regardless of whether Eq. (7) or Eq. (11) is used which means that the vertical mass exchange between the free flow and porous medium is not significantly influenced by the slip velocity above the throats.

Fig. 10

Pore-local volume fluxes. Discrete volumetric flow rates at all throats intersecting with the interface for all numerical models, normalized by the maximum flow rate of the 3D reference model (OpenFOAM). “new” refers Eq. (11), “old” to Eq. (7)

In Fig. 11, the central throat # 40 intersecting with the interface at $y/l = 0, x/l = 80.5$ is magnified and the velocity vectors of the 3D reference, the quasi-3D and the coupled models are shown. The main channel flow slightly dips into the throat cavity on the left just to re-enter the main channel on the right. There is no net mass flux across the interface. This flow behavior is generally reflected by all models. Using Eq. (11) instead of Eq. (7) in the coupled model noticeably improves the agreement with the reference solution’s vectors, both in magnitude and orientation.

The vertical velocity component of both coupled models is essentially determined by the coupling condition for the conservation of momentum in normal direction (Eq. 6) and is thus more or less identical corresponding to our previous findings in Fig. 10. The black vectors feature strongly decreased x-components due to the no-slip condition at the coupling interface yielded by Eq. (7) for this type of geometry.

Fig. 11

Near-interface flow field. Close-up of the interface region at the central throat ($x/l= 80.5, y/l = 0$). The yellow, purple and black velocity vectors correspond to the quasi-3D model, the coupled model considering Eq. (11) and the coupled model considering Eq. (7). The opaque white vectors with contours (barely visible as they mostly overlap with the quasi-3D vectors) correspond to the 3D center-plane ($z= 100\times 10^{-6}\,\hbox {m}$) results of OpenFOAM

The same pattern can be observed in Fig. 12 which shows a close-up of the two leftmost throats at the interface. Here, we see a pronounced downward flow from the free-flow channel into the porous domain. Again there is a much better match with the reference solution if the slip velocity is taken into account using Eq. (11).

Fig. 12

Near-interface flow field. Close-up of the interface region at the two leftmost throats ($0 \le x/l \le 3, y/l = 0$). The yellow, purple and black velocity vectors correspond to the reference (quasi-3D) model, the coupled model considering Eq. (11) and the coupled model considering Eq. (7). The opaque white vectors with contours (barely visible as they mostly overlap with the quasi-3D vectors) correspond to the 3D center-plane ($z= 100\times 10^{-6}\,\hbox {m}$) results of OpenFOAM

Table 3 summarizes the normalized errors for the free-flow channel and the triangular region of micromodel setup. In the first row, the 3D center-plane results (OpenFOAM) serve as reference solution. As seen in the last column, the largest portion of the error originates from the quasi-3D simplification (here the quasi-3D free-flow model is applied to the entire geometry).

As explained above, the coupled model employs the quasi-3D model in the free-flow channel and in the triangular region and the relevant input parameters $\beta _{{{{\rm pore}}}}$ and $g_{ij}$ have been determined using the quasi-3D model. For sake of comparability, we therefore consider the latter (applied to the whole geometry) as a reference for the coupled models in the second row of Table 3 and obtain a benefit for using the novel slip condition (Eq. 21) of $\eta _{\rm v} = 2.52$ and $\eta _{\rm p} = 1.25$. For the entire free-flow channel, $Re_{{{{\rm bulk}}}} / Re_{{{{\rm throat}}}} = 12.25$ ($Re_{{{{\rm throat}}}}$ based on the mean velocity of the throats at the interface and their hydraulic diameter) for which we would expect slightly higher values of $\eta$ according to Fig. 4. However, the flow across the interface is not uniform (see Fig. 10) and $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} = 1.87$ for the leftmost and rightmost throat, for which even lower values of $\eta$ were found in Fig. 4. The smaller an interfacial throat’s distance from the center $x/l = 80.5$, the lower $Re_{{{\rm throat}}}$ and the more favorable the conditions for applying Eq. (11) which explains the results for $\eta$ ranging in-between the bounds presented in Fig. 4.

Table 3 Normalized errors for the free-flow channel and the triangular region of micromodel setup

Finally, Fig. 13 sheds some light onto the horizontal flow conditions within the free-flow channel, the porous medium and the triangular region at the vertical center line of the micromodel. Depicted are the normalized horizontal velocities at $x/l = 80.5$ and the integral volume flows Q at the throats directly left to the center line at $x/l = 79.5$, likewise normalized. As the pore-network model only yields averaged velocities within the pore throats, $v_x$ is only drawn in the free-flow channel and the triangular region, where it matches almost perfectly the solution of the quasi-3D model. Both coupled models and the quasi-3D one also give rise to very similar integral volume flows within the throats, which deviate by around 6% from the values of the 3D simulation. This can be explained by the aforementioned unfavorable aspect ratio of 0.83 in the pore throats which impairs the accuracy of Eq. (24) used for the quasi-3D model from which subsequently also the throat conductances were derived by numerical upscaling, as described previously. The inset image on the lower left of Fig. 13 shows, as expected, a higher value of $v_x$ right at the interface when Eq. (11) is used in the coupled model.

Fig. 13

Horizontal velocity profiles and volumetric fluxes over height. Velocity profiles $v_x$ over y at $x/l = 80.5$ and discrete volumetric flow rates at $x/l = 79.5$ for all numerical models, normalized by the maximum values of the 3D reference model (OpenFOAM). The coupled model only features continuous velocities in the free-flow channel and the triangular region. “new” refers Eq. (11), “old” to Eq. (7)

In summary, this section showed how the coupled model can be applied to recalculate a microfluidic experiment. We considered the results of a fully resolved 3D simulation and the one of a simplified quasi-3D model for comparison with the coupled model. The latter also made use of the quasi-3D approach in the free-flow regions. The coupled model was more than twice as fast as the quasi-3D model applied to the entire domain while providing a high degree of accuracy, especially when making use of Eq. (11).

6 Conclusion

In this work, we have extended and improved the hybrid-dimensional coupled model of Weishaupt et al. (2019) where only two-dimensional setups were considered and the coupling conditions for tangential momentum transfer would effectively yield no-slip conditions for throats oriented orthogonally with the coupling interface. Here, we introduced a novel condition for pore-scale slip and considered three-dimensional computational domains. The accuracy of this condition was assessed in detail on the example of a single pore intersecting with a free-flow domain under various geometrical settings and flow conditions. The slip condition can reduce the normalized error within the free-flow domain by a factor of more than five, provided the flow through the intersecting pore does not substantially influence the free-flow velocity field, i.e, $Re_{{{\rm bulk}}} / Re_{{{\rm throat}}} > 10$. These findings also hold when the coupled model is applied to a complex, three-dimensional random network coupled to a free-flow channel. Weishaupt et al. (2019) used a direct linear solver due to the poorly conditioned monolithic system matrix. We lifted this constraint here be applying an iterative linear solver in combination with a simple preconditioning strategy based on the Uzawa algorithm (Ho et al. 2017). Following the first promising results obtained here, we will investigate further ways to improve the linear solver, such as proposed by Kuchta et al. (2018), while also aiming for parallelization. In addition, alternatives to our monolithic coupling scheme will be investigated (Bungartz et al. 2016; Jaust et al. 2020). The limitation to free-flow grids conforming with the discrete pore bodies at the coupling interface could be addressed in future work by considering mortar techniques (Song et al. 2013; Mehmani and Balhoff 2014).

In the last section of this work, we applied the coupled model for the recalculation of a microfluidic experiment (Terzis et al. 2019). Here, the coupled model’s results were in high accordance with the numerical reference solution and the proposed slip condition again proved beneficial.

In summary, the coupled, hybrid-dimensional model is an interesting and efficient option for the simulation of coupled systems of free flow over a permeable medium. It can be certainly used as a powerful design tool during the optimization of microfluidic experiments as well as in industrial applications providing accurate results in a timely manner.

Appendix 1: Comparison of 3D Simulation Results with Micro-PIV Experimental Data

Figure 14 is a reproduction of Fig. 7a presented in Terzis et al. (2019), using the same experimental data and color scheme. In Fig. 14c, the results of the micro-PIV measurements are shown in terms of $v_y$ and the velocity vector fields for four different locations A, B, C and D, as indicated in Fig. 14a. Figure 14b displays the corresponding simulation results (OpenFOAM) which show a very good agreement with the experimental data in a qualitative sense, reproducing the same distinct flow patterns at the various locations: in region A, a pronounced inflow from the free-flow channel into the porous structure can be observed which diminishes in streamwise direction. Region C basically shows a mirrored flow field as the fluid leaves the porous medium and re-enters the channel symmetrically compared to A. Here, the vertical flow intensity increases again in streamwise direction. In region B, at the center of the porous domain, no net influx or outflux occurs. The fluid crosses the interface in a downwards motion on the right sides of the solid blocks (red spots) and returns to the free flow channel at left sides of the blocks (blue spots). Region D lies inside the porous domain and features mainly parallel flow in x-direction.

Fig. 14

Comparison of flow fields obtained by numerical simulation with OpenFOAM (b) and micro-PIV measurement results (c, reproduced from the original data of Terzis et al. 2019). The regions A, B, C and D are shown in (a)

In Fig. 15a, a more quantitative comparison is performed. Here, $v_x$ is averaged in x-direction between $75 \le x/l \le 85$ along a vertical column, as shown by area E in Fig. 15b. Both the experimental and numerical data are given and the graphs are normalized by the respective maximum values in the free-flow region. A very good fit can be found, both qualitatively and quantitatively. The local deviations can be explained by measurements uncertainties (Terzis et al. 2019) or small-scale structural differences between the actual micromodel geometry and the computational domain, such as surface roughness (Silva et al. 2008) which is not captured by the numerical model. While Fig. 15c shows that the pillars of the micromodel are indeed not entirely smooth and that the corners are slightly rounded, the numerical model only considers perfectly smooth squares with sharp corners. This could also explain the local deviations of flow angles $\vartheta$ close to the interface between the free-flow channel and porous medium, as presented in Fig. 16. A detailed analysis of the impact of the pillars’ rounded edges is beyond the scope of this work and should be addressed in future studies.

Fig. 15

Experimental and numerical velocity profiles. a Comparison of averaged velocity profiles ($75 \le x/l \le 85$) between simulation (OpenFOAM) and experiment. The original data of Terzis et al. (2019) were used. $v_x$ is averaged in x-direction between $75 \le x/l \le 85$ at different locations of y, see area E in (b). c Camera image of a pillar within the porous domain showing the surface roughness of the pillar as a potential source of error

Figure 16 shows a symmetric characteristic of the flow angles due to the inflow into the porous medium and the outflow back into the free flow channel. On the left, the velocity vectors feature a negative inclination as the flow enters the porous domain while the same angles with opposed sign can be found on the right side, where the flow returns to the free flow channel. The local oscillations are caused by the same up- and downwards movement of the flow between the pillars as explained for region B in Fig. 14. The angles are greater for $y/l = 0.1$, which is closer to the interface, as the free flow in channel senses a stronger influence of the porous medium compared to $y/l = 0.5$.

In summary, the three-dimensional numerical model is able to reproduce the experimental data adequately. The obtained reference solution is thus suited for comparison with the reduced model’s results as described in Sect. 5.

Fig. 16

Experimental and numerical flow angles. Comparison of the flow angles $\vartheta$ close to the interface between free flow and porous medium at $y/l=0.5$ (a) and $y/l=0.1$ (b) for the simulation and the experiment. The original data of Terzis et al. (2019) were used