1 Introduction

Nield and Kuznetsov (2016) produced an inspiring article in which they address the behaviour of the onset of convective motion in a layer of porous material which is saturated by a fluid containing a dissolved salt. They consider both Brinkman and Darcy theory, and they are primarily interested in the case where the heat flux and salt flux are prescribed on the boundary. They do, however, also consider the case where general thermal and salt boundary conditions are employed which involve a combination of flux and prescribed temperature and salt. They develop an asymptotic and a numerical analysis to study how oscillatory convection behaves as boundary conditions of flux only are considered. It is well known that in the heated below–salted below situation there is a transition from stationary convection to oscillatory convection as the salt Rayleigh number increases. The current article is motivated entirely by the work of Nield and Kuznetsov (2016), and we analyse how the transition from stationary to oscillatory convection is affected as the boundary conditions change.

Double diffusive convection is a problem with many real-life applications and as such has attracted much attention in the research literature, see, e.g. Barletta and Nield (2011), Deepika (2018), Deepika and Narayana (2016), Harfash and Challoob (2018), Harfash and Hill (2014), Joseph (1970), Joseph (1976), Lombardo et al. (2001), Matta et al. (2017), Mulone (1994), Nield (1967, 1968), Nield and Kuznetsov (2016), Straughan (2011, 2014, 2015a, 2018, 2019) and Xu and Li (2019). Stability analyses in double diffusive convection were introduced in the fundamental articles of Nield (1967, 1968), and from an unconditional energy stability point of view by Joseph (1970, 1976). Research activity in this area has increased rapidly as is witnessed by the articles cited above and the references therein.

Another very interesting development in stability in thermal convection studies has been to consider boundary conditions which are more general than those of prescribing temperature and salt concentration. For example, isoflux conditions, isobaric conditions, or various combinations. In many cases, these boundary conditions lead to surprising and novel results, see, e.g. Barletta (2012), Barletta et al. (2010), Barletta and Rees (2012), Barletta and Celli (2018), Celli and Barletta (2019), Celli et al. (2016), Celli et al. (2013), Celli and Kuznetsov (2018), Falsaperla et al. (2010, 2011), Lagziri and Bezzazi (2019), McKibbin (1986), Mohammad and Rees (2017), Nield and Kuznetsov (2016), Rees and Barletta (2011), Rees and Mojtabi (2011), Rees and Mojtabi (2013), Salt (1988) and Webber (2006).

Given the interest in double diffusive convection, especially where the salt and temperature effects are in competition as in the heated and salted below case, and the attention to general boundary conditions where a combination of flux and prescribed temperature/salt is studied, we believe this work is noteworthy. We also corroborate some of the findings of Nield and Kuznetsov (2016) as boundary conditions of pure flux are approached.

2 Equations

The derivation of the equations for double diffusion in a porous layer is well known. We present the non-dimensional perturbation equations in terms of the velocity, pressure, temperature and concentration perturbations, \(u_i,\pi ,\theta \) and \(\phi \), cf. Nield and Kuznetsov (2016), Mulone (1994) and Straughan (2014), Eq. (5),

$$\begin{aligned} \begin{aligned}&0=u_i+R\theta k_i-C\phi k_i-\pi _{,i},\\&u_{i,i}=0,\\&\theta _{,t}+u_i\theta _{,i}=w+\Delta \theta ,\\&\epsilon _1\phi _{,t}+Le u_i\phi _{,i}=w+\Delta \phi \end{aligned} \end{aligned}$$
(1)

where R and C are the Rayleigh and salt Rayleigh numbers, \(\mathbf{k}=(0,0,1)\), \(\epsilon _1=\epsilon Le\), where \(\epsilon \) is the porosity and Le is the Lewis number, \(\Delta \) is the Laplace operator, and standard indicial notation is employed. Equation (1) holds in the layer \(\{(x,y)\in \mathbb {R}^2\}\times \{z\in (0,1)\}\) with \(t>0\).

The boundary conditions may be derived as in Nield and Kuznetsov (2016), where the temperature and concentration are specified on the boundaries \(z=0,1\) and the perturbations are subject to more general boundary conditions. Alternatively, in the dimensional variables, we may propose the temperature satisfies the boundary conditions

$$\begin{aligned} \begin{aligned}&\alpha \Bigl (\frac{\partial T}{\partial z}+\beta \Bigr )d+(1-\alpha )(T_L-T)=0,\qquad z=0,\\&\alpha \Bigl (\frac{\partial T}{\partial z}+\beta \Bigr )d+(1-\alpha )(T-T_U)=0,\qquad z=d, \end{aligned} \end{aligned}$$
(2)

where d is the layer depth, \(T_L\) and \(T_U\) are constants with \(T_L>T_U\), \(\beta =(T_L-T_U)/d\) and \(\alpha \) is a constant with \(0\le \alpha < 1\). Note that \(\alpha =0\) corresponds to prescribed upper and lower temperatures \(T_U\) and \(T_L\), whereas \(\alpha =1\) corresponds to flux boundary conditions. Equation (2) is usually known as Robin boundary conditions, and they allow a steady solution

$$\begin{aligned} {\bar{T}}=T_L-\beta z \end{aligned}$$

and then lead to the non-dimensional perturbation boundary conditions

$$\begin{aligned} \begin{aligned}&\alpha \theta _z-(1-\alpha )\theta =0,\qquad z=0,\\&\alpha \theta _z+(1-\alpha )\theta =0,\qquad z=1, \end{aligned} \end{aligned}$$
(3)

where \(\theta \) is the non-dimensional temperature perturbation. We introduce the parameter \(L=(1-\alpha )/\alpha \) (the Biot number) and note that (3) may be rewritten as

$$\begin{aligned} \begin{aligned}&\theta _z-L\theta =0,\qquad z=0,\\&\theta _z+L\theta =0,\qquad z=1. \end{aligned} \end{aligned}$$
(4)

A similar derivation involving the concentration C leads to non-dimensional perturbation boundary conditions on \(\phi \) as

$$\begin{aligned} \begin{aligned}&\phi _z-L\phi =0,\qquad z=0,\\&\phi _z+L\phi =0,\qquad z=1. \end{aligned} \end{aligned}$$
(5)

We here restrict attention to the case where L has the same value in (4) and (5). One could consider a general case where four different L values, \(L_i,\)\(i=1,\ldots ,4,\) are considered in (4) and (5).

We are interested in determining the threshold of instability and so we remove the nonlinear terms from (1) and then seek a solution like \(u_i=u_i(\mathbf{x})\,e^{\sigma t}\), \(\pi =\pi (\mathbf{x})\,e^{\sigma t}, \theta =\theta (\mathbf{x})\,e^{\sigma t}\), \(\phi =\phi (\mathbf{x})\,e^{\sigma t}\). We next remove the pressure by taking curlcurl of (1)\(_1\) and retain the third component of the resulting equation. Writing \(\mathbf{u}=(u,v,w)\), this leaves the system of equations

$$\begin{aligned} \begin{aligned}&0=\Delta w-R\Delta ^*\theta +C\Delta ^*\phi ,\\&\sigma \theta =w+\Delta \theta ,\\&\sigma \epsilon _1\phi =w+\Delta \phi , \end{aligned} \end{aligned}$$
(6)

where \(\Delta ^*=\partial ^2/\partial x^2+\partial ^2/\partial y^2\). This system is to be solved subject to boundary conditions (4), (5), together with

$$\begin{aligned} w=0,\qquad z=0,1, \end{aligned}$$
(7)

and the assumption that \(w,\theta ,\phi \) satisfy a periodic plane tiling planform in (x, y) (Chandrasekhar 1981, pp. 43–52).

The plane tiling planform h(x, y) is discussed at length in cf. Chandrasekhar (1981), pp. 43–52, and satisfies \(\Delta ^*h=-a^2h\), where a is a wavenumber. This allows one to decompose \(w,\theta ,\phi \) in terms of functions of form \(w=W(z)h(x,y)\), \(\theta =\Theta (z)h(x,y)\) and \(\phi =\Phi (z)h(x,y)\). Upon using these forms, one has to solve the eigenvalue problem

$$\begin{aligned} \begin{aligned}&(D^2-a^2)W+Ra^2\Theta -Ca^2\Phi =0,\\&(D^2-a^2)\Theta +W=\sigma \Theta ,\\&(D^2-a^2)\Phi +W=\epsilon _1\sigma \Phi , \end{aligned} \end{aligned}$$
(8)

and the boundary conditions

$$\begin{aligned} \begin{aligned}&W=0,\quad z=0,1,\\&\Theta _z-L\Theta =0,\quad z=0;\qquad \Theta _z+L\Theta =0,\quad z=1,\\&\Phi _z-L\Phi =0,\quad z=0;\qquad \Phi _z+L\Phi =0,\quad z=1. \end{aligned} \end{aligned}$$
(9)

Numerical solutions of (8) and (9) are presented in Sect. 5.

3 Exact Theory

Before discussing numerical results for various values of L, we recollect results when \(L=\infty \), i.e. when \(\alpha =0\). In this case, Eqs. (8) and (9) may be solved exactly and one finds the lowest two eigenvalues lead to the stationary convection threshold

$$\begin{aligned} R=C+4\pi ^2, \end{aligned}$$
(10)

and the oscillatory convection threshold

$$\begin{aligned} R=\frac{C}{\epsilon _1}+4\pi ^2\Bigl (\frac{1+\epsilon _1}{\epsilon _1}\Bigr ), \end{aligned}$$
(11)

with the oscillatory part of the eigenvalue satisfying

$$\begin{aligned} \sigma _i^2=\frac{\pi ^2}{\epsilon _1}(4\pi ^2+C-R). \end{aligned}$$
(12)

One may observe that curves (10) and (11) intersect at \((R^*,C^*)\) when \(\epsilon _1>1\), as is nearly always the case in real life, where

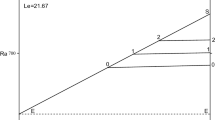
$$\begin{aligned} R^*=4\pi ^2\Bigl (\frac{\epsilon _1}{\epsilon _1-1}\Bigr ),\quad C^*=\frac{4\pi ^2}{(\epsilon _1-1)}. \end{aligned}$$

The behaviour of the (R, C) curves is shown in Fig. 1 when \(\epsilon _1=\epsilon Le=20\). In this case, the stationary convection curve has slope 1, while the oscillatory convection curve has slope 1/20. For \(C\le C^*\), one finds stationary convection, whereas for \(C>C^*\) oscillatory convection occurs.

Fig. 1
figure 1

Graph of R, C when the parameter L has infinite value (prescribed temperatures). Here, \(\epsilon Le=20\). The left branch of the solid curve is the stationary convection boundary, and the part after \((R^*,C^*)=(4\pi ^2(\epsilon Le/\epsilon Le -1),4\pi ^2/(\epsilon Le -1)),\) represents the oscillatory convection boundary. The broken line is a continuation of the stationary convection boundary

Full size image

If one employs purely flux boundary conditions, it is known that \(a=0\) yields the stationary convection boundary and then I calculate a weakly nonlinear analysis to show

$$\begin{aligned} R=C+12+\frac{34}{35}a^2+O(a^4), \end{aligned}$$

is the instability threshold. This suggests that \(R^*\in [12,4\pi ^2\epsilon _1/(\epsilon _1-1)]\) and \(C^*\in [12/\epsilon _1,4\pi ^2/(\epsilon _1-1)]\), for general values of L in (0,1]. Numerical analysis confirms this, and the behaviour is reported in Sect. 5.

Table 1 Values of \(R^*\) and \(C^*\) together with the critical value of a, namely, \(a_{\mathrm{cr}}\), and L
Full size table
Fig. 2
figure 2

Graph of R, C when the parameter L varies. Here, \(\epsilon Le=20\). The curves decrease in R as L decreases and are for \(L=\infty \) (uppermost curve), 10, 5, 2.5, 1, 0.1, 0.01 and \(10^{-4}\) (lowest curve). The dark solid circles represent \((R^*,C^*)\). The dotted lines represent the curves \(C=1,1.7,2.1,\) cf. Tables 2, 3 and 4

Full size image
Fig. 3
figure 3

Graph of \(R^*,C^*\). The parameter L varies from \(10^{-10}\) to \(\infty \). Here, \(\epsilon Le=20\). The values of L represented by the circles are \(10^{-10},10^{-8},10^{-6},10^{-4}\) shown as the four nearly coalesced circles on the lower left of the line (indistinguishable at this scale), and 0.01, 0.1, 1, 2.5, 5, 10, 100 and \(\infty \), with the last value being the circle on the upper right of the line. The dashed line for \(C^*\) between 0 and 2.5 represents the convection threshold \(R=12\)

Full size image
Table 2 Values of L and \(\sigma _i\) representing the values of \(\sigma _i\) on the critical oscillatory convection curve when \(C=2.1\)
Full size table
Table 3 Values of L and \(\sigma _i\) representing the values of \(\sigma _i\) on the critical oscillatory convection curve when \(C=1.7\)
Full size table
Table 4 Values of L and \(\sigma _i\) representing the values of \(\sigma _i\) on the critical oscillatory convection curve when \(C=1\)
Full size table

4 Numerical Methods

The numerical methods we employ are based on the Chebyshev tau method, see, e.g. Dongarra et al. (1996) and Gheorghiu (2014), and the resulting finite dimensional generalized matrix eigenvalue problem is solved with the QZ algorithm of Moler and Stewart (1971). Explicit details of this are given in Dongarra et al. (1996), and we write

$$\begin{aligned} W=\sum _{n=0}^NW_nT_n(z),\quad \Theta =\sum _{n=0}^N\Theta _nT_n(z),\quad \Phi =\sum _{n=0}^N\Phi _nT_n(z),\quad \end{aligned}$$

where \(T_n\) are the Chebyshev polynomials of the first kind and \(W_n,\Theta _n,\Phi _n\) are the Fourier coefficients. In terms of the vector

$$\begin{aligned} \mathbf{X}=(W_0,\ldots ,W_N,\Theta _0,\ldots ,\Theta _N,\Phi _0,\ldots ,\Phi _N), \end{aligned}$$

this leads to the matrix eigenvalue problem

$$\begin{aligned} A\mathbf{X}=\sigma B\mathbf{X} \end{aligned}$$

where

$$\begin{aligned} A= \begin{pmatrix} D^2-a^2I &{}\quad Ra^2I &{}\quad -Ca^2I\\ I &{}\quad D^2-a^2I &{}\quad 0\\ I &{}\quad 0 &{}\quad D^2-a^2I \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} B= \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad I &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \epsilon _1I \end{pmatrix} \end{aligned}$$
Table 5 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=100\)
Full size table
Table 6 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=10\)
Full size table
Table 7 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=5\)
Full size table
Table 8 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=2.5\)
Full size table
Table 9 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=1\)
Full size table
Table 10 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=0.1\)
Full size table
Table 11 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=0.01\)
Full size table
Table 12 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=10^{-4}\)
Full size table
Table 13 Values of \(a_{\mathrm{{cr}}},R,C\) and \(\sigma _i\) at criticality \(L=10^{-6}\)
Full size table
Fig. 4
figure 4

Graph of \(\log _{10}a,\log _{10}L\). Here, \(\epsilon _1=\epsilon Le=20\)

Full size image

Care must be taken with the boundary conditions to avoid the presence of spurious eigenvalues. Details of how one handles the boundary conditions \(W=0\) are given in Dongarra et al. (1996). To deal with the boundary conditions on \(\Theta \) and \(\Phi \), we note that \(T_n(\pm 1)=(\pm 1)^n\) and \(T_n^{\prime }(\pm 1)=(\pm 1)^{n-1}n^2\). One has to recollect that the Chebyshev domain is \((-1,1)\), and then one finds that the boundary conditions yield the restrictions

$$\begin{aligned}&2\left[ 2^2\Theta _2+4^2\Theta _4+\cdots +(N-3)^2\Theta _{N-3}+(N-1)^2\Theta _{N-1}\right] \\&\quad +L\left[ \Theta _0+\Theta _2+\cdots +\Theta _{N-3}+\Theta _{N-1}\right] =0 \end{aligned}$$

and

$$\begin{aligned}&2\left[ \Theta _1+3^2\Theta _3+\cdots +(N-2)^2\Theta _{N-2}+N^2\Theta _N\right] \\&\quad +L\left[ \Theta _1+\Theta _3+\cdots +\Theta _{N-2}+\Theta _N\right] =0. \end{aligned}$$

This allows one to write

$$\begin{aligned} \Theta _{N-1}&=-\frac{1}{[2(N-1)^2+L]}\,[(2\times 0^2+L)\Theta _0+(2\times 2^2+L)\Theta _2+\\&\quad \, \cdots +\{2(N-3)^2+L\}\Theta _{N-1}] \end{aligned}$$

and

$$\begin{aligned} \Theta _N&=-\frac{1}{[2N^2+L]}\,[(2\times 1^2+L)\Theta _1+(2\times 3^2+L)\Theta _3+\\&\quad \, \cdots +\{2(N-2)^2+L\}\Theta _{N-2}] \end{aligned}$$

Analogous expressions hold for \(\Phi _{N-1}\) and \(\Phi _N\). These expressions are used to remove boundary condition rows, cf. Dongarra et al. (1996), in the matrices A and B and are very important in dealing with spurious eigenvalues.

To find \((R^*,C^*)\) numerically is not trivial. We used two codes. One tracks along the stationary convection curve from \(C=0\) and then tracks along the oscillatory convection curve in the opposite direction. When we are in the vicinity of \((R^*,C^*)\), the two leading eigenvalues \(\sigma _1\) and \(\sigma _2\) one of which is real, whereas the other is complex, have real parts close to zero and close to each other; therefore, the code switches from one to the other and breaks down. Thus, we extrapolate from the stationary and oscillatory convection curves for a given value of L to find an approximate value for \(R^*\) and \(C^*\). We then employ a second code which compares \(\sigma _1\) and \(\sigma _2\) in the vicinity of the “crossing point” and varies over a suitable range of wavenumber a. In this way, we actually find where \(\sigma _1\) and \(\sigma _2\) swap places, to 3 decimal places of accuracy in R. Numerical results employing these procedures are presented next.

5 Numerical Results and Conclusions

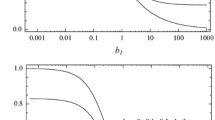
The values of \(R^*\) and \(C^*\) as L varies are displayed in Table 1 and in Figs. 2 and 3. From Fig. 3, it appears that \((R^*,C^*)\) form approximately a straight line with L varying. The critical values of a are in agreement with the values in table 1 of Nield and Kuznetsov (2016), who give values of R and \(a_{\mathrm{cr}}\) as L varies for the problem of thermal convection (without a solute). We found \(R^*\in (12.631,12.632)\) and \(C^*\in (0.6315,0.6316)\) when \(L=10^{-10}\), and we found a similar value for \(C^*\) when \(L=10^{-12}\).

The critical wavenumber \(a_{\mathrm{{cr}}}\) varies with L, but we found no variation with C, as seen in Tables 5, 6, 7, 8, 9, 10, 11, 12 and 13. For \(L\le 0.1\), we found the graph of \(\log _{10}a\) against \(\log _{10}L\) yields approximately a straight line, as is seen in Fig. 4. This behaviour is already seen in the numbers of table 1 of Nield and Kuznetsov (2016). We actually found values of \(a_{\mathrm{{cr}}}\) when \(L=10^{-9},10^{-10},10^{-11}\) and \(10^{-12}\) to be \(a_{\mathrm{{cr}}}=0.01201,0.00671,0.00381\) and 0.00213, respectively.

From Tables 2–4, we see that the value of \(\sigma _i\) (the imaginary part of \(\sigma \)) on the oscillatory curve firstly increases as L decreases, reaches a maximum, and then decreases again with further decrease in L. Tables 2–4 correspond to values on the oscillatory branches of the instability curve shown in Fig. 2 for \(C=1,1.7\) and 2.1 (the dashed lines). We observe that as L becomes very small \(\sigma _i\) likewise becomes very small. This is in complete agreement with the findings of Nield and Kuznetsov (2016) who note in their conclusions (in our notation),...oscillatory instability can still occur as L tends to zero..., in practical situations it is likely that no oscillations will be observed. This behaviour is witnessed in Tables 5–13.

From Tables 5–13, we see that \(\sigma _i\) increases on the oscillatory curve as C increases, and this is in agreement with the exact case of prescribed temperature and concentration where we know the exact solution, cf. Eq. (12).

From Tables 5–13 and the exact solution when \(L=\infty \), we observe that the slope on the stationary convection curve is always 1. However, the slope on the oscillatory convection curve is 0.05 when \(L=\infty ,100\) and then increases to a maximum and then decreases again as \(L\rightarrow 0\). We found approximately, slopes of 0.0524, 0.0561, 0.0606, 0.0633, 0.0567, 0.0522, 0.0502 when \(L=10,5,2.5,1,0.1,0.01,10^{-4}\), respectively, and then for \(L=10^{-6}\) or smaller the slope is 0.05. It appears from the numerical results that the oscillatory curve is a straight line for all values of L, but we have no analysis to justify this. It is worth pointing out that while the oscillatory curve is close to a straight line for an anisotropic inertia coefficient it is not actually straight, see Straughan (2014). Also, the transition from stationary to oscillatory convection in other problems may involve curved stationary convection and oscillatory convection curves, see, e.g. the analysis of Straughan (2015b) when the heat flux is of Cattaneo–Christov type.

In conclusion, we have found the transition from stationary convection to oscillatory convection in the heated below–salted below situation when the Nield and Kuznetsov (2016) boundary conditions, (4), (5), are employed for various values of L. We have chosen for our numerical results the realistic value of \(\epsilon _1=\epsilon Le=20\), although I believe the behaviour found here is not simply restricted to this case. Our results are in agreement with those of Nield and Kuznetsov (2016), and we add further information to their findings.