1 Introduction

Fluid flow through porous media takes place in many practical applications, such as heat exchangers, cooling of electronic components, biological systems, geothermal engineering, solid matrix heat exchangers, enhanced oil recovery, thermal insulation, canopy flow, flow over vegetation, crop fields, grain storage, drying processes and chemical reactors (De Lemos 2009; Ljung et al. 2012; Vafai 2015). High Reynolds numbers, Re, in many of the aforementioned applications have motivated researchers to take into account the effects of turbulence within the pores (Dybbs and Edwards 1984; Khayamyan et al. 2017a, b; Larsson et al. 2018; Seguin et al. 1998). To exemplify, Dybbs and Edwards (1984) categorized the flow into four regimes of pore Re, \( \text{Re}_{p} \), according to: Darcian regime (\( \text{Re}_{p} < 1 \)), Forchheimer regime (\( 1 - 10 < \text{Re}_{p} < 150 \)), unsteady-laminar (\( 150 < \text{Re}_{p} < 300 \)) and turbulent regimes (\( \text{Re}_{p} > 300 \)) based on results from an experimental study of flow through beds of rods, spheres and complex rod bundles. However, experimental measurement and direct numerical simulation of turbulent flow inside the pores in random systems are tricky due to the complexity of the pore structures and their small size. This also implies that the computational effort required to exactly represent these systems is large especially for turbulent flow. A method to circumvent this problem is to replace the complex system of pores with a homogeneous medium with averaged properties using volume averaging techniques (VAT) (Whitaker 2013). Originating from this approach, several versions of macroscopic models are proposed in the literature. In most of these approaches, time averaging is used to model turbulent effects and volume averaging to homogenously present the morphology of the porous medium (Teruel 2009a). It should also be noted that during such averaging processes, extra terms appear that often have to be modeled using experimental measurement or numerical simulation of turbulent flow within the pores. Lee and Howell (1987), Antohe and Lage (1997), Getachew et al. (2000), and Lien and Leschziner (1994) are among those who proposed a two-equation macroscopic turbulence model by Reynolds averaging the volume-averaged Navier–Stokes (VANS) equations. According to Nield (2001), their strategy leads to a model of the macroscale Reynolds stresses, while the intra-pore stresses do not come into play. Another group of researchers such as Nakayama and Kuwahara (1999, 2008), Pedras and de Lemos (2001) and Nikora et al. (2007) applied the volume averaging operator to the Reynolds averaged equations in order to macroscopically model the turbulent flow. As a result, the models derived take into account the intra-pore turbulence in addition to its macroscopic effects. It is shown by Pedras and de Lemos (2001) that the order of time and volume averaging is not important except regarding the turbulence kinetic energy. In addition to the two-equation macroscopic turbulence models mentioned above, other turbulence models have been reported in the literature such as the zero equation model by Masuoka and Takatsu (1996), the one-equation model developed by Alvarez et al. (2003), multi-scale four-equation eddy viscosity model of Kuwata et al. (2014) and Kuwata and Suga’s (2013) based on a second moment closure. Two-equation turbulence models have, however, gained the most attention in the literature similar to their clear fluid counterparts. As compared to clear fluid flow, the transport equations of turbulent kinetic energy (TKE) and dissipation rate equations for porous media flow include additional terms which quantify the effects of the solid matrix on the turbulent parameters. Different correlations have been proposed in the literature to model these extra production terms (Nakayama and Kuwahara 1999, 2008; Pedras and de Lemos 2001). A comparison of the extra terms in TKE and dissipation rate equations from different models is presented in Guo et al. (2006). By a comparison of the results to experimental data, it is shown that the Nakayama and Kuwahara’s (1999) (N–K) model produces more reasonable results as compared to the other models investigated in their study. The original N–K model (Nakayama and Kuwahara 1999) and its modifications have been extensively used in different applications (Chandesris et al. 2006; Hoffmann 2004; Jouybari et al. 2018).

In spite of the extensive works mentioned above on turbulent flow in porous media, much is still unknown including an uncertainty on the existence of large structures in the flow. Several researches have reported that the pore size of the porous medium sets the upper limit of the size of turbulent eddies since these structures become confined in the pores (Jin and Kuznetsov 2017; Jin et al. 2015; Nield 1991; Uth et al. 2016). However, Uth et al. (2016) reported that large structures may exist in porous media with very large porosities equal to 0.995 which is discussed to be unrealistic by Jin and Kuznetsov (2017). Also, direct numerical simulations (DNS) performed by Chandesris et al. (2013) and Breugem and Boersma (2005) for turbulent flow in a channel partially filled with a porous medium showed that large structures forming above a porous–fluid interface penetrate into the upper layer of the porous bed. In order to capture these large structures and considering the analogy between the filtered equations of large eddy simulations (LES) with VANS equations in porous media, Breugem et al. (2006) simulated turbulent flow over and inside a packed bed in a channel using LES. The filter size was considered sufficiently small so that the subfilter-scale dispersion in the channel region was negligible in their study. Breugem et al. (2006) showed that the residual stresses in porous media are small for their case. Obviously, this assumption may not be valid when the Re in the pores is so high that turbulent effects are not negligible. LES modeling of turbulent flow within and over forests as porous media have also been previously reported in several studies including Dwyer et al. (1997), Kanda and Hino (1994), Shaw and Patton (2003) and Watanabe (2004).

Based on the introduction above, the aim of the present study is to present a subgrid-scale model for the intra-pore residual stresses that emerge in the VANS equations. To this end, a model is proposed based on filtered kinetic energy balance within the pores. One advantage with this model is that prior numerical simulations of turbulent flow within the pores are not required in order to close the macroscopic equations. For cases where large structures are present, the VANS equations directly represent the larger motions, whereas the residual motions in the REV are captured with the subgrid-scale model. Otherwise, if there is microscopic turbulence and no macroscopic turbulence, the subgrid-scale model accounts for the turbulence effects within the pores and the VANS equations will be solved in the same way as in laminar flows. Therefore, no turbulence model is used for the macroscopic turbulence and no extra equation is solved for turbulent quantities such as TKE and dissipation rate.

2 Governing Equations

2.1 Filtered Equations

The governing equations for the filtered field when turbulence is modeled with LES and the flow is treated as incompressible are obtained by applying a filtering operation to the continuity and Navier–stokes equations as follows:

$$ \frac{{\partial \overline{U}_{i} }}{{\partial x_{j} }} = 0 $$
(1)
$$ \frac{{\partial \overline{U}_{j} }}{\partial t} + \frac{{\partial \overline{U}_{i} \overline{U}_{j} }}{{\partial x_{i} }} = - \frac{1}{\rho }\frac{{\partial \bar{p}}}{{\partial x_{j} }} + \upsilon \frac{{\partial^{2} \overline{U}_{j} }}{{\partial x_{i} \partial x_{i} }} - \frac{{\partial \tau_{ij}^{r} }}{{\partial x_{i} }} $$
(2)

The filtered mass and momentum equations can be solved with a residual stress model so that \( \tau_{ij}^{r} = \overline{{U_{i} U_{j} }} - \overline{U}_{i} \overline{U}_{j} \) can be evaluated. As mentioned in Pope (2000), the filter type and width, \( \Delta \), do not appear explicitly in Eqs. (1) and (2). They indirectly affect the filtered velocity through the model for the residual stresses. Several subgrid-scale models are proposed for \( \tau_{ij}^{r} \) in the literature to close the filtered equations. The model proposed by Smagorinsky is the simplest one which is based on a linear viscosity model (Pope 2000), as:

$$ \tau_{ij}^{r} = - 2\upsilon_{r} \bar{S}_{ij} $$
(3)

where \( \bar{S}_{ij} = \frac{1}{2}\left( {\frac{{\partial \overline{{U_{i} }} }}{{\partial x_{j} }} + \frac{{\partial \overline{{U_{j} }} }}{{\partial x_{i} }}} \right) \) and \( \upsilon_{r} \) are the filtered rate of the strain tensor and the eddy viscosity of the residual motions, respectively. This model also forms the basis for other more complex models. Using the mixing-length analogy, the eddy viscosity is formulated as:

$$ \upsilon_{r} = \ell_{s}^{2} \bar{S} = \left( {C_{s} \Delta } \right)^{2} \bar{S} $$
(4)

where \( \bar{S} \equiv \left( {2\overline{S}_{ij} \overline{S}_{ij} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \) and \( \ell_{s}^{{}} \) are the characteristics filtered rate of strain and the Smagorinsky length scale, respectively. The latter is assumed to be proportional to \( \Delta \) through the Smagorinsky constant, \( C_{s} \) (Pope 2000). Δ is the filter cut-off width that defines the limit for the size of eddies which are resolved and those that are modeled. It is usually selected to be of the same order of the grid size (Versteeg and Malalasekera 2007). Assuming the grid cells with different length \( \Delta _{x} \), width \( \Delta _{y} \) and height \( \Delta _{z} \), the cut-off width is calculated as the cubic root of the cell volume as:

$$ \Delta = \sqrt[3]{{\Delta _{x}\Delta _{y}\Delta _{z} }} $$
(5)

According to Pope (2000), the size of Δ should be selected such that at least 80% of energy is resolved.

2.2 Volume-Averaged Equations for Flows in Porous Media

According to Breugem and Boersma (2005), the superficial average of an arbitrary parameter \( \varphi \) within a porous medium can be expressed as:

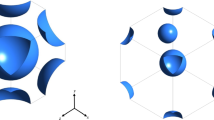
$$ \left\langle \varphi \right\rangle_{\varvec{x}}^{\varepsilon } = \int_{V} {\gamma (\varvec{r})m(\varvec{y})} \varphi (\varvec{r}){\text{d}}V $$
(6)

where \( \left\langle \, \right\rangle_{\varvec{x}}^{\varepsilon } \) denotes the superficial average at the centroid x of a REV with a volume of V, \( \varvec{y = r} - \varvec{x} \) is the relative position, \( \gamma \) is the phase indicator being 1 in the fluid phase and 0 in the solid phase and m is the weighting function. A schematic of a REV for a random porous media is shown in Fig. 1 for which the REV is a sphere with radius \( r_{0} \) where m is defined as:

$$ m(\varvec{y}) = \left\{ \begin{aligned} & 3/\left( {4\pi r_{0}^{3} } \right),\quad \left| \varvec{y} \right| \le r_{0} \\ & 0,\quad \left| \varvec{y} \right| \le r_{0} \, \\ \end{aligned} \right.. $$
(7)
Fig. 1
figure 1

Averaging volume (REV) in volume averaging

Full size image

Applying the volume averaging operator to a general parameter \( \varphi \) results in

$$ \varphi = \left\langle \varphi \right\rangle + {}^\backprime \varphi $$
(8)

where \( {}^\backprime \varphi \) denotes deviation from the averaged value of \( \varphi \) or subfilter-scale\( \varphi \) in LES terminology. Also, \( {{\left\langle \varphi \right\rangle = \left\langle \varphi \right\rangle^{\varepsilon } } \mathord{\left/ {\vphantom {{\left\langle \varphi \right\rangle = \left\langle \varphi \right\rangle^{\varepsilon } } \varepsilon }} \right. \kern-0pt} \varepsilon } \) in Eq. (8) is the intrinsic average of \( \varphi \) and \( \varepsilon \) denotes the porosity of the porous medium, which is defined as:

$$ \varepsilon \left( \varvec{x} \right) \equiv \int_{V} {\gamma (\varvec{r})m(\varvec{y})} {\text{d}}V. $$
(9)

The volume-averaged continuity and Navier–stokes equations for incompressible flows in porous media is simply obtained by applying the volume averaging operator to these equations (Whitaker 2013), according to

$$ \frac{{\partial \varepsilon \left\langle {U_{i} } \right\rangle }}{{\partial x_{j} }} = 0 $$
(10)
$$ \frac{{\partial \left\langle {U_{j} } \right\rangle }}{\partial t} + \frac{1}{\varepsilon }\frac{\partial }{{\partial x_{i} }}\left( {\varepsilon \left\langle {U_{i} } \right\rangle \left\langle {U_{j} } \right\rangle } \right) = - \frac{1}{\varepsilon \rho }\frac{\partial }{{\partial x_{j} }}\left( {\varepsilon \left\langle p \right\rangle } \right) + \frac{\upsilon }{\varepsilon }\frac{{\partial^{2} \left( {\varepsilon \left\langle {U_{j} } \right\rangle } \right)}}{{\partial x_{i} \partial x_{i} }} - \frac{1}{\varepsilon }\frac{{\partial \left( {\varepsilon \tau_{ij}^{p} } \right)}}{{\partial x_{i} }} + f_{j} $$
(11)

where \( \tau_{ij}^{p} \) at high Re corresponds to the intra-pore stresses arising from turbulent motions within the pores of the porous medium since the size of the filter in the volume averaging approach is equal to one REV consisting of at least 10–15 pores (Qin and Hassanizadeh 2015). It is known as residual stress or subgrid-scale stresses using LES terminology. It is defined as:

$$ \tau_{ij}^{p} = \left\langle {U_{i} U_{j} } \right\rangle - \left\langle {U_{i} } \right\rangle \left\langle {U_{j} } \right\rangle \approx \left\langle {{}^\backprime U_{i} {}^\backprime U_{j} } \right\rangle . $$
(12)

The \( f_{j} \) in Eq. (11) represents the drag force per unit mass exerted by the solid matrix on the fluid passing through the porous medium and is given by:

$$ f_{j} = - \frac{\upsilon }{K}\varepsilon \left\langle {U_{j} } \right\rangle - b\varepsilon^{2} \left( {\left\langle {U_{i} } \right\rangle \left\langle {U_{i} } \right\rangle } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left\langle {U_{j} } \right\rangle $$
(13)

where \( b \) and \( K \) are the pressure drag constant and permeability of the porous medium, respectively. As can be observed, the VANS equations and filtered equations are similar since the last term on the RHS of Eq. (11) which corresponds to the drag force is zero for fluid flow outside of porous media (\( \varepsilon = 1 \) and \( f = 0 \) since \( K \to \infty \)). However, the difference lies in the terms representing the residual motion, \( \tau_{ij}^{r} \) and \( \tau_{ij}^{p} \) in Eqs. (2) and (10), respectively. While \( \tau_{ij}^{r} \) in Eq. (2) is modeled to consider the effects of small-scale motions in clear flow, \( \tau_{ij}^{p} \) in VANS momentum equation, Eq. (11) has to be modeled so that it takes into account the turbulent effects within the pores. Breugem et al. (2006) used the equations presented above to study turbulent flow in a channel partially filled with porous media. They showed that the \( \tau_{ij}^{p} \) term is negligible compared to the drag force or other stresses for the case they studied and its effect was therefore not taken into account. However, it is reasonable to think that \( \tau_{ij}^{p} \) matters for high Re turbulent flow in porous media.

2.2.1 Modeling of Subfilter-Scale Stress in Porous Media

In order to close the VANS equations in turbulent flow, a correlation has to be presented for the subfilter-scale stresses in terms of volume-averaged quantities. Similar to the steps followed to model the residual stress in the LES formulation, \( \tau_{ij}^{p} \) is correlated with the volume-averaged strain rate tensor using the linear eddy viscosity model, according to:

$$ \tau_{ij}^{p} = - 2\upsilon_{r\varepsilon } \left\langle {S_{ij} } \right\rangle $$
(14)

where the volume-averaged strain rate tensor is defined as:

$$ \left\langle {S_{ij} } \right\rangle = \frac{1}{2}\left( {\frac{{\partial \left\langle {U_{i} } \right\rangle }}{{\partial x_{j} }} + \frac{{\partial \left\langle {U_{j} } \right\rangle }}{{\partial x_{i} }}} \right). $$
(15)

Now, the closure problem reduces to the calculation of \( \upsilon_{r\phi } \) within the pores. Since structures larger than the REV are solved directly by using the VANS equations, \( \upsilon_{r\phi } \) corresponds to sub-REV stresses within the pores. Turbulent quantities within the pores have been derived by several researchers such as Nakayama and Kuwahara (1999, 2008), Pedras and de Lemos (2001), Teruel and Uddin (2009b) and Chandesris et al. (2006) to close their macroscopic turbulence models. Table 1 summarizes the turbulent quantities and the pore-scale residual stress calculated from these quantities proposed by Nakayama and Kuwahara (1999) and Nakayama and Kuwahara (2008) for their macroscopic \( k - \varepsilon \) model. However, the \( \upsilon_{r\phi } \) will be calculated based on the Smagorinsky model in the present study as:

$$ \upsilon_{r\varepsilon } = \ell_{s}^{2} \left\langle S \right\rangle = \left( {C_{s} d_{p} } \right)^{2} (2\left\langle {S_{ij} S_{ij} } \right\rangle )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} . $$
(16)

where \( \Delta \) in Eq. (4) is substituted by \( d_{\text{p}} \) in Eq. (16) for turbulent flow in porous media. The \( \left\langle {S_{ij} S_{ij} } \right\rangle \) is expressed as:

$$ \left\langle {S_{ij} S_{ij} } \right\rangle = \left\langle {S_{ij} } \right\rangle \left\langle {S_{ij} } \right\rangle + \left\langle {{}^\backprime S_{ij} {}^\backprime S_{ij} } \right\rangle $$
(17)
Table 1 Extra source terms in turbulence equations
Full size table

It can be assumed that in the Smagorinsky model for clear fluid, the second term on the RHS of Eq. (17) can be neglected due to its minor effect on the residual stresses as compared to the first term. However, as mentioned by Nakayama and Kuwahara (2008), the characteristics filtered strain rate (the first term on the RHS of Eq. (17) is negligible compared to the characteristics residual strain rate (the second term on the RHS of Eq. (17)) for turbulent flow in porous media.

2.2.1.1 Evaluation of Characteristics Residual Strain Rate

Consider fluid flow passing through a pore in a porous medium and considering a filter width being much smaller than the pore size, the kinetic energy of the filtered field within the pore is given by:

$$ \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D} E_{f} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D} t}} - \frac{\partial }{{\partial x_{i} }}\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U}_{j} \left( {2\upsilon \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} - \tau_{ij}^{r} - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} }}{\rho }\delta_{ij} } \right)} \right] = - 2\upsilon \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} + \tau_{ij}^{r} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} . $$
(18)

To distinguish between the filtered equations shown in Eqs. (1) and (2) and filtered equations in the pore of a porous medium, the filtered velocity field in the pores is denoted by \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U}_{j} \) instead of \( \bar{U}_{j} \) where \( E_{f} = \frac{1}{2}\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} } \cdot \varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} } \) represents the kinetic energy of the filtered velocity field in the pore. The filter size \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Delta } \) within a pore is considered to be too small so that dispersion by the residual motions is negligible. According to Pope (2000), the terms on the LHS of Eq. (18) represent the transport and those on the RHS of the same equation denote the source and sink terms. However, according to Nakayama and Kuwahara (2008), extra terms appear after volume averaging of the pressure term in Eq. (18) similar to that presented in Eq. (13) which are associated with the source/sink terms. Therefore, the pressure term is kept on the LHS along with the terms on the RHS of Eq. (18) for volume averaging. The other terms in Eq. (18) which represent the spatial transport of filtered kinetic energy do not affect the kinetic energy balance within a pore which is in agreement with observation of Jin and Kuznetsov (2017) who showed that the rate of TKE production is in balance with the dissipation rate in each REV. Volume averaging of Eq. (18) results in

$$ \left\langle { - \frac{1}{\rho }\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U}_{j} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} }}{{\partial x_{j} }} - 2\left( {\upsilon + \upsilon_{r} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{ij} } \right\rangle \approx 0. $$
(19)

Since \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Delta } \) is too small, it can be assumed that \( \left\langle {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } } \right\rangle = \left\langle \varphi \right\rangle \) for a general parameter \( \varphi \). After expanding the terms as proposed in Nakayama and Kuwahara (2008), the following expression will be obtained for residual characteristics residual strain rate

$$ \begin{aligned} 2\upsilon_{r\varepsilon } \left\langle {{}^\backprime S_{ij} {}^\backprime S_{ij} } \right\rangle & \approx - \frac{1}{\rho }\left\langle {U_{j} } \right\rangle \frac{\partial \left\langle p \right\rangle }{{\partial x_{j} }} \approx \varepsilon^{2} b\left( {\left\langle {U_{j} } \right\rangle \left\langle {U_{j} } \right\rangle } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \\ \left\langle {{}^\backprime S_{ij} {}^\backprime S_{ij} } \right\rangle & \approx \frac{{\varepsilon^{2} b\left( {\left\langle {U_{j} } \right\rangle \left\langle {U_{j} } \right\rangle } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}{{2\upsilon_{r\varepsilon } }}. \\ \end{aligned} $$
(20)

Substituting \( \left\langle {{}^\backprime S_{ij} {}^\backprime S_{ij} } \right\rangle \) into Eqs. (16) and (17) yields

$$ \upsilon_{r\varepsilon }^{{}} = \left( {C_{s} d_{p} } \right)^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}}} \left( {\varepsilon^{2} b\left( {\left\langle {U_{j} } \right\rangle \left\langle {U_{j} } \right\rangle } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} . $$
(21)

where a \( C_{s} \) value of 0.1 is chosen which has been reported according to ANSYS Fluent (2015). Nakayama and Kuwahara (2008) proposed the approach described above to compute the extra source terms appearing after volume averaging of TKE and dissipation rate equations in porous media. In order to measure the validity of Eq. (21) in the case of fully turbulent flow in porous media, the eddy viscosity of residual stress calculated by Eq. (21) is compared with the macroscopically fully turbulent flow through two types of porous media in the following section. The mean shear is considered to be zero, and therefore, the macroscopic Reynolds stresses are negligible for this condition. Consequently, the reported eddy viscosities are mainly due to pore-scale stresses. The values used to compare the present results were obtained for the same condition.

3 Evaluation of \( \upsilon_{r\varepsilon }^{{}} \) for Two Types of Porous Media

3.1 Turbulent Flow in a Packed Bed

For a packed bed with the particle diameter of D, the following expressions may be formed (Nakayama and Kuwahara 2008; Seguin et al. 1998):

$$ K = \frac{{\varepsilon^{3} }}{{150\left( {1 - \varepsilon } \right)^{2} }}D^{2} $$
(22)
$$ b = \frac{{1.75\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} D}} $$
(23)
$$ d_{p} = \frac{\varepsilon D}{1 - \varepsilon } $$
(24)

where dp is the pore diameter. Substituting these quantities in Eq. (21) yields the subfilter scale stress, as:

$$ \frac{{\upsilon_{r\varepsilon }^{{}} }}{\upsilon } = 0.0566\left( {\frac{\varepsilon }{1 - \varepsilon }} \right)\frac{\left\langle U \right\rangle D}{\upsilon }. $$
(25)

Figure 2 illustrates a comparison between the intra-pore stress, \( \upsilon_{r\varepsilon }^{{}} \), as calculated from Eq. (25) for a packed bed with \( \varepsilon = 0.4 \), as computed with the N–K model (Nakayama and Kuwahara 2008), as calculated from N–K model (Nakayama and Kuwahara 1999) in Guo et al. (2006) and as obtained from experimental measurements in Bey and Eigenberger (1997). As can be observed, the present results are between the results predicted by the N–K model and the experimental measurements for \( \text{Re}_{D} = {{u_{D} D} \mathord{\left/ {\vphantom {{u_{D} D} {\upsilon \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{ > } 300}}} \right. \kern-0pt} {\upsilon \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{ > } 300}} \).

Fig. 2
figure 2

Comparison of the present results with the experimental of Bey and Eigenberger (1997) and (Nakayama and Kuwahara 2008) model for packed beds with \( \varepsilon = 0.4 \)

Full size image

3.2 Turbulent Flow in Staggered Arrangement of Square Cylinders

For a staggered array of square cylinders of size D (Fig. 3), K and b are defined as (Kuwahara et al. 2006):

$$ K = \frac{{\varepsilon^{3} }}{{120\left( {1 - \varepsilon } \right)^{2} }}D^{2} $$
(26)
$$ b = \frac{{2\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} D}} $$
(27)
Fig. 3
figure 3

Staggered array of square cylinders

Full size image

The pore diameter for the staggered array of square cylinders shown in Fig. 2 is defined as:

$$ d_{\text{p}} = 2 \times \left( {H - D} \right) = 2D\left( {\frac{1}{{\sqrt {1 - \varepsilon } }} - 1} \right). $$
(28)

Substituting these quantities into Eq. (21) yields:

$$ \upsilon_{r\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} = \left( {C_{s} 2D\left( {\frac{1}{{\sqrt {1 - \varepsilon } }} - 1} \right)} \right)^{2} \left( {\varepsilon^{2} \frac{{2\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} d}}\left( {\left\langle {U_{j} } \right\rangle \left\langle {U_{j} } \right\rangle } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$
(29)
$$ \frac{{\upsilon_{r\varepsilon }^{{}} }}{\upsilon } = 0.147\left( {\varepsilon \left( {1 - \varepsilon } \right)} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0pt} 3}}} \left( {1 - \sqrt {1 - \varepsilon } } \right)^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}}} \frac{\left\langle U \right\rangle D}{\upsilon }. $$
(30)

A comparison between the non-dimensional pore-scale stress calculated from Eq. (30) with those evaluated from N–K’s (Nakayama and Kuwahara 1999) pore-scale simulation in Fig. 4 illustrates that the present model successfully predicts the value of residual stress in the staggered array of square cylinders.

Fig. 4
figure 4

Comparison of the present results with the N–K (Nakayama and Kuwahara 2008) model for packed beds for \( \varepsilon = 0.3 \), 0.5, 0.7 and 0.9

Full size image

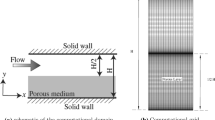
4 Assessment of the Present Model for Turbulent Flow in Wall-Bounded Porous Media

The results of present model will be compared against the DNS results of Jin and Kuznetsov (2017) for turbulent flow in a porous media consisting of spherical particles confined between two walls. The size of the channel, porosity, permeability and form drag coefficient is extracted from those reported in Jin and Kuznetsov (2017). Figure 5 illustrates the geometry considered for numerical simulation. Due to symmetry, only half of the channel is simulated using symmetry boundary condition at the middle. No-slip boundary condition is used for the upper wall and symmetry boundary conditions are adopted for the side walls. The automatic wall function is used on the upper solid wall which helps to accurately capture the near wall turbulence. The inlet and outlet of flow in the x direction are considered to be periodic. Advection terms are discretized using bounded central difference method and second-order Euler backward method is used for the discretization of unsteady terms. The numerical simulations are carried out in Ansys CFX where the present subgrid-scale model is added to include the turbulence effects within the pores. The LES model is selected to capture any possible large structures in the channel. A grid independency study is carried out and it is observed that the velocity profile does not change for an increase in elements from approximately 3200 to 6400. Therefore, 3200 elements are selected for the simulations. Figure 6 shows a comparison between the normalized velocity profiles calculated from the present model and DNS case A in Jin and Kuznetsov 2017. This case is a porous medium with \( {s \mathord{\left/ {\vphantom {s d}} \right. \kern-0pt} d} = 0.75 \), \( \varepsilon = 0.69 \), \( {H \mathord{\left/ {\vphantom {H s}} \right. \kern-0pt} s} = 40 \) and \( \text{Re} = {{u_{D} d} \mathord{\left/ {\vphantom {{u_{D} d} \upsilon }} \right. \kern-0pt} \upsilon } = 257 \) which correspond to channel Re of \( \text{Re} = {{u_{D} 2H} \mathord{\left/ {\vphantom {{u_{D} 2H} \upsilon }} \right. \kern-0pt} \upsilon } = 15400 \). The results are obtained at the large time interval for which the time averaging velocity is independent of the time of starting the averaging process. This time interval has been checked for different starting times of averaging process in order to verify the independency of the final results. It should be noted that no large structures are observed in the present simulations which are in agreement with Jin and Kuznetsov (2017), Jin et al. (2015), Nield (1991) and Uth et al. (2016). Therefore, the main turbulent effects are mainly due to turbulence within the pores. As can be observed in Fig. 6, the present results are in a good agreement with the normalized velocity calculated from the DNS data in Jin and Kuznetsov (2017). As a final comparison, Fig. 7 illustrates \( {{\partial \left( {\varepsilon \left\langle {u^{\prime}v^{\prime}} \right\rangle } \right)} \mathord{\left/ {\vphantom {{\partial \left( {\varepsilon \left\langle {u^{\prime}v^{\prime}} \right\rangle } \right)} {\partial y}}} \right. \kern-0pt} {\partial y}} \) as calculated from DNS results in Jin and Kuznetsov (2017), model results in Jin and Kuznetsov (2017) which are calculated from \( \upsilon_{r\varepsilon } = {{c_{\mu } \left\langle k \right\rangle^{2} } \mathord{\left/ {\vphantom {{c_{\mu } \left\langle k \right\rangle^{2} } {\left\langle {\varepsilon_{\text{d}} } \right\rangle }}} \right. \kern-0pt} {\left\langle {\varepsilon_{\text{d}} } \right\rangle }} \) assuming that the TKE, \( k \), and dissipation rate, \( \varepsilon_{\text{d}} \), are those calculated from DNS results and the present results from Eq. (25). As can be seen, the present results are in a good agreement with the model results in Jin and Kuznetsov (2017). Due to negligible velocity gradient in most of the channel height, a small amount of Reynolds stress is calculated from eddy viscosity except for the region close to the wall where the velocity gradient takes large values. Consequently, both of the present model results and model results of Jin and Kuznetsov (2017) increase close to the wall which agree reasonably well with the DNS data of Jin and Kuznetsov (2017).

Fig. 5
figure 5

Porous channel with upper and lower solid wall

Full size image
Fig. 6
figure 6

Normalized velocity profile from Jin and Kuznetsov (2017) and the present study

Full size image
Fig. 7
figure 7

Comparison of \( {{\partial \left( {\varepsilon \left\langle {u^{\prime}v^{\prime}} \right\rangle } \right)} \mathord{\left/ {\vphantom {{\partial \left( {\varepsilon \left\langle {u^{\prime}v^{\prime}} \right\rangle } \right)} {\partial y}}} \right. \kern-0pt} {\partial y}} \) normalized by \( g_{1} \) calculated from the present model and those of Jin and Kuznetsov (2017) for case A

Full size image

5 Conclusion

Due to the similarity between the filtered Navier–stokes and VANS equations within porous media, it is found that these equations may be used to directly solve the large structures of turbulence provided that a proper model for the subgrid-scale is adopted. To this end, the filtered kinetic energy within the pores in a REV is re-examined to reach a balance between the production and dissipation terms in the pores. As a result, a subfilter-scale model for the residual stresses in porous media is presented without a need of doing a prerequisite numerical simulation of turbulent flow within the pores. The present model is validated with numerical and experimental results from the literature for packed beds and staggered array of square cylinders. The present model is also used to model turbulent flow in a wall-bounded porous media. Although no large structures are observed in the domain, the present subgrid-scale model successfully predicts the level of subgrid Reynolds stress close to the wall and within the porous medium.