Skip to main content
SpringerLink
Log in

Porous Media Characterization Using Minkowski Functionals: Theories, Applications and Future Directions

  • Published:
Transport in Porous Media Aims and scope Submit manuscript

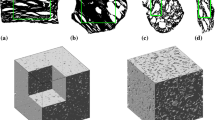
Abstract

An elementary question in porous media research is in regard to the relationship between structure and function. In most fields, the porosity and permeability of porous media are properties of key interest. There is, however, no universal relationship between porosity and permeability since not only does the fraction of void space matter for permeability but also the connectivity of the void fraction. With the evolution of modern day X-ray microcomputed tomography (micro-CT) and advanced computing, it is now possible to visualize porous media at an unprecedented level of detail. Approaches in analyzing micro-CT data of porous structures vary in the literature from phenomenological characterization to network analysis to geometrical and/or topological measurements. This leads to a question about how to consistently characterize porous media in a way that facilitates theoretical developments. In this effort, the Minkowski functionals (MF) emerge from the field of statistical physics where it is evident that many physical processes depend on the geometry and topology of bodies or multiple bodies in 3D space. Herein we review the theoretical basis of the MF, mathematical theorems and methods necessary for porous media characterization, common measurement errors when using micro-CT data and recent findings relating the MF to macroscale porous media properties. This paper is written to provide the basics necessary for porous media characterization and theoretical developments. With the wealth of information generated from 3D imaging of porous media, it is necessary to develop an understanding of the limitations and opportunities in this exciting area of research.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Abbena, E., Salamon, S., Gray, A.: Modern Differential Geometry of Curves and Surfaces with Mathematica. CRC Press, Boca Raton (2017)

    Google Scholar 

  • Adler, P.M., Jacquin, C.G., Thovert, J.F.: The formation factor of reconstructed porous media. Water Resour. Res. 28(6), 1571 (1992)

    Google Scholar 

  • Anderson, E.J., Kreuzer, S.M., Small, O., Tate, M.L.K.: Pairing computational and scaled physical models to determine permeability as a measure of cellular communication in micro-and nano-scale pericellular spaces. Microfluid. Nanofluid. 4(3), 193 (2008)

    Google Scholar 

  • Andersson, L.: Defining a novel pore-body to pore-throat morphological aspect ratio that scales with residual non-wetting phase capillary trapping in porous media. Adv. Water Resour. (2018)

  • Ardanza-Trevijano, S., Zuriguel, I., Arvalo, R., Maza, D.: Topological analysis of tapped granular media using persistent homology. Phys. Rev. E 89(5), 052212 (2014). https://doi.org/10.1103/PhysRevE.89.052212

    Article  Google Scholar 

  • Armstrong, R.T., Porter, M.L., Wildenschild, D.: Linking pore-scale interfacial curvature to column-scale capillary pressure. Adv. Water Resour. 46, 55 (2012)

    Google Scholar 

  • Armstrong, R.T., Georgiadis, A., Ott, H., Klemin, D., Berg, S.: Critical capillary number: desaturation studied with fast X-ray computed microtomography. Geophys. Res. Lett. 41(1), 55 (2014)

    Google Scholar 

  • Armstrong, R.T., McClure, J.E., Berrill, M.A., Rücker, M., Schlüter, S., Berg, S.: Beyond Darcy’s law: the role of phase topology and ganglion dynamics for two-fluid flow. Phys. Rev. E 94(4), 043113 (2016)

    Google Scholar 

  • Arns, C.H., Knackstedt, M.A., Pinczewski, W.V., Mecke, K.R.: Euler-Poincaré characteristics of classes of disordered media. Phys. Rev. E 63(3), 031112 (2001)

    Google Scholar 

  • Bañados, M., Teitelboim, C., Zanelli, J.: Black hole entropy and the dimensional continuation of the Gauss-Bonnet theorem. Phys. Rev. Lett. 72(7), 957 (1994)

    Google Scholar 

  • Bear, J.: Dynamics of Fluids in Porous Media. Courier Corporation, North Chelmsford (2013)

    Google Scholar 

  • Berg, S., Ott, H., Klapp, S.A., Schwing, A., Neiteler, R., Brussee, N., Makurat, A., Leu, L., Enzmann, F., Schwarz, J.O., et al.: Real-time 3D imaging of Haines jumps in porous media flow. Proc. Nat. Acad. Sci. 110(10), 3755 (2013)

    Google Scholar 

  • Berg, S., Rücker, M., Ott, H., Georgiadis, A., van der Linde, H., Enzmann, F., Kersten, M., Armstrong, R., Becker, J., Wiegmann, A., et al.: Connected pathway relative permeability from pore-scale imaging of imbibition. Adv. Water Resour. 90, 24 (2016)

    Google Scholar 

  • Bijeljic, B., Mostaghimi, P., Blunt, M.J.: Signature of non-Fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 107(20), 204502 (2011)

    Google Scholar 

  • Blunt, M.J.: Multiphase Flow in Permeable Media: A Pore-Scale Perspective. Cambridge University Press, Cambridge (2017)

    Google Scholar 

  • Blunt, M.J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., Paluszny, A., Pentland, C.: Pore-scale imaging and modelling. Adv. Water Resour. 51, 197 (2013)

    Google Scholar 

  • Carlsson, G.: Topology and data. Bull. Am. Math. Soc. 46(2), 255 (2009)

    Google Scholar 

  • Carlsson, G., Zomorodian, A.: The theory of multidimensional persistence. Discrete Comput. Geom. 42(1), 71 (2009). https://doi.org/10.1007/s00454-009-9176-0

    Article  Google Scholar 

  • Cerri, A., Fabio, B.D., Ferri, M., Frosini, P., Landi, C.: Betti numbers in multidimensional persistent homology are stable functions. Math. Methods Appl. Sci. 36(12), 1543 (2013). https://doi.org/10.1002/mma.2704

    Article  Google Scholar 

  • Cohen-Steiner, D., Edelsbrunner, H., Harer, J.: Stability of persistence diagrams. Discrete Comput. Geom. 37, 103 (2007)

    Google Scholar 

  • Darcy, H.: Les fontaines publiques de la ville de Dijon: exposition et application... (Victor Dalmont, 1856)

  • Delgado-Friedrichs, O., Robins, V., Sheppard, A.: In: 2014 IEEE International Conference on Image Processing (ICIP) (2014), pp. 4872–4876. https://doi.org/10.1109/ICIP.2014.7025987

  • Delgado-Friedrichs, O.: Diamorse—Digital image analysis using discrete Morse theory and persistent homology (2016). https://github.com/AppliedMathematicsANU/diamorse

  • Delgado-Friedrichs, O., Robins, V., Sheppard, A.: Skeletonization and partitioning of digital images using discrete morse theory. IEEE Trans. Pattern Anal. Mach. Intell. 37(3), 654 (2015). https://doi.org/10.1109/TPAMI.2014.2346172

    Article  Google Scholar 

  • Dong, H., Blunt, M.J.: Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 80(3), 036307 (2009)

    Google Scholar 

  • Dullien, F.A.: Porous Media: Fluid Transport and Pore Structure. Academic Press, Cambridge (2012)

    Google Scholar 

  • Edelsbrunner, H., Harer, J.: Persistent homology-a survey. Contemp. Math. 453, 257 (2008)

    Google Scholar 

  • Edelsbrunner, H., Harer, J.: Computational Topology: An introduction. American Mathematical Society, Providence, Rhode Island (2010)

    Google Scholar 

  • Edelsbrunner, H., Letscher, D., Zomorodian, A.: Topological persistence and simplification. Discrete Comput. Geom. 28(4), 511 (2002). https://doi.org/10.1007/s00454-002-2885-2

    Article  Google Scholar 

  • Edelsbrunner, H., Harer, J., Zomorodian, A.: Hierarchical Morse–Smale complexes for piecewise linear 2-manifolds. Discrete Comput Geom 30(1), 87 (2003). https://doi.org/10.1007/s00454-003-2926-5

    Article  Google Scholar 

  • Falconer, R.E., Houston, A.N., Otten, W., Baveye, P.C.: Emergent behavior of soil fungal dynamics: influence of soil architecture and water distribution. Soil Sci. 177(2), 111 (2012)

    Google Scholar 

  • Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93(3), 418 (1959)

    Google Scholar 

  • Fredrich, J., Greaves, K., Martin, J.: Pore geometry and transport properties of Fontainebleau sandstone. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 30, 691–697 (1993)

    Google Scholar 

  • Gray, W.G., Miller, : In: AGEM\(^2\)) (Springer, (ed.) Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems. Advances in Geophysical and Environmental Mechanics and. Mathematics, C.T.: In (2014)

  • Grimm, V.: Ten years of individual-based modelling in ecology: what have we learned and what could we learn in the future? Ecol. Model. 115(2–3), 129 (1999)

    Google Scholar 

  • Groot, S.D., Mazur, P.: Non-Equilibrium Thermodynamics. North-Holland Publishing Company, Oxford (1962)

    Google Scholar 

  • Gyulassy, A.G., Duchaineau, M.A., Natarajan, V., Pascucci, V., Bringa, E.M., Higginbotham, A., Hamann, B.: Topologically clean distance fields. IEEE Trans. Vis. Comput. Gr. 13(6), 1432 (2007). https://doi.org/10.1109/TVCG.2007.70603

    Article  Google Scholar 

  • Gyulassy, A., Bremer, P., Pascucci, V.: Computing Morse–Smale complexes with accurate geometry. IEEE Trans. Vis. Comput. Gr. 18(12), 2014 (2012). https://doi.org/10.1109/TVCG.2012.209

    Article  Google Scholar 

  • Hadwiger, H.: Vorlesungen tiber inhalt, oberfläche und isoperirnetrie (1957)

  • Haines, W.B.: Studies in the physical properties of soil. V. The hysteresis effect in capillary properties, and the modes of moisture distribution associated therewith. J. Agric. Sci. 20(1), 97 (1930)

    Google Scholar 

  • Hansen, A., Sinha, S., Bedeaux, D., Kjelstrup, S., Savani, I., Vassvik, M.: arXiv preprint arXiv:1605.02874 (2016)

  • Herring, A., Robins, V., Saadatfar, M., Young, B. Knackstedt, M., Sheppard, A.: (2018)

  • Herring, A.L., Harper, E.J., Andersson, L., Sheppard, A., Bay, B.K., Wildenschild, D.: Effect of fluid topology on residual nonwetting phase trapping: Implications for geologic CO2 sequestration. Adv. Water Res. 62, 47 (2013)

    Google Scholar 

  • Herring, A.L., Andersson, L., Schlüter, S., Sheppard, A., Wildenschild, D.: Efficiently engineering pore-scale processes: the role of force dominance and topology during nonwetting phase trapping in porous media. Adv. Water Resour. 79, 91 (2015)

    Google Scholar 

  • Hilfer, R.: Macroscopic capillarity and hysteresis for flow in porous media. Phys. Rev. E 73(1), 016307 (2006)

    Google Scholar 

  • Hilpert, M., Miller, C.T.: Pore-morphology-based simulation of drainage in totally wetting porous media. Adv. Water Resour. 24(3–4), 243 (2001)

    Google Scholar 

  • Hilpert, M., Miller, C.T., Gray, W.G.: Stability of a fluid-fluid interface in a biconical pore segment. J. Colloid Interface Sci. 267(2), 397 (2003)

    Google Scholar 

  • Hiraoka, Y., Nakamura, T., Hirata, A., Escolar, E.G., Matsue, K., Nishiura, Y.: In: Proceedings of the National Academy of Sciences p. 201520877 (2016)

  • Hyde, S., Barnes, I., Ninham, B.: Curvature energy of surfactant interfaces confined to the plaquettes of a cubic lattice. Langmuir 6(6), 1055 (1990)

    Google Scholar 

  • Iglauer, S., Paluszny, A., Pentland, C.H., Blunt, M.J.: Residual CO2 imaged with X-ray micro-tomography. Geophys. Res. Lett. 38(21) (2011)

    Article  Google Scholar 

  • Iuricich, F., Scaramuccia, S., Landi, C., L., : De Floriani, in SIGGRAPH ASIA 2016 Symposium on Visualization (ACM, vol, vol. SA ’16, p. pp. 5:1–5:, 8, New York, NY, USA (2016). https://doi.org/10.1145/3002151.3002166

  • Jiao, Y., Stillinger, F., Torquato, S.: A superior descriptor of random textures and its predictive capacity. Proc. Nat. Acad. Sci. 106(42), 17634 (2009)

    Google Scholar 

  • Jones, A.C., Milthorpe, B., Averdunk, H., Limaye, A., Senden, T.J., Sakellariou, A., Sheppard, A.P., Sok, R.M., Knackstedt, M.A., Brandwood, A., et al.: Analysis of 3D bone ingrowth into polymer scaffolds via micro-computed tomography imaging. Biomaterials 25(20), 4947 (2004)

    Google Scholar 

  • Jones, A.C., Arns, C.H., Sheppard, A.P., Hutmacher, D.W., Milthorpe, B.K., Knackstedt, M.A.: Assessment of bone ingrowth into porous biomaterials using MICRO-CT. Biomaterials 28(15), 2491 (2007)

    Google Scholar 

  • Kac, M.: Can one hear the shape of a drum? Am. Math. Mon. 73(4), 1 (1966)

    Google Scholar 

  • Kapfer, S.C., Hyde, S.T., Mecke, K., Arns, C.H., Schröder-Turk, G.E.: Minimal surface scaffold designs for tissue engineering. Biomaterials 32(29), 6875 (2011)

    Google Scholar 

  • Karadimitriou, N., Hassanizadeh, S., Joekar-Niasar, V., Kleingeld, P.: Micromodel study of two-phase flow under transient conditions: quantifying effects of specific interfacial area. Water Resour. Res. 50(10), 8125 (2014)

    Google Scholar 

  • Katz, A., Thompson, A.: Quantitative prediction of permeability in porous rock. Phys. Rev. B 34(11), 8179 (1986)

    Google Scholar 

  • Khanamiri, H., Berg, C.F., Slotte, P.A.,Torster, O., Schlẗer, S.: Description of free energy for immiscibletwo-fluid flow in porous media by integral geometry andthermodynamics. Water Res. Res. (in press)

  • Khanamiri, H.H., Torsæter, O.: Water Resour. Res

  • Kimura, M., Obayashi, I., Takeichi, Y., Murao, R., Hiraoka, Y.: Non-empirical identification of trigger sites in heterogeneous processes using persistent homology. Sci. Rep. 8(1), 3553 (2018). https://doi.org/10.1038/s41598-018-21867-z

    Article  Google Scholar 

  • Klain, D.A.: A short proof of Hadwiger’s characterization theorem. Mathematika 42(2), 329 (1995)

    Google Scholar 

  • Knackstedt, M.A., Arns, C.H., Senden, T.J., Gross, K.: Structure and properties of clinical coralline implants measured via 3D imaging and analysis. Biomaterials 27(13), 2776 (2006)

    Google Scholar 

  • Knothe, M.T.: Whither flows the fluid in bone? An osteocyte’s perspective. J. Biomech. 36(10), 1409 (2003)

    Google Scholar 

  • Koebernick, N., Weller, U., Huber, K., Schlüter, S., Vogel, H.J., Jahn, R., Vereecken, H., Vetterlein, D.: In situ visualization and quantification of three-dimensional root system architecture and growth using X-ray computed tomography. Vadose Zone J 13(8) (2014)

    Article  Google Scholar 

  • Kramar, M., Goullet, A., Kondic, L., Mischaikow, K.: Quantifying force networks in particulate systems. Phys. D: Nonlinear Phenom. 283, 37 (2014). https://doi.org/10.1016/j.physd.2014.05.009

    Article  Google Scholar 

  • Kramar, M., Levanger, R., Tithof, J., Suri, B., Xu, M., Paul, M., Schatz, M.F., Mischaikow, K.: Topology in dynamics, differential equations, and data. Phys. D: Nonlinear Phenom. 334, 82 (2016). https://doi.org/10.1016/j.physd.2016.02.003

    Article  Google Scholar 

  • Kumahor, S., de Rooij, G., Schlüter, S., Vogel, H.J.: Water flow and solute transport in unsaturated sanda—comprehensive experimental approach. Vadose Zone J. 14(2) (2015)

    Article  Google Scholar 

  • Laney, D., Bremer, P.T., Mascarenhas, A., Miller, P., Pascucci, V.: Understanding the structure of the turbulent mixing layer in hydrodynamic instabilities. IEEE Trans. Vis. Comput. Graph. 12, 1053 (2006)

    Google Scholar 

  • Lang, C., Ohser, J., Hilfer, R.: On the analysis of spatial binary images. J. Microsc. 203(3), 303 (2001)

    Google Scholar 

  • Lee, Y., Barthel, S.D., Dłotko, P., Moosavi, S.M., Hess, K., Smit, B.: arXiv preprint arXiv:1701.06953 (2017)

  • Legland, D., Kiêu, K., Devaux, M.F.: Computation of Minkowski measures on 2D and 3D binary images. Image Anal. Stereol. 26(2), 83 (2011)

    Google Scholar 

  • Leverett, M., et al.: Capillary behavior in porous solids. Trans. AIME 142(01), 152 (1941)

    Google Scholar 

  • Li, T., Schlüter, S., Dragila, M.I., Wildenschild, D.: An improved method for estimating capillary pressure from 3D microtomography images and its application to the study of disconnected nonwetting phase. Adv. Water Resour. 114, 249 (2018)

    Google Scholar 

  • Liu, Z., Herring, A., Robins, V.: R. In: International Symposium of the Society of Core Analysts, Armstrong (2017)

  • Liu, Z., Herring, A., Arns, C., Berg, S., Armstrong, R.T.: Pore-scale characterization of two-phase flow using integral geometry. Transp. Porous Media 118(1), 99 (2017)

    Google Scholar 

  • Mantz, H., Jacobs, K., Mecke, K.: Utilizing Minkowski functionals for image analysis: a marching square algorithm. J. Stat. Mech. Theory Exp. 2008(12), P12015 (2008)

    Google Scholar 

  • Matsumoto, Y.: An Introduction to Morse Theory. AMS Bookstore, Providence, RI (2002)

    Google Scholar 

  • McClure, J.E., Prins, J.F., Miller, C.T.: A novel heterogeneous algorithm to simulate multiphase flow in porous media on multicore CPU–GPU systems. Comput. Phys. Commun. 185(7), 1865 (2014)

    Google Scholar 

  • McClure, J.E., Berrill, M.A., Gray, W.G., Miller, C.T.: Influence of phase connectivity on the relationship among capillary pressure, fluid saturation, and interfacial area in two-fluid-phase porous medium systems. Phys. Rev. E 94(3), 033102 (2016)

    Google Scholar 

  • McClure, J.E., Armstrong, R.T., Berrill, M.A., Schlüter, S., Berg, S., Gray, W.G., Miller, C.T.: Geometric state function for two-fluid flow in porous media. Phys. Rev. Fluids 3, 084306 (2018). https://doi.org/10.1103/PhysRevFluids.3.084306

    Article  Google Scholar 

  • Mecke, K.R.: Integral geometry in statistical physics. Int. J. Mod. Phys. B 12(09), 861 (1998)

    Google Scholar 

  • Mecke, K.R.: Statistical Physics and Spatial Statistics, pp. 111–184. Springer, Berlin (2000)

    Google Scholar 

  • Mecke, K.R., Sofonea, V.: Morphology of spinodal decomposition. Phys. Rev. E 56(4), R3761 (1997)

    Google Scholar 

  • Mecke, K., Wagner, H.: Euler characteristic and related measures for random geometric sets. J. Stat. Phys. 64(3–4), 843 (1991)

    Google Scholar 

  • Michielsen, K., De Raedt, H.: Integral-geometry morphological image analysis. Phys. Rep. 347(6), 461 (2001)

    Google Scholar 

  • Mosser, L., Dubrule, O., Blunt, M.J.: arXiv preprint arXiv:1712.02854 (2017)

  • Nagel, W., Ohser, J., Pischang, K.: An integral-geometric approach for the Euler–Poincaré characteristic of spatial images. J. Microsc. 198(1), 54 (2000)

    Google Scholar 

  • Ohser, J., Mücklich, F.: Statistical Analysis of Microstructures in Materials Science. Wiley, Hoboken (2000)

    Google Scholar 

  • Ohser, J., Redenbach, C., Schladitz, K.: Mesh free estimation of the structure model index. Image Anal. Stereol. 28(3), 179 (2011)

    Google Scholar 

  • Okabe, H., Blunt, M.J.: Pore space reconstruction of vuggy carbonates using microtomography and multiple-point statistics, Water Resour. Res. 43(12) (2007)

  • Okabe, H., Blunt, M.J.: Pore space reconstruction using multiple-point statistics. J. Pet. Sci. Eng. 46(1–2), 121 (2005)

    Google Scholar 

  • Øren, P.E., Bakke, S.: Process based reconstruction of sandstones and prediction of transport properties. Transp. Porous Media 46(2–3), 311 (2002)

    Google Scholar 

  • Øren, P.E., Bakke, S.: Reconstruction of Berea sandstone and pore-scale modelling of wettability effects. J. Pet. Sci. Eng. 39(3–4), 177 (2003)

    Google Scholar 

  • Pentland, C.H., El-Maghraby, R., Iglauer, S., Blunt, M.J.: Measurements of the capillary trapping of super-critical carbon dioxide in Berea sandstone, Geophys. Res. Lett. 38(6) (2011)

    Article  Google Scholar 

  • Picchi, D., Battiato, I.: The Impact of Pore-Scale Flow Regimes on Upscaling of Immiscible Two-Phase Flow in Porous Media. Water Resour. Res. 54(9), 6683–6707 (2018)

    Google Scholar 

  • Porter, M.L., Wildenschild, D., Grant, G., Gerhard, J.I.: Measurement and prediction of the relationship between capillary pressure, saturation, and interfacial area in a NAPL-water-glass bead system. Water Resour. Res. 46(8) (2010)

  • Ramandi, H.L., Mostaghimi, P., Armstrong, R.T., Saadatfar, M., Pinczewski, W.V.: Porosity and permeability characterization of coal: a micro-computed tomography study. Int. J. Coal Geol. 154, 57 (2016)

    Google Scholar 

  • Robins, V.: Towards computing homology from finite approximations. Topol. Proc. 24, 503 (1999)

    Google Scholar 

  • Robins, V., Wood, P.J., Sheppard, A.P.: Theory and algorithms for constructing discrete Morse complexes from grayscale digital images. IEEE Trans. Pattern Anal. Mach. Intell. 33(8), 1646 (2011)

    Google Scholar 

  • Robins, V., Saadatfar, M., Delgado-Friedrichs, O., Sheppard, A.P.: Percolating length scales from topological persistence analysis of micro-CT images of porous materials. Water Resour. Res. 52(1), 315 (2016). https://doi.org/10.1002/2015WR017937

    Article  Google Scholar 

  • Rücker, M., Berg, S., Armstrong, R., Georgiadis, A., Ott, H., Schwing, A., Neiteler, R., Brussee, N., Makurat, A., Leu, L., et al.: From connected pathway flow to ganglion dynamics. Geophys. Res. Lett. 42(10), 3888 (2015)

    Google Scholar 

  • Saadatfar, M., Takeuchi, H., Robins, V., Francois, N., Hiraoka, Y.: Pore configuration landscape of granular crystallization. Nat. Commun. 8, 15082 (2017)

    Google Scholar 

  • Saadatfar, M., Takeuchi, H., Robins, V., Francois, N., Hiraoka, Y.: Pore configuration landscape of granular crystallization, Nature. Nat. Commun. 8, 15082 (2017). https://doi.org/10.1038/ncomms15082

    Article  Google Scholar 

  • Sahimi, M.: Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches. John Wiley & Sons, Hoboken (2011)

    Google Scholar 

  • San Jose Martinez, F., Muñoz, F., Caniego, F., Peregrina, F.: Morphological functions to quantify three-dimensional tomograms of macropore structure in a vineyard soil with two different management regimes. Vadose Zone J. 12(3) (2013)

    Article  Google Scholar 

  • Santaló, L.A.: Integral Geometry and Geometric Probability. Cambridge University Press, Cambridge (2004)

    Google Scholar 

  • Schaap, M.G., Porter, M.L., Christensen, B.S., Wildenschild, D.: Comparison of pressure-saturation characteristics derived from computed tomography and lattice Boltzmann simulations. Water Resour. Res. 43(12) (2007)

  • Scheel, M., Seemann, R., Brinkmann, M., Di Michiel, M., Sheppard, A., Breidenbach, B., Herminghaus, S.: Morphological clues to wet granular pile stability. Nat. Mater. 7(3), 189 (2008)

    Google Scholar 

  • Schlüter, S., Vogel, H.J.: On the reconstruction of structural and functional properties in random heterogeneous media. Adv. Water Resour. 34(2), 314 (2011)

    Google Scholar 

  • Schlüter, S., Weller, U., Vogel, H.J.: Soil-structure development including seasonal dynamics in a long-term fertilization experiment. J. Plant Nutr. Soil Sci. 174(3), 395 (2011)

    Google Scholar 

  • Schlüter, S., Sheppard, A., Brown, K., Wildenschild, D.: Image processing of multiphase images obtained via X-ray microtomography: a review. Water Resour. Res. 50(4), 3615 (2014)

    Google Scholar 

  • Schlüter, S., Berg, S., Rücker, M., Armstrong, R., Vogel, H.J., Hilfer, R., Wildenschild, D.: Pore-scale displacement mechanisms as a source of hysteresis for two-phase flow in porous media. Water Resour. Res. 52(3), 2194 (2016)

    Google Scholar 

  • Schlüter, S., Henjes, S., Zawallich, J., Bergaust, L., Horn, M., Ippisch, O., Vogel, H.J., Dörsch, P.: Denitrification in soil aggregate analogues-effect of aggregate size and oxygen diffusion. Front. Environ. Sci. 6, 17 (2018)

    Google Scholar 

  • Schmalzing, J., Kerscher, M., Buchert, T.: arXiv preprint astro-ph/9508154 (1995)

  • Schmalzing, J., Górski, K.M.: Minkowski functionals used in the morphological analysis of cosmic microwave background anisotropy maps. Mon. Not. R. Astron. Soc. 297(2), 355 (1998)

    Google Scholar 

  • Schneider, R.: Convex Bodies: the Brunn–Minkowski Theory, 151st edn. Cambridge University Press, Cambridge (2014)

    Google Scholar 

  • Scholz, C., Wirner, F., Götz, J., Rüde, U., Schröder-Turk, G.E., Mecke, K., Bechinger, C.: Permeability of porous materials determined from the Euler characteristic. Phys. Rev. Lett. 109(26), 264504 (2012)

    Google Scholar 

  • Scholz, C., Wirner, F., Klatt, M.A., Hirneise, D., Schröder-Turk, G.E., Mecke, K., Bechinger, C.: Direct relations between morphology and transport in Boolean models. Phys. Rev. E 92(4), 043023 (2015)

    Google Scholar 

  • Serra, J.: Image analysis and mathematical morphology, pp. 424–478. (1982)

  • Serra, J.: Image Analysis and Mathematical Morphology. Academic Press Inc, Cambridge (1983)

    Google Scholar 

  • Tanino, Y., Blunt, M.J.: Capillary trapping in sandstones and carbonates: dependence on pore structure. Water Resour. Res. 48(8) (2012)

  • Tate, M.L.K., Steck, R., Anderson, E.J.: Bone as an inspiration for a novel class of mechanoactive materials. Biomaterials 30(2), 133 (2009)

    Google Scholar 

  • Tiab, D., Donaldson, E.C.: Petrophysics: Theory and Practice of Measuring Reservoir Rock and Fluid Transport Properties. Gulf Professional Publishing, Houston (2015)

    Google Scholar 

  • Ushizima, D., Morozov, D., Weber, G.H., Bianchi, A.G.C., Sethian, J.A., Bethel, E.W.: Augmented topological descriptors of pore networks for material science. IEEE Trans. Vis. Comput. Gr. 18(12), 2041 (2012). https://doi.org/10.1109/TVCG.2012.200

    Article  Google Scholar 

  • Valavanides, M., Payatakes, A.: True-to-mechanism model of steady-state two-phase flow in porous media, using decomposition into prototype flows. Adv. Water Resour. 24(3–4), 385 (2001)

    Google Scholar 

  • Vogel, H.: A numerical experiment on pore size, pore connectivity, water retention, permeability, and solute transport using network models. Eur. J. Soil Sci. 51(1), 99 (2000)

    Google Scholar 

  • Vogel, H.J., Weller, U., Schlüter, S.: Quantification of soil structure based on Minkowski functions. Comput. Geosci. 36(10), 1236 (2010)

    Google Scholar 

  • Wang, Y., Rahman, S.S., Arns, C.H.: Super resolution reconstruction of \(\mu \)-CT image of rock sample using neighbour embedding algorithm. Phys. A Stat. Mech. Appl. 493, 177 (2018)

    Google Scholar 

  • Weyl, H.: On the volume of tubes. Am. J. Math. 61(2), 461 (1939)

    Google Scholar 

  • Whitaker, S.: The Method of Volume Averaging, vol. 13. Springer Science & Business Media, Berlin (2013)

    Google Scholar 

  • Wildenschild, D., Sheppard, A.P.: X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 51, 217 (2013)

    Google Scholar 

  • Wildenschild, D., Vaz, C., Rivers, M., Rikard, D., Christensen, B.: Using X-ray computed tomography in hydrology: systems, resolutions, and limitations. J. Hydrol. 267(3–4), 285 (2002)

    Google Scholar 

  • Zhang, Y., Mostaghimi, P., Fogden, A., Sheppard, A., Arena, A., Middleton, J., Armstrong, R.T.: Time-lapsed visualization and characterization of shale diffusion properties using 4D X-ray microcomputed tomography. Energy Fuels 32(3), 2889 (2018)

    Google Scholar 

  • Zomorodian, A., Carlsson, G.: Computing persistent homology. Discrete Comput. Geom. 33(2), 249 (2005)

    Google Scholar 

Download references

Acknowledgements

We thank the Tyree X-Ray Laboratory in the School of Minerals and Energy Resources Engineering, UNSW for assistance with image collection and data processing. Professors Stephen Foster (fiber-reinforced concrete) and Melissa Knothe-Tate and Dr. Tzong-Tyng Hung (mouse leg) are acknowledged for graciously sharing their microtomography data. We thank Ji-Youn Arns and Zhenghuai Guo for their persistence in contrast optimization for the mouse leg and visualization of the fiber-reinforced concrete samples. Funding was provided from the Australian Research Council Discovery Grant DP160104995. VR is supported by ARC Future Fellowship FT140100604. An award of computer time was provided by the Department of Energy INCITE program. This research also used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.

Author information

Authors and Affiliations

  1. School of Minerals and Energy Resoureces Engineering, University of New South Wales, Sydney, 2033, Australia

    Ryan T. Armstrong, Zhishang Liu & Christoph H. Arns

  2. Advanced Research Computing, Virginia Tech, Blacksburg, VA, 24061, USA

    James E. McClure

  3. Research School of Physics and Engineering, Australian National University, Canberra, ACT, 2601, Australia

    Vanessa Robins

  4. Helmholtz-Centre for Environmental Research, Theodor-Lieser-Str. 4, 06120, Halle, Germany

    Steffen Schlüter

  5. Shell Global Solutions International B.V., Kesslerpark 1, 2288 GS, Rijswijk, The Netherlands

    Steffen Berg

  6. Department of Earth Science and Engineering, Department of Chemical Engineering, Imperial College London, London, UK

    Steffen Berg

Authors
  1. Ryan T. Armstrong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James E. McClure
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vanessa Robins
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhishang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Christoph H. Arns
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Steffen Schlüter
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Steffen Berg
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ryan T. Armstrong.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Armstrong, R.T., McClure, J.E., Robins, V. et al. Porous Media Characterization Using Minkowski Functionals: Theories, Applications and Future Directions. Transp Porous Med 130, 305–335 (2019). https://doi.org/10.1007/s11242-018-1201-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11242-018-1201-4

Keywords

Search

Navigation