Asymptotic Analysis of Three-Scale Model of pH-Dependent Flows in 1:1 Clays with Danckwerts’ Boundary Conditions

Abstract

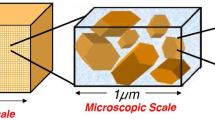
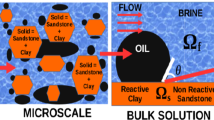
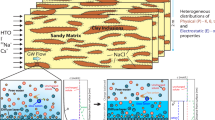
The electroremediation process is an efficient method for removing pollutants from clayey soils. We model this process in kaolinite clays considering three scales—nano, micro and macro—under the assumption of a stratified geometry in conjunction with more realistic Danckwerts’ boundary conditions imposed at the electrodes. The resulting multiscale model is a coupled system of nonlinear partial differential equations. We derive analytical solutions of the macroscopic equations considering the asymptotic behavior of strongly convective and diffusive regimes. We perform numerical simulations of different scenarios for the electroremediation using the Galerkin finite element method together with a staggered algorithm and the Newton–Raphson method. We validate the accuracy of the proposed algorithm by comparing the discrete solutions to the analytical ones. Finally, we explore and discuss optimal scenarios for the electroremediation process depending on the input values of pH, electrical current, and mass inflow using dimensionless numbers defined from the analytical solutions.

Appendix: A Weak Formulation Linearized

The variational model given by (46), (47) and (48) is now linearized by Newton–Raphson method. To this end, we introduce the nonlinear objective functions $F(C^n_{\mathrm{Na}_\mathrm{b}^+})$, $F(C^n_\mathrm{{H}_\mathrm{b}^+})$ e $F(\phi ^n)$, given by

$$\begin{aligned}&F\left( C^n_{\mathrm{Na}_\mathrm{b}^+}\right) := \left( J_{\mathrm{Na}^{+},n}^\mathrm{{eff}},\dfrac{d q_1}{{\text{ d }}x}\right) _{{\varOmega }} - C^n_{\mathrm{Na}_\mathrm{b}^+} V^{n}_\mathrm{{D}}\, q_1\bigg |_{x=L} + C_\mathrm{{Na}}^\mathrm{{res}} \, V^{n}_\mathrm{{D}}\, q_1 \bigg |_{x=0} , \end{aligned}$$

(52)

$$\begin{aligned}&F\left( C^n_\mathrm{{H}_\mathrm{b}^+}\right) := \left( \hat{J}_\mathrm{{H}^{+},n}^\mathrm{{eff}},\dfrac{d q_2}{{\text{ d }}x}\right) _{{\varOmega }} , \quad \quad F(\phi ^n) := \left( I_{f,n}^\mathrm{{eff}},\dfrac{d q_3}{{\text{ d }}x}\right) _{{\varOmega }} + I_0\, q_3\bigg |_{x=0}. \end{aligned}$$

(53)

Defining ${\varUpsilon }^n := \{C^n_{\mathrm{Na}_\mathrm{b}}, C^n_\mathrm{{H}_\mathrm{b}}, \phi ^n\}$ the triple unknown of the system (46)–(48) and the function $F({\varUpsilon }^n) := F(C^n_{\mathrm{Na}_\mathrm{b}}, C^n_\mathrm{{H}_\mathrm{b}}, \phi ^n)$, denoting k the Newton–Raphson method iteration index and expanding $F({\varUpsilon }^n)$ in Taylor series around to the point ${\varUpsilon }^{k,n}$ near the root we have

$$\begin{aligned} F({\varUpsilon }^{k+1,n}) = F({\varUpsilon }^{k,n}) + F'({\varUpsilon }^{k,n})\left( {\varUpsilon }^{k+1,n} - {\varUpsilon }^{k,n}\right) + F''({\varUpsilon }^{k,n})\dfrac{\left( {\varUpsilon }^{k+1,n} - {\varUpsilon }^{k,n}\right) ^2}{2}+\cdots \end{aligned}$$

Imposing the condition $F({\varUpsilon }^{k+1,n}) = 0$, and neglecting the second order terms, we obtain the expression of Newton–Raphson method:

$$\begin{aligned} {\varUpsilon }^{k+1,n} = {\varUpsilon }^{k,n} - \left[ F'({\varUpsilon }^{k,n})\right] ^{-1} F({\varUpsilon }^{k,n}) , \end{aligned}$$

(54)

where $F'({\varUpsilon }^{k,n})$ is the jacobian of the objective function.

The Eq. (54) is used recursively from an initial estimate ${\varUpsilon }^{0,n}$ to the problem root to obtain a sequence values of ${\varUpsilon }^{k+1,n}$ that approximate the nonlinear problem solution. The stopping criterion of the iterative process consists of defining a acceptable value for tolerance $\varepsilon$, so that

$$\begin{aligned} \left| {\varDelta }{\varUpsilon }^{k+1,n}\right| = \left| {\varUpsilon }^{k+1,n} - {\varUpsilon }^{k,n}\right| < \varepsilon . \end{aligned}$$