1 Introduction

The modelling of convective instability in porous layers now has a very strong heritage. The foundational works are by Lapwood (1948) and Horton and Rogers (1945), and these determined the criterion for the onset of convective instability in a horizontal porous layer which is heated from below. In addition, the upper and lower boundaries were considered to be impermeable and subject to constant fixed temperatures, and the porous medium was isotropic and homogeneous. Other types of boundary condition, such as a constant heat flux or constant pressure, may be applied in a variety of different ways; Table 6.1 in Nield and Bejan (2013) gives a comprehensive account of the critical values of the Rayleigh number and wavenumber for these different combinations. The effects of confinement, such as convection in a cuboidal cavity and in a cylindrical cavity (with a circular horizontal planform), were considered by Beck (1972) and Bau and Torrance (1981), respectively. Unlike the corresponding pure fluid configurations, there exist aspect ratios of the cuboid and radii of the cylinder for which the critical Darcy–Rayleigh number is identical with that of the infinite unconfined layer.

The literature is now replete with the study of how the onset and subsequent development of convection is altered by the presence of different effects, such as Brinkman effects, non-Boussinesq effects, the presence of imperfections such as sinusoidally varying boundary temperatures, throughflow effects, rotation, layering, anisotropy, internal heating, local thermal nonequilibrium, more than one diffusing species and unsteady basic states; note that this list, while long, is not comprehensive. Although some work has been reported on configurations where two porous sublayers are separated by a solid intermediate sublayer (see Postelnicu 1999; Jang and Tsai 1988; Patil and Rees 2014; Straughan 2014 for systems of this general type), we are presently interested three-layer systems where a porous sublayer is bounded by two heat-conducting but impermeable solid sublayers.

Mojtabi and Rees (2011) considered such a three-layer system subject to constant heat flux boundary conditions, and this was motivated by the need to model an experimental system where solid boundaries do not have zero thickness and idealised boundary conditions cannot be applied in practice. It was found that the critical parameters (namely the Darcy–Rayleigh number and wavenumber) and the shape of the neutral curve depend quite strongly on the thickness of the solid boundaries and their conductivity relative to that of the porous sublayer. For example, when the solid sublayers are sufficiently highly conducting, the full system may be made to resemble a single porous layer system with constant temperature boundary conditions. In addition, there is a locus in parameter space where the neutral curve has a quartic minimum at zero wavenumber, and this locus separates the regime within which the more usual parabolic minimum at nonzero wavenumbers exists from that where the parabolic minimum is at zero wavenumber. A second study was undertaken by Rees and Mojtabi (2011) where constant temperature boundary conditions were applied. There are many qualitative similarities between this study and the previous one by the same authors except that there is no quartic minimum, and the zero critical wavenumber limit is obtained as the solid conductivities tend to zero. Rees and Mojtabi (2011) also provided a weakly nonlinear analysis to determine regimes within which postcritical convection takes the form of rolls or patterns with square planform; this was an extension of the work of Riahi (1983) who considered solid layers of infinite thickness. A paper by Rees and Mojtabi (2013) also considered the effect on the onset of convection of a horizontal pressure gradient. If was found that there is a thermal drag caused by the stationary solid boundaries which reduces the velocity of the cells along the layer.

In the present paper, we consider the linear stability of a configuration which has some similarities to those of Mojtabi and Rees (2011) and Rees and Mojtabi (2011). Here, the lower solid sublayer is insulated on its lower surface, but its interior is subject to a uniform rate of heat generation, while the upper sublayer is subject to a constant temperature. It is shown in the Appendix that this may be mapped onto a system where the lower solid sublayer is subject to a constant heat flux but without heat generation within the sublayer. While this may seem to be a simple intermediate case between those of Mojtabi and Rees (2011) and Rees and Mojtabi (2011), three different limiting cases for the critical parameters are found in different asymptotic regions of parameter space, and this is a novel finding.

2 Governing Equations and Basic Solution

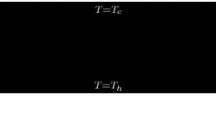
We consider a three-layer system as shown in Fig. 1. It consists of a central uniform porous layer (layer 2) within which convective flow may occur, and this is embedded between two thermally conducting but impermeable layers. These solid layers have identical properties, namely thickness, conductivity and heat capacity. A uniformly cold temperature is imposed on the upper surface of the upper solid layer (layer 3), while the lower layer (layer 1) is subject to uniform Joule heating but its lower surface is insulated. Thus, all the heat is generated within the lowest sublayer and passes out through the upper surface, and a potentially unstable temperature gradient is formed. The origin of the coordinate system is located at the bottom of the porous layer with \({\hat{x}}\) being the horizontal coordinate and \({\hat{z}}\) the vertical coordinate.

Fig. 1
figure 1

Definition sketch of the configuration being studied. The porous layer is sandwiched between two impermeable but thermally conducting layers

Full size image

The full set of governing equations are as follows. For layer 1 (\(-h\le {\hat{z}} \le 0\)):

$$\begin{aligned} (\rho C)_{\mathrm{s}} { \displaystyle \frac{\partial {T_1}}{\partial {{\hat{t}}}}} = {k_{\mathrm{s}}}\left( { \displaystyle \frac{\partial ^2{T_1}}{\partial {{\hat{x}}}^2}} + { \displaystyle \frac{\partial ^2{T_1}}{\partial {{\hat{z}}}^2}} \right) + q; \end{aligned}$$
(1)

for the porous layer (\(0\le z\le H\)):

$$\begin{aligned}&\displaystyle { \displaystyle \frac{\partial {{\hat{u}}}}{\partial {{\hat{x}}}}} + { \displaystyle \frac{\partial {{\hat{w}}}}{\partial {{\hat{z}}}}} = 0, \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle {\hat{u}} = - \frac{K}{\mu } { \displaystyle \frac{\partial {{\hat{p}}}}{\partial {{\hat{x}}}}} , \quad {\hat{w}} = - \frac{K}{\mu } { \displaystyle \frac{\partial {{\hat{p}}}}{\partial {{\hat{z}}}}} + \frac{\rho _{\mathrm{f}} {{\bar{g}}} \beta K}{\mu }(T_2-T_{\mathrm{ref}}), \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle (\rho C)_{\mathrm{pm}} { \displaystyle \frac{\partial {T_2}}{\partial {{\hat{t}}}}} + (\rho C)_{\mathrm{f}} \Bigl (u { \displaystyle \frac{\partial {T_2}}{\partial {{\hat{x}}}}} + w { \displaystyle \frac{\partial {T_2}}{\partial {{\hat{z}}}}} \Bigr ) = {k_{\mathrm{pm}}}\left( { \displaystyle \frac{\partial ^2{T_2}}{\partial {{\hat{x}}}^2}} + { \displaystyle \frac{\partial ^2{T_2}}{\partial {{\hat{z}}}^2}} \right) ; \end{aligned}$$
(4)

and for the upper layer (\(H\le z \le H+h\)):

$$\begin{aligned} (\rho C)_{\mathrm{s}} { \displaystyle \frac{\partial {T_3}}{\partial {{\hat{t}}}}} = {k_{\mathrm{s}}}\left( { \displaystyle \frac{\partial ^2{T_3}}{\partial {{\hat{x}}}^2}} + { \displaystyle \frac{\partial ^2{T_3}}{\partial {{\hat{z}}}^2}} \right) . \end{aligned}$$
(5)

In these equations, the numerical subscripts refer to the appropriate sublayer, and \(T_{\mathrm{ref}}\) is the basic temperature of the interface between the porous sublayer and the lower solid sublayer for the purely conducting situation. The boundary and interface conditions are given by,

$$\begin{aligned} \begin{array}{ll} &{}{\hat{z}} = -h: \quad \displaystyle { \displaystyle \frac{\partial {T_1}}{\partial {z}}} = 0, \\ &{}{\hat{z}} = 0: \quad {\hat{w}}=0, \displaystyle \quad T_1=T_2, \quad {k_{\mathrm{s}}} { \displaystyle \frac{\partial {T_1}}{\partial {{\hat{z}}}}} = {k_{\mathrm{pm}}} { \displaystyle \frac{\partial {T_2}}{\partial {{\hat{z}}}}} , \\ &{}{\hat{z}} = H: \quad {\hat{w}}=0, \displaystyle \quad T_2=T_3, \quad {k_{\mathrm{pm}}} { \displaystyle \frac{\partial {T_2}}{\partial {{\hat{z}}}}} = {k_{\mathrm{s}}} { \displaystyle \frac{\partial {T_3}}{\partial {{\hat{z}}}}} , \\ &{}{\hat{z}} = H+h: \quad T_3 = T_{\mathrm{upper}}. \\ \end{array} \end{aligned}$$
(6)

The basic state consists of no flow (\({\hat{u}}={\hat{w}}=0\)) and a steady \({\hat{z}}\)-dependent temperature. It is a straightforward if tedious matter to determine the conduction profiles in each layer:

$$\begin{aligned} \begin{array}{lr} T_1 = T_{\mathrm{upper}} + \displaystyle q\Bigl [ \frac{3h^2}{2{k_{\mathrm{s}}}} + \frac{Hh}{{k_{\mathrm{pm}}}} \Bigr ] - \frac{q}{{k_{\mathrm{s}}}}\frac{({\hat{z}}+h)^2}{2}, &{} \\ \\ T_2 = T_{\mathrm{upper}} + \displaystyle q\Bigl [ \frac{h^2}{{k_{\mathrm{s}}}} \Bigr ] - \frac{qh}{{k_{\mathrm{pm}}}}({\hat{z}}-H), \\ \\ T_3 = T_{\mathrm{upper}} - \displaystyle \frac{qh}{{k_{\mathrm{s}}}}({\hat{z}}-H-h). \\ \end{array} \end{aligned}$$
(7)

The temperature drop across the porous layer will be used as the temperature scale for the purposes of nondimensionalisation. This value is

$$\begin{aligned} \Delta T = \frac{qHh}{{k_{\mathrm{pm}}}}, \end{aligned}$$
(8)

and we see that the temperature, \(T_{\mathrm{ref}}\), of the lower interface temperature is given by,

$$\begin{aligned} T_{\mathrm{ref}} = T_{\mathrm{upper}} + q\Bigl [ \displaystyle \frac{h^2}{{k_{\mathrm{s}}}} + \frac{Hh}{{k_{\mathrm{pm}}}} \Bigr ]. \end{aligned}$$
(9)

We may now nondimensionalise by introducing the following scalings,

$$\begin{aligned} ({\hat{x}},{\hat{z}})= & {} H(x,z), \quad {\hat{t}}= \frac{H^2}{{k_{\mathrm{pm}}}/(\rho C)_\mathrm{pm}} t, \quad ({\hat{u}},{\hat{w}})=\frac{{k_{\mathrm{pm}}}}{(\rho C)_{\mathrm{f}} H}(u,w), \quad {\hat{p}} = \frac{\mu {k_{\mathrm{pm}}}}{K (\rho C)_{\mathrm{f}}}p, \nonumber \\ T= & {} T_\mathrm{ref} + \Delta T\, \theta . \end{aligned}$$
(10)

Thus, Eqs. (2) and (3) become,

$$\begin{aligned} { \displaystyle \frac{\partial {u}}{\partial {x}}} + { \displaystyle \frac{\partial {w}}{\partial {z}}} =0, \end{aligned}$$
(11)
$$\begin{aligned} u = - { \displaystyle \frac{\partial {p}}{\partial {x}}} , \quad w = - { \displaystyle \frac{\partial {p}}{\partial {z}}} + { Ra}\,\theta , \end{aligned}$$
(12)

Here, the Darcy–Rayleigh number, \({ Ra}\), is defined as,

$$\begin{aligned} { Ra}= \frac{\rho _{\mathrm{f}}{{\bar{g}}} \beta KH\, \Delta T}{\mu ({k_{\mathrm{pm}}}/(\rho C)_{\mathrm{f}}))}, \end{aligned}$$
(13)

where \(\Delta T\) is given in terms of q in Eq. (8). The three heat transport equations become,

$$\begin{aligned}&\displaystyle { \displaystyle \frac{(\rho C)_{\mathrm{s}}}{{k_{\mathrm{s}}}}} { \displaystyle \frac{ {k_{\mathrm{pm}}}}{(\rho C)_{\mathrm{pm}} }} { \displaystyle \frac{\partial {\theta _1}}{\partial {t}}} = { \displaystyle \frac{\partial ^2{\theta _1}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\theta _1}}{\partial {z}^2}} + \frac{1}{d\delta }, \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle { \displaystyle \frac{\partial {\theta _2}}{\partial {t}}} + u { \displaystyle \frac{\partial {\theta _2}}{\partial {x}}} + w { \displaystyle \frac{\partial {\theta _2}}{\partial {z}}} = { \displaystyle \frac{\partial ^2{\theta _2}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\theta _2}}{\partial {z}^2}} , \end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle { \displaystyle \frac{(\rho C)_{\mathrm{s}}}{{k_{\mathrm{s}}}}} { \displaystyle \frac{ {k_{\mathrm{pm}}}}{(\rho C)_{\mathrm{pm}} }} { \displaystyle \frac{\partial {\theta _3}}{\partial {t}}} = { \displaystyle \frac{\partial ^2{\theta _3}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\theta _3}}{\partial {z}^2}} , \end{aligned}$$
(16)

where

$$\begin{aligned} d = \frac{{k_{\mathrm{s}}}}{{k_{\mathrm{pm}}}} \quad \hbox {and} \quad \delta = \frac{h}{H} \end{aligned}$$
(17)

are the respective conductivity and thickness ratios between the solid and porous sublayers.

The boundary and interface conditions given in Eq. (6) become,

$$\begin{aligned} \begin{array}{ll} &{}z = -\delta : \quad \displaystyle { \displaystyle \frac{\partial {\theta _1}}{\partial {z}}} = 0, \\ &{}z = 0: \quad {\hat{w}}=0, \displaystyle \quad \theta _1=\theta _2, \quad d { \displaystyle \frac{\partial {\theta _1}}{\partial {z}}} = { \displaystyle \frac{\partial {\theta _2}}{\partial {z}}} , \\ &{}z = 1: \quad {\hat{w}}=0, \displaystyle \quad \theta _2=\theta _3, \quad { \displaystyle \frac{\partial {\theta _2}}{\partial {z}}} = d { \displaystyle \frac{\partial {\theta _3}}{\partial {z}}} , \\ &{}z = 1+\delta : \quad \theta _3 = -1- { \displaystyle \frac{\delta }{d}} . \\ \end{array} \end{aligned}$$
(18)

The apparently unusual boundary condition for \(\theta _3\) at \(z=1+\delta \) has been defined in such a way that the temperature field varies between 0 and \(-1\) within the porous layer. Thus, the basic solution is given by

$$\begin{aligned} \theta = \left\{ \begin{array}{ll} - { \displaystyle \frac{z(z+2\delta )}{2d\delta }} &{}\quad (-\delta \le z\le 0),\\ - z &{}\quad (0 \le z\le 1),\\ -1 - { \displaystyle \frac{z-1}{d}} &{}\quad (1 \le z\le 1+\delta ).\\ \end{array}\right. \end{aligned}$$
(19)

While there is a unit change in temperature across the porous layer, the overall temperature drop over the whole system is \(1+3\delta /2d\), and this increases as either the thickness of the solid sublayers increase or their conductivity decreases. Five representative profiles of the basic temperature field are given in Fig. 2 for the case \(\delta =0.5\); profiles for other values of \(\delta \) display the same qualititative features. The insulating condition at \(z=-1-\delta \) is evident because of the zero gradient. By design, the temperature profile in the porous layer is independent of the values of both d and \(\delta \).

Fig. 2
figure 2

Basic state temperature profiles for the cases with \(\delta =0.5\): \(d=0.25, \, 0.5\) (short dashes), \(d=1\) (continuous) and \(d=2,4\) (long dashes)

Full size image

Figure 2 shows that there is little variation in the temperature within the solid sublayers when d is large. This happens quite naturally because of the need to conserve the heat flux across the interface. And then, when d takes small values, there is a very large variation in temperature within the solid sublayers.

3 Perturbation Analysis

The basic state consists of the temperature profiles given in Eq. (19) with no flow. Since Squire’s theorem may be shown easily to apply, i.e. that all three-dimensional disturbances may be decomposed into a sum or integral of two-dimensional ones, we need to consider only two-dimensional disturbances. Therefore, we adopt a streamfunction/temperature formulation using, \(u=-\psi _z\) and \(w=\psi _x\), which guarantees that the equation of continuity, Eq. (11), is satisfied. Although the heat transport equations in the two solid sublayers remain unchanged, Eqs. (12) and (15) take the following forms,

$$\begin{aligned} { \displaystyle \frac{\partial ^2{\psi }}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\psi }}{\partial {z}^2}}= & {} { Ra}\, { \displaystyle \frac{\partial {\theta }}{\partial {x}}} , \end{aligned}$$
(20)
$$\begin{aligned} { \displaystyle \frac{\partial {\theta _2}}{\partial {t}}} + { \displaystyle \frac{\partial {\psi }}{\partial {x}}} { \displaystyle \frac{\partial {\theta _2}}{\partial {z}}} - { \displaystyle \frac{\partial {\psi }}{\partial {z}}} { \displaystyle \frac{\partial {\theta _2}}{\partial {x}}}= & {} { \displaystyle \frac{\partial ^2{\theta _2}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\theta _2}}{\partial {z}^2}} . \end{aligned}$$
(21)

We may now introduce a disturbance of infinitesimally small amplitude using,

$$\begin{aligned} \psi = \psi _{\mathrm{basic}} + \Psi , \quad \theta _j = \theta _{j,\,\mathrm basic} + \Theta _j \,\,\, (j=1,2,3), \end{aligned}$$
(22)

where \(\psi _{\mathrm{basic}}=0\) and the basic temperature fields are given in Eq. (19). On neglecting powers of the disturbances, the linearised stability equations take the form,

$$\begin{aligned}&\displaystyle \left( { \displaystyle \frac{(\rho C)_{\mathrm{s}}}{{k_{\mathrm{s}}}}} { \displaystyle \frac{ {k_{\mathrm{pm}}}}{(\rho C)_\mathrm{pm} }} \right) { \displaystyle \frac{\partial {\Theta _1}}{\partial {t}}} = { \displaystyle \frac{\partial ^2{\Theta _1}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\Theta _1}}{\partial {z}^2}} , \end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle { \displaystyle \frac{\partial ^2{\Psi }}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\Psi }}{\partial {z}^2}} = { Ra} { \displaystyle \frac{\partial {\Theta _2}}{\partial {x}}} , \end{aligned}$$
(24)
$$\begin{aligned}&\displaystyle { \displaystyle \frac{\partial {\Theta _2}}{\partial {t}}} = { \displaystyle \frac{\partial ^2{\Theta _2}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\Theta _2}}{\partial {z}^2}} + { \displaystyle \frac{\partial {\Psi }}{\partial {x}}} , \end{aligned}$$
(25)
$$\begin{aligned}&\displaystyle \left( { \displaystyle \frac{(\rho C)_{\mathrm{s}}}{{k_{\mathrm{s}}}}} { \displaystyle \frac{ {k_{\mathrm{pm}}}}{(\rho C)_\mathrm{pm} }} \right) { \displaystyle \frac{\partial {\Theta _3}}{\partial {t}}} = { \displaystyle \frac{\partial ^2{\Theta _3}}{\partial {x}^2}} + { \displaystyle \frac{\partial ^2{\Theta _3}}{\partial {z}^2}} . \end{aligned}$$
(26)

These equations are to be solved subject to the homogeneous form of the boundary conditions given in (18), with the addition of

$$\begin{aligned} \Psi =0 ~~\hbox {on both }z=0\hbox { and }z=1. \end{aligned}$$
(27)

It may also be shown easily that the principle of exchange of stabilities applies, and therefore, the onset of convection is stationary and the time derivatives in Eqs. (23)–(26) may be neglected. If the domain is of infinite horizontal extent, then we may Fourier-decompose disturbances into independent monochromatic cells. Thus, we set,

$$\begin{aligned} \Psi (x,z,t) \rightarrow i \Psi (z) e^{ikx} + \mathrm{c.c.}, \quad \Theta _j(x,z,t) \rightarrow \Theta _j(z) e^{ikx} + \mathrm{c.c.}, \end{aligned}$$
(28)

where k is the horizontal wavenumber. Equations (23)–(26) reduce to

$$\begin{aligned}&\displaystyle \Theta _1'' - k^2\Theta _1=0, \end{aligned}$$
(29)
$$\begin{aligned}&\displaystyle \Psi '' - k^2\Psi = { Ra}\, k \Theta _2, \end{aligned}$$
(30)
$$\begin{aligned}&\displaystyle \Theta _2'' - k^2\Theta _2 = k \Psi _2, \end{aligned}$$
(31)
$$\begin{aligned}&\displaystyle \Theta _3'' - k^2\Theta _3=0, \end{aligned}$$
(32)

where primes denote derivatives with respect to z.

The equations for \(\Theta _1\) and \(\Theta _3\) may be solved analytically and converted into suitable boundary conditions for \(\Theta _2\) upon application of the interface conditions, as follows. For Layer 1, Eq. (29) has the solution,

$$\begin{aligned} \Theta _1 = E \cosh (kz) + F \sinh (kz). \end{aligned}$$
(33)

The application of the boundary condition, \(\Theta _1'(-\delta )=0\), means that this solution may now be written in the form,

$$\begin{aligned} \Theta _1 = E \Bigl [ \cosh (kz) + \tanh (k\delta ) \sinh (kz)\Bigr ]. \end{aligned}$$
(34)

Application of the interface conditions at \(z=0\), namely that \(\Theta _1=\Theta _2\) and \(d\Theta _1'=\Theta _2'\) allows us to eliminate the arbitrary constant, E, to yield

$$\begin{aligned} \Theta _2'(0) = \Theta _2(0) k d \tanh (k\delta ), \end{aligned}$$
(35)

which is regarded as a boundary condition for \(\Theta _2\) that models perfectly the variation of \(\Theta _1\) in the lower sublayer. A similar analysis for \(\Theta _3\) yields

$$\begin{aligned} \Theta _2'(1) = - \Theta _2(1) k d \coth (k\delta ). \end{aligned}$$
(36)

The linear stability problem has now been reduced to solving Eqs. (30) and (31) subject to the two thermal boundary conditions given in (35) and (36), together with those in Eq. (27).

4 Dispersion Relation

Equations (30) and (31) form a fourth-order homogeneous system, and there are four independent solutions. These may be written in the following form,

$$\begin{aligned}&\displaystyle \Psi = \sqrt{{ Ra}}\Bigr ( A \cosh \lambda z + B \sinh \lambda z + C \cos \sigma z + D \sin \sigma z \Bigr ), \end{aligned}$$
(37)
$$\begin{aligned}&\displaystyle \Theta _2 = A \cosh \lambda z + B \sinh \lambda z - C \cos \sigma z - D \sin \sigma z, \end{aligned}$$
(38)

where A, B, C and D are arbitary constants, and where

$$\begin{aligned} \lambda = \sqrt{k(\sqrt{{ Ra}}+k)}, \quad \sigma = \sqrt{k(\sqrt{{ Ra}}-k)}. \end{aligned}$$
(39)

The Darcy–Rayleigh number is found always to lie above the curve, \({ Ra}=k^2\), and therefore, the value of \(\sigma \) is always purely real.

If we now apply the boundary conditions, (27), (35) and (36), then we obtain the following matrix/vector system for the four arbitrary constants:

$$\begin{aligned} \begin{pmatrix} 1 &{} 0 &{} 1 &{} 0 \\ &{} &{} &{} \\ \cosh \lambda &{} \sinh \lambda &{} \cos \sigma &{} \sin \sigma \\ &{} &{} &{} \\ -2kd\tanh (k\delta ) &{} \lambda &{} 0 &{} -\sigma \\ &{} &{} &{} \\ \lambda \sinh \lambda +\quad &{} \lambda \cosh \lambda +\quad &{} \sigma \sin \sigma -\quad &{} -\lambda \cos \lambda -\quad \\ kd\coth (k\delta )\cosh \lambda &{} kd\coth (k\delta )\sinh \lambda &{} kd\coth (k\delta )\cos \sigma &{} kd\coth (k\delta )\sin \sigma \\ \end{pmatrix} \begin{pmatrix} A \\ \\ B \\ \\ C \\ \\ D \\ \end{pmatrix} = \begin{pmatrix} 0 \\ \\ 0 \\ \\ 0 \\ \\ 0 \\ \end{pmatrix}.\nonumber \\ \end{aligned}$$
(40)

This system has nonzero solutions only when the determinant of the matrix is zero. After some manipulation, we find that this determinantal condition is equivalent to

$$\begin{aligned}&\lambda \sigma \Bigl ( 1 -\cosh \lambda \cos \sigma \Bigr ) - (1+2d^2)k^2\sinh \lambda \sin \sigma \nonumber \\&\quad -kd\Bigl (\tanh k\delta +\coth k\delta \Bigr ) \Bigl (\sigma \sinh \lambda \cos \sigma +\lambda \cosh \lambda \sin \sigma \Bigr ) =0. \end{aligned}$$
(41)

It is impossible to solve this equation analytically to give \({ Ra}\) in terms of k, d and \(\delta \), and therefore, we resort to numerical means. A simple Newton-Raphson may be used easily to determine neutral curves as k varies for fixed values of d and \(\delta \). A slightly more complicated version was also written in order to find critical values, i.e. those values of k and \({ Ra}\) at the lowest point of the neutral curve. The manner in which this was undertaken is precisely as described in Rees and Mojtabi (2011) and Rees and Genç (2011) and is therefore omitted here. The codes were written in quadruple precision in Fortran90 because it was found that this amount of precision was required to obtain accurate computations when d and \(\delta \) take values which are as small as \(10^{-10}\) and as large as \(10^{10}\).

5 Results and Discussion

In what follows there are three sets of critical data which are useful references. For the classical Darcy-Bénard layer, the critical values of the Darcy–Rayleigh number and wavenumber are,

$$\begin{aligned} \hbox {CT/CT:}\quad { Ra}_c=4\pi ^2, \quad k_c=\pi , \end{aligned}$$
(42)
Fig. 3
figure 3

Onset profiles for the streamfunction (lower curves) and the temperature (upper curves) for the wavenumber, \(k=2\): a \(\delta =0.4\) with \(d=0.01\) (dotted), 0.1, 1, 10 and 100; b \(d=5\) with \(\delta =0.01\), 0.03, 0.1, 0.3 and 1

Full size image

where the appelation, CT/CT, refers to the fact that both the upper and lower boundary conditions correspond to a constant temperature. When both surfaces are subject to a constant heat flux, we have

$$\begin{aligned} \hbox {CHF/CHF:}\quad { Ra}_c=12, \quad k_c=0. \end{aligned}$$
(43)

Finally, when either surface is subject to a constant temperature, while the other is subject to a constant heat flux, we have

$$\begin{aligned} \hbox {CT/CHF:}\quad { Ra}_c=27.097\,627\,920, \quad k_c=2.326\,214\,580. \end{aligned}$$
(44)

5.1 Onset Profiles

We begin by showing, in Fig. 3, a selection of onset profiles (\(\Psi ,\Theta )\) so that the effect of variations in the two nondimensional parameters, d and \(\delta \), on those profiles may be seen. In both frames the temperature profile, \(\Theta \), takes positive values, while the streamfunction disturbance profile, \(\Psi \), takes negative values. The profiles have been scaled so that the maximum magnitude is precisely unity for easy comparison. Given our definition of the streamfunction, the values of \(\Psi \) turn out conveniently to be negative when \(\Theta \) is positive. Although we have set \(k=2\) in all cases, the qualitative trends shown in Fig. 3 do not change for different wavenumbers.

Figure 3a shows the effect of variations in d when \(\delta =0.4\). When d takes large values, the solid sublayers are highly conducting and we see therefore that the disturbance temperature is almost perfectly constant; this situation is close to the CT/CT single-layer case mentioned above. At the opposite extreme, \(d\ll 1\), the solid layers are poor conductors, and this gives rise to relatively large variations in \(\Theta \) within the solid regions, as was seen for the basic conduction profiles, and only small variations within the porous sublayer. This is approximately the CHF/CHF case mentioned above. It is also interesting to note that the streamfunction profile hardly varies at all over the whole range of values of d.

Figure 3b shows the effect of changing the depth, \(\delta \), of the solid sublayers. We have chosen a fairly representative value for the conductivity ratio, \(d=5\), and this case shows an interesting transition in the profiles from one which is close to being of CT/CT type when \(\delta \) is large (i.e. thick solid sublayers) to one which is almost indistinguishable from a CT/CHF type when \(\delta \) is small. In such cases, the very thin solid sublayers appear to be yield stability properties and profiles which are identical to cases where the layers are entirely absent. We will see later that this initial hypothesis turns out not to be that straightforward in general, and attention must be paid to the magnitude of \(\delta \) in comparison with that of d.

5.2 Neutral Curves

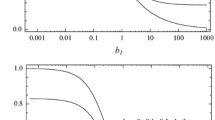
Figure 4 shows a small selection of neutral stability curves for some typical values of the parameters, d and \(\delta \), where each lies in the range, \(10^{-3}\)–\(10^3\). These curves show the standard unimodal form with a clearly identifiable minimum value; numerical investigations indicate that unimodal curves are always obtained for the present configuration. The uppermost curve (\(d=10^3\)) in all four cases is almost exactly identical to that for the classical Darcy-Bénard problem (CT/CT) for which the critical values are \({ Ra}_c=4\pi ^2\) and \(k_c=\pi \). This is because the solid layers are highly conducting which means that temperature variations are rapidly damped, and therefore the interfaces act as perfectly conducting boundary conditions. That said, the critical values for the \(d=10^3\) curve when \(\delta =10^{-3}\) are very slightly smaller than the classical values, but this is difficult to see graphically. On the other hand, the lowest curves (\(d=10^{-3}\)) for all four cases change quite substantially as \(\delta \) increases, and the critical values decrease quite markedly. Indeed, when \(\delta \) is large, the highly insulating bounding layers mimic the CHF/CHF porous layer for which \({ Ra}_c=12\) and \(k=0\).

Fig. 4
figure 4

Neutral curves as a function of k for the indicated values of values of \(\delta \). Curves correspond to \(d=10^{-3}\) (lowest, dotted line), \(10^{-2}\), \(10^{-1}\), \(10^0\), \(10^1\), \(10^2\) and \(10^3\) (uppermost)

Full size image

On the other hand, from these graphs, it is possible to find out how quickly the neutral curves change as d varies. It is clear that there is almost no change in the location of the neutral curve when d increases from \(10^{-2}\) to \(10^2\) when \(\delta =10^{-3}\). But when \(\delta =10^{3}\), there is a rapid change as d increases from \(10^{-1}\) to just below \(10^{1}\); outside of these ranges there is little variation. While we have gleaned this information from Fig. 4, it is clear that we need to consider the variations in the critical parameters themselves, rather than by observing further examples of neutral curves.

Fig. 5
figure 5

Critical values of \({ Ra}\) and k as a function of \(\log _{10}d\) for \(\delta =10^{-6}\), \(10^{-5}\), \(10^{-4}\), \(10^{-3}\), \(10^{-2}\), \(10^{-1}\), \(10^0\) (dotted) and \(10^1\)

Full size image

An extensive set of computations has therefore been undertaken to determine the critical values of \({ Ra}\) and k in the ranges \(10^{-6}\le \delta \le 10^6\) and \(10^{-10}\le d\le 10^{10}\), and these are shown in Fig. 5. Referring to both frames in this figure, we see that the general behaviour of the critical values is that they pass from the CHF/CHF case via the CT/CHF case to the CT/CT case as d increases from exceptionally small values to exceptionally large values. When the solid sublayers are comparable to the thickness of the porous layer, or larger, then there is a direct transition from CHF/CHF to CT/CT which is quite quick near \(d=10^0\) when d is increasing. But when \(\delta < 10^{-3}\), there is range centred on \(d=10^0\) where the composite layer resembles the CT/CHF layer with very high accuracy. Figure 6 shows a close-up image of the central region of the wavenumber curves in Fig. 5. This shows that, when \(\delta =10^{-5}\), the composite layer mimics a CT/CHF single layer when \(10^{-2}<\delta <10^2\), and when \(\delta =10^{-6}\), this happens when \(10^{-3}<\delta <10^3\).

Fig. 6
figure 6

Close-up view of the critical values of k as a function of \(\log _{10}d\) for \(10^{-5}\), \(10^{-4}\), \(10^{-3}\), \(10^{-2}\), \(10^{-1}\), \(10^0\) (dotted) and \(10^1\)

Full size image

In the close-up view, we also see that there is an undershoot in the critical wavenumber as d decreases whenever \(\delta \) is sufficiently small. This presages the passage towards the CT/CHF equivalence. It is unclear what the physical reason for this might be, but a similar behaviour does not occur for the critical Darcy–Rayleigh number.

5.3 Summary

An alternative view of the curves shown in Fig. 5 is provided by Fig. 7, which shows contour representations of both \({ Ra}_c\) and \(k_c\) in the ranges, \(10^{-10}\le d,\delta \le 10^{10}\). A grid with 100 intervals in both directions was used for these figures. We now see clearly how the \((d,\delta )\) plane is divided into three very distinct regions with smooth transitions between these regions. Generally, the right-hand side corresponds to being equivalent to a CT/CT single layer, the left-hand side to a CHF/CHF layer, while the triangular wedge is a CT/CHF configuration. Therefore, our composite layer is clearly capable of supporting three different types of behaviour.

Fig. 7
figure 7

Contours of \({ Ra}_c\) and \(k_c\) as functions of \(\log _{10}d\) and \(\log _{10}\delta \). Integer values of \({ Ra}_c\) are used, while 20 equal intervals between 0 and \(\pi \) are used for \(k_c\). The dotted lines correspond to the CT/CHF case, \({ Ra}_c=27.097628\) and \(k_c=2.326215\)

Full size image

Earlier, a statement was made that what constitutes a narrow solid layer is not a straightforward concept. In Fig. 6, if we choose \(\delta =10^{-5}\) to represent a very thin pair of solid sublayers, then we should expect this to represent the single-layer CT/CHF case simply because \(10^{-5}\) is exceptionally small. However, the critical values correspond to the single-layer CT/CHF critical values only when d lies in the range \(10^{-4}<d<10^4\). Outside of this range, we obtain the CHF/CHF case when \(d<10^{-9}\) and the CT/CT case when \(d>10^5\). These extreme values for d overrule our standard intuition of what ‘thin’ means in the context of the stability. Of course, if one takes the alternative viewpoint that d is fixed, but \(\delta \) decreases, then one will always eventually obtain a CT/CHF configuration.

It is clear from the two subfigures in Fig. 7 that the transitions between the three main regions take place at

$$\begin{aligned} \begin{array}{rl} d\sim 10^0&{} \quad 10^0< \delta , \\ &{} \\ d>10^0:&{} \quad d\delta \sim 1, \\ &{} \\ d<10^0:&{} \quad d\sim \delta .\\ \end{array} \end{aligned}$$
(45)

Finally, Fig. 7 also shows as dotted lines the locus of points which correspond to the CT/CHF critical values given in Eq. (44). While the locus of points for \({ Ra}_c\) forms a straight vertical line which passes downwards through \(d=10^0\), the locus of values of \(k_c\) which satisfies (44) travels in a diagonal direction. However, the values of \(k_c\) which are within the triangular region at the bottom of that contour plot and which are close to \(d=10^0\) are also within \(10^{-6}\) of the CT/CHF value in Eq. (44). This corresponds almost perfectly with the curves given in Fig. 6.

6 Conclusions

We have conducted a linear stability analysis to determine the effect on stability criterion of having two solid but identical bounding sublayers above and below a saturated porous layer where the lower sublayer generates heat internally. The equations were nondimensionlised in such a way that the Darcy–Rayleigh number is based on the temperature drop across the porous layer. There are two parameters, namely the conductivity ratio between the solid and porous sublayers, d and the relative thickness of the bounding plates, \(\delta \). Therefore, we have been able to provide a comprehensive account of the stability properties over a very wide range of values of the parameters. The stability criteria were determined by finding the zeros of a dispersion relation and by minimisation over the wavenumber.

It has been found that the addition of conducting layers above and below the porous layer allows the stability criteria to vary quite substantially and, in particular, to allow this composite layer to mimic one of three standard single-layer configurations, namely the CT/CT, CT/CHF and the CHF/CHF cases. This type of behaviour is quite different from that of Mojtabi and Rees (2011) where the composite layer which they studied only displayed two types of limiting behaviour.

From the practical point of view of constructing an experimental configuration, we have shown that the presence of a physically thin pair of solid bounding plates does not necessarily guarantee that the stability properties correspond to the type (namely CT/CHF) corresponding to the boundary conditions which are applied. Rather, when \(\delta \) is very small, only a certain range of values of d will yield the CT/CHF onset criterion.

We do not know at this stage whether the rolls which we have considered will form the stable mode of convection at values of the Darcy–Rayleigh number which are just above the critical values. Given the conclusions of Riahi (1983) and Rees and Mojtabi (2011), we feel that it is quite likely that square cells are likely to be preferred when the conductivity of the bounding sublayers is sufficiently small, but this aspect would need to be considered quantitatively elsewhere. However, it is very likely indeed that both the roll and square cell patterns will arise from supercritical bifurcations, and therefore, all the results presented here will also be valid should square cells be the preferred pattern post-onset.