1 Introduction

Foam can improve a water flood or a gas drive by decreasing the mobility (phase permeability/apparent viscosity) of the displacing fluids in the reservoir (Bond and Holbrook 1958; Craig and Lummus 1965; Holm 1968). The prediction of foam behavior in porous media relies on proper modeling of the mobility reduction validated by experiments. For the experiments where co-injection of gas and surfactant solution is considered, i.e., pre-generation of foam, one can use the saturation profiles, surfactant concentration profiles, the effluent water cut and the experimental pressure drop for the validation of models (Khatib et al. 1988; Falls et al. 1989; Persoff et al. 1991; Friedmann et al. 1991; Liu et al. 1992; Fergui et al. 1998; Carretero-Carralero et al. 2007; Du et al. 2011). A detailed summary of the literature on foam models can be found in Ma et al. (2014). Most modeling attempts are for experiments with surfactant concentrations well above the critical micelle concentration (CMC) where the buildup of pressure profiles occurs before the injection of about one pore volume. There are only a few experimental data reported in the literature of measured pressure drops with injected concentrations around the CMC, for example by Apaydin and Kovscek (2001). The effluent concentration profile of Suntech IV (an alkyl toluene sulfonate) for Berea sandstone indicates a retardation factor of about 12 for 0.02 w/w % (Huh and Handy 1989). In case of Chaser CD1040 (an alpha olefin sulfonate) with concentrations near the CMC, the steady pressure drop profile is attained after 3–6 pore volumes (PV) in case of Berea sandstones (Chou 1991). To interpret such an observed delay in the pressure drop, one needs models that incorporate the transient development of foam bubbles. Therefore, our interest is in bubble population models by Falls et al. (1988), Ettinger and Radke (1992), Kovscek et al. (1995), Zitha et al. (2006) and Simjoo (2012) that can explain the transient pressure drop at high concentrations as well as at low concentrations, i.e., around CMC.

The bubble population models, mentioned above, combine bubble density balance inside the multiphase flow equations. These multiphase flow equations consist of a water equation, an equation for foam that behaves as a gas with an enhanced viscosity \(\mu _{f}\), a bubble density equation and occasionally a surfactant transport equation. The equations can be solved by using the IMPES method (IMplicit Pressure–Explicit Saturation) described by Aziz and Settari (1979). For simplicity, the flowing bubble density is assumed to be equal to the nonflowing (trapped) bubble density by Kovscek et al. (1995). Therefore, the foam flow in the porous media in case of co-injection of gas and surfactant water can be considered as a flow of two phases, given by the standard Darcy’s law, i.e.,

$$\begin{aligned} u_f = - \frac{kk_{rf}}{\mu _f} (\Delta p_f - \rho _{f} g) , \end{aligned}$$
(1)

where, for foam, \(u_{f}\) is the superficial velocity, k is the absolute permeability, \(k_{rf}\) is the relative permeability, \(\rho _f\) is the density and \(\Delta p_f\) is the observed pressure drop. However, according to Kovscek et al. (1995), \(\mu _f\) is not constant. To estimate the varying viscosity of foam in the two-phase concept, the smallest pores are assumed to be filled with a surfactant solution and other pores with gas bubbles separated by lamellae. A pore level model of foam in porous media consists of bubbles moving in a straight capillary tube (Hirasaki and Lawson 1985). The main resistance of the foam bubble is due to the lamellae that separate the bubble from the pore wall (Bretherton 1961). In addition, the surface tension gradient across the moving bubble contributes significantly to the resistance to foam flow (Hirasaki and Lawson 1985). The added resistance of all bubbles inside the tube can be used to obtain expressions for the apparent foam viscosity. Consequently, the bubble density is an important parameter to estimate the foam viscosity with a fitting parameter \(\alpha \) as given by Kovscek et al. (1995);

$$\begin{aligned} \mu _f = \mu _g + \frac{\alpha ~ n_{f}}{v_{f}^{1/3}}, \end{aligned}$$
(2)

where \(n_{f}\) is the bubble density (number of bubbles per unit distance of the capillary), \(\mu _g\) is the viscosity of unfoamed gas and \(v_f\) is the local interstitial velocity depending on the foamed gas saturation and the fraction of flowing foamed gas.

The bubble density equation, with the apparent viscosity of foam as given above, contains a bubble generation-coalescence function expressed by a source term, \(R(n_{f})\), which is in essence a difference between generation and coalescence rates of bubbles. In most literatures, this source term is based on the assumed foam generation-coalescence mechanisms, e.g., lamellae creation by capillary snap-off, bubble division, bubble coalescence by mass transfer between bubbles (Falls et al. 1988; Rossen 2003). For example, Kovscek et al. (1995) expressed the generation rate with the gas and liquid velocities and the coalescence rate as a function of the bubble density. Similarly, Zitha et al. (2006) proposed a foam generation-coalescence function with an exponential growth of the bubble density for transient foam flow. However, if saturation and flowing fraction of the foam is unknown, an exact bubble generation-coalescence function cannot be directly obtained from the experiments. Therefore, in comparison with previous studies, we propose to determine the bubble generation-coalescence function, i.e., the source term \(R(n_{f})\) approximately from the experimental pressure drop without a priori knowledge of foamed gas saturation and flowing fraction of foam. In our procedure, a first estimate of the bubble density \(n_f\) is obtained from history matching of the experimental pressure drop. Combining Eqs. 1 and 2, we obtain disregarding \(\mu _g\) that

$$\begin{aligned} n_f = \frac{kk_{rf}(\Delta p_f - \rho _f g)}{\alpha ~ u_f} (v_f)^{1/3}. \end{aligned}$$
(3)

As gas saturation and flowing fraction of foam is unknown, it is assumed that foamed gas is the only phase in the porous medium and all foamed gas (foam) is flowing. Therefore, the foam relative permeability, \(k_{rf}\), is equivalent to the permeability, k, and the local interstitial velocity \(v_f\) is equal to \(\frac{u_{f}}{\varphi }\), using that the water saturation is very low. We hypothesize that in such a case, the source term is the derivative of the bubble density, estimated from the experimental pressure drop with respect to time, \(R(n_{f})\approx dn_{f}/dt\). We assume that the viscosity coefficient \(\alpha \) is constant for the case where the adsorption condition is satisfied; i.e., the porous medium is saturated with surfactant, which happens at high concentration. At low concentration (around CMC), we assume that the viscosity coefficient \(\alpha \) varies when the surfactant concentration in the porous medium varies. For such cases, \(\alpha \) is calculated from the surface tension of the injected surfactant concentration derived from the work of Hirasaki and Lawson (1985). We expect that this procedure to estimate \(R(n_{f})\) indeed gives only a first estimate. Once the bubble density is estimated from the experimental pressure drop, the flowing fraction of foam (bubbles) can be estimated by the approximation used by Tang and Kovscek (2006) elaborated in Sect. 3.3. In addition, we calculate the water saturation with the estimated bubble density for a condition of constant foam quality. We assume that the gas saturation remains below the critical gas saturation; therefore, foam does not collapse (Zhou and Rossen 1995). With the saturation and the flowing fraction of foam is known, \(R(n_{f})\), when fully implemented in a flow model should be able to give a simulated pressure drop history that corresponds to the experimental pressure drop history. With the pressure drops comparable to each other, a realistic contribution of the derivative of the bubble density to the source term can be proposed, as described in Sect. 3.8.

To validate our procedure, we carried out foam flow experiments that used co-injection of AOS and \(N_2\) at two concentrations, i.e., at 0.0375 w/w % in double distilled water (CMC) for Bentheimer and at 0.075 w/w % in brine (\(20 \times \hbox { CMC}\)) for the unconsolidated sandpack. We intend to use Bentheimer experiments for a comparison with experiments where nanoparticles were co-injected. The optimal stability of these particles was found at pH 3. Therefore, we choose pH = 3 for the Bentheimer case. Section 2.1 describes the experimental set-up, sample preparation and measurement techniques. In contrast to most literature results, we describe foam flow experiments for a long time (maximum 30 pore volumes) in Sect. 2.2. In addition, we describe in Sect. 2.3 a separate single-phase adsorption test with a Bentheimer core at conditions identical to foam flow experiments to get the adsorption parameters. The main experimental result, shown in Sect. 2.4, is the pressure drop history between two measurement points and the time required to attain a stationary value. Section 3 is about modeling where Sect. 3.1 describes the 1-D model considering downward vertical flow. The balance equations for water-foamed gas and for bubble density with a bubble generation-coalescence function are described in Sect. 3.2. In addition, the pressure equation is used to calculate the simulated pressure drop. In the same Sect. 3.2, two model equations are included for the surfactant adsorption and transport. The procedure to estimate \(R(n_f)\) from the measured pressure drop in terms of the bubble density is explained in Sect. 3.3. The procedure to estimate \(\alpha \), a fitting parameter in the viscosity Eq. 2 from the surfactant concentration, is explained in Sect. 3.4. Boundary conditions are described in Sect. 3.5. We take the case of Bentheimer with the low concentration for the numerical simulation. The model equations from Sect. 3.2 are converted into weak form (Haberman 2004) in Sect. 3.6 to facilitate implementation in COMSOL, a commercial finite element software package. Subsequently, we describe the simulation results (Sect. 3.7) in terms of the water saturation and flowing fraction of foam. In addition, we describe the relation between the bubble density and surfactant concentration for the given simulation. Further, instead of splitting \(R(n_{f})\) like in most studies, we investigate terms on the other side of the bubble density equation, i.e., accumulation, convection and dispersion (diffusion). We determine the relative importance of the bubble accumulation and convection-diffusion terms in Sect. 3.8, where the flowing fraction of foam and the foam saturation is considered. In Sect. 3.9, we compare the experimental pressure drop and the simulated pressure drop for the case of Bentheimer. We end with some conclusions about the procedure used, about the foam generation-coalescence function and about the estimate of the experimental pressure drop.

2 Experimental

2.1 Experimental Set-Up

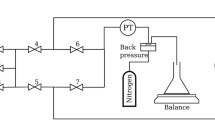
Figure 1 shows the set-up for the foam flow experiments. The set-up consists of an injection module, the core holder containing the sample (24), a production module and measurement equipment. The injection module uses a Pharmacia pump p-900 (12) of the reciprocating type (two cylinders, one for injection and one for refill) with a pumping rate 15–450 ml/h. The injection module further contains a storage glass vessel (13) containing the surfactant solution and a nitrogen gas supply system (1). The storage vessel is connected to the pump by a polymer (nylon) tubing with an inside diameter of 2 mm and an approximate length of 1 m. Nylon tubing with the same diameter connects the pump to a T-junction via valves 3 and 4. Nitrogen gas at a pressure \(7.0\;{\pm }\;0.1\hbox { barA}\) (absolute pressure) is added through valve 3. The core holder contains either a unconsolidated sandpack or a Bentheimer sandstone core. The experiment with the sandpack was conducted with the flow from bottom to top. However, it was easier to do experiments with the flow direction from top to bottom with our set-up. Therefore, we switched the direction for the Bentheimer experiments. We consider the gravity term in the model equations and further in the numerical simulation. The production module consists of a fluid collection vessel (14) to collect the sample and a back pressure valve (17) to control back pressure. Initially, we had visual cell installed in the experimental set-up for the Bentheimer core. However, the pressure drop was very high across the visual cell, which jeopardized an accurate measurement of the pressure drop across the measuring points. For this reason, the visual cell was disconnected. Moreover, the bubble sizes measured in external visual cells may not be representative of in situ texture. An overview of the problems encountered when using a visual cell is described by Ettinger and Radke (1992), Ransohoff and Radke (1988) and Friedmann et al. (1991). The back pressure valve (17) is regulated by high-pressure nitrogen from a cylinder. The outlet of the sandpack/coreholder is connected to nylon tubing with the same internal diameter as the injection tubing, but has a length of 50 cm. There is a flow distributor at the bottom and the top between the injection tube and sandpack to avoid spurious entrance and production effects. At the bottom of the sandpack/coreholder, the flow distributor contains a steel and nylon filter of mesh size 10/cm and a thickness of 0.12 mm to avoid sand spillage. By switching valves (6), (9) and (20), it is possible to change the direction of the flow in the core.

Fig. 1
figure 1

Flow scheme of the set-up used for the foam experiments. The directional signs show the path of the fluids (for example top to bottom of the porous medium). The surfactant solution (13) is mixed with \(\hbox {N}_2\) gas by opening valves (3) and (4) upstream of the unconsolidated sandpack or a Bentheimer core (24). The valves (2–10 and 20) control the flow while manometers (19, 21 and 22) measure the pressures recorded by the computer system (18)

Full size image

2.1.1 Porous Media and Solutions

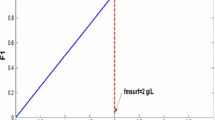
Two different porous media are used in the experiments, viz., an unconsolidated sand of mean size of approximately one mm or Bentheimer cores. The pore size distribution for the unconsolidated sand as shown in Fig. 3 is obtained from image analysis, using an optical microscope. Prior to its use, the sand is treated with a potassium dichromate–sulfuric acid solution to make it completely water-wet. It is kept in the acid for one day and rinsed with tap water until all the acid is removed according to the procedure mentioned by Furniss et al. (1989). Subsequently, the sand is dried and poured, using the procedure of the seven sieves by Wygal (1963), in an acrylic transparent vertical tube to which we refer as the sandpack. The sandpack has an internal diameter of 0.039 m and a length of 0.15 m. The porosity of the unconsolidated sandpack is considered to be 0.38 (Panda and Lake 1994). In case of Bentheimer, the core for the experiment is cut from larger samples and not pretreated prior to its usage. The core is 17 cm in height and 4 cm in diameter and fitted in an aluminum core holder. The porosity of the Bentheimer core is measured to be 0.21 by comparing its weight with and without water, avoiding the presence of air bubbles. The permeability of the sandpack and the core is \(1860\pm 100\) Darcy and for Bentheimer is \(3\pm 0.5\) Darcy, respectively, measured by single-phase (water) test prior to foam flow experiments. We used 39.1 w/w % BIO-TERGE\(^{\textregistered }\) AS-40 sodium \(C_{14-16}\) alpha olefin sulfonate (AOS) to prepare 0.3 w/w % AOS solution in 0.5 M brine and an AOS solution of 0.3 w/w% in acidic (pH = 3) water. We diluted both solutions for the foam experiments to prepare a 0.075 w/w % AOS solution in 0.5 M brine for the unconsolidated sandpack and 0.0375 w/w % AOS in acidic water with dissolved HCl (pH = 3) for Bentheimer. In addition, we measured the surface tension of the given surfactant in DD water in the presence of air with the du Nouy ring tensiometer. The critical micelle concentration of the surfactant decreases with the increase in the salt concentration. In 0.5 M brine, i.e., 30 g of NaCl in 1000 ml water, the critical micelle concentration of AOS is \( 4{\times } 10^{-3} \,\mathrm{wt\%}\) as mentioned by Simjoo et al. (2013). From our surface tension study as shown in Fig. 6, in DD water the critical micelle concentration of AOS is 0.0375 w/w % (1.19 mmol/l). Therefore, the concentrations used for the experiments are \(20 \times \hbox { CMC}\) for the unconsolidated sandpack and CMC for Bentheimer.

2.1.2 Measurement of Pressure, Mass Flow and Temperature

The manometers (19, 21 and 22) and mass balances (15 and 16) are connected to a data acquisition system and a computer (18) to record the pressures and mass flow versus time. The mass flow in (13) and out (14) of the core are determined by weighing the storage vessels on the mass balances (15) and (16), respectively. Figure 2 shows the position of the measurement of the pressure difference across the Bentheimer core and the unconsolidated sandpack. There are four pressure measurement points, viz, at the outlet, inlet and two (for a pressure difference meter) in the middle at a distance of 0.06 m apart for the sandpack and 0.09 m apart for the Bentheimer core. The pressure difference manometer ranges between 0–3 barA (19) with the precision \(\pm 30\hbox { mbarA}\). The pressure difference manometers are calibrated with a pressure calibrator 2095PC (range 1–10 bar). The injection (21) and production side (22) manometers measure absolute pressures in the range 0–65 barA and have a precision of \(\pm 100\hbox { mbarA}\). We did not measure the temperature in the sandpack experiments. In case of the Bentheimer core experiments, a thermocouple (25) is used to measure the temperature at the inlet of the core.

Fig. 2
figure 2

Schematic drawing of the sandpack and Bentheimer core. The foam flow was bottom to top for the unconsolidated sandpack and top to bottom for the Bentheimer core

Full size image
Fig. 3
figure 3

Particle size distribution for the unconsolidated sand. 15 % of the sample particles are below 1 mm, 10 % are above 1.5 mm. Majority of the sample particles are between 1 and 1.5 mm

Full size image

2.2 Flow Experiments

We conducted ten foam flow experiments of which we report two here, i.e., with the unconsolidated sandpack and the Bentheimer sandstone core. As the goal of this paper is to show the procedure of extracting parameters for the bubble generation-coalescence function, we chose only these two experiments for reasons of concise presentation. For the unconsolidated sandpack, the flow is from bottom to top while for the Bentheimer core the flow is from top to the bottom. The foam experiments with unconsolidated sandpack are started at t \(=\) 0 s by flushing surfactant solution with concentrations of 0.075 w/w % AOS (\(20 \times \hbox { CMC}\)) at a rate of \(1.26 \times 10^{-5}\hbox { m/s}\). After one PV of AOS, we achieved a single-phase steady pressure drop of 35,500 Pa/m between the measurement points. At t \(=\) 3309 s from the starting of the experiment, the back pressure valve is opened causing the backpressure to drop from 8.51 to 1.30 barA (absolute pressure). The injection pressure drops from 8.37 to 2.22 barA. At t \(=\) 3346 s (37 s after the release of the back pressure), \(N_{2}\) gas is injected at a rate of \(1.20 \times 10^{-5}\hbox { m/s}\) in the already flowing AOS solution at the T-junction between valve (3) and (4), 30 cm upstream of the sandpack inlet. As the foam develops inside the sandpack, the pressure at the injection point increases leading to compression of gas affecting the ratio of gas to total flow, i.e., foam quality. We calculated this foamed gas velocity or foam velocity (\(u_f\)) by dividing the injection foamed gas velocity with pressure ratio at the injection side. For the experiment with the Bentheimer core, we maintained 4 barA backpressure throughout the experiment. Before the experiment is started, we flushed \({\hbox {CO}}_{2}\) for 5 min followed by 100 ml of water with HCl (pH 3) to remove any trapped gas. The measurements for the foam experiment is started at t \(=\) 0 s by flushing a surfactant solution of 0.0375 w/w % concentration (\(\approx \) CMC) at a rate of \(3.75 \times 10^{-5}\hbox { m/s}\). We waited to achieve a steady liquid pressure drop of 15,300 Pa/m between measuring points. At t \(=\) 3610 s (after 94 ml of AOS solution passed into the core), \(N_{2}\) gas is injected in the already flowing AOS solution at a flow velocity of \(7.8 \times 10^{-5}\hbox { m/s}\). The inlet and outlet pressures at the time of gas injection were 4.22 and 4.18 barA, respectively. After injection of approximately 600 ml of AOS solution with a corresponding amount of gas, the measurements were stopped by closing the gas and liquid flow. The measured temperature fluctuated between 16 and \(17\,^{\circ }\mathrm{C}\). Table 1 summarizes the experiments mentioned above.

2.3 Adsorption Test

For the adsorption test, we maintained conditions identical to the Bentheimer foam experiment, i.e., 0.0375 w/w % AOS in DD water with pH 3 and the same liquid velocity (\(3.6 \times 10^{-5}\hbox { m/s}\)). Before the adsorption test, the permeability of Bentheimer to double distilled water was determined for the flow rates 50–250 ml/h. The calculated permeability was 2.10 Darcy. Potassium iodide (KI), 7 gm, was used as a tracer. From the start of surfactant injection, effluents were collected at the outlet in plastic tubes by fraction collector at various intervals. The effluents were analyzed for total organic carbon (TOC), using a Dhormann 80 apparatus. The potessium iodide tracer was analyzed by the use of ultraviolet–visible Spectrophotometer UV Mini 1240 (Shimadzu).

Table 1 Summary of the foam flow experiments for Sandpack and Bentheimer
Full size table

2.4 Experimental Results

The main result of the foam flow experiments is the pressure drop across the two measurement points in the core. As gravity forces are found negligible (see Sect. 3.6); the increase in pressure drop is due to viscous forces (foam viscosity). Figure 4 shows pressure drop profile obtained from the experiment (triangles) with an unconsolidated sandpack of \(1860\,\pm 100\) Darcy for 10,000 s after the injection gas and AOS solution. The release of the back pressure results in a high flow rate, which subsequently causes a high increase in the pressure drop. We noted the change in the single-phase pressure drop at the injection of gas and consider it as the beginning of the foam generation. Foam generation, represented by the pressure drop, is accelerated due to the already present gas saturation in the sandpack. This is well explained in the models of Ashoori et al. (2011), where an initial gas saturation leads to an accelerating generation of foam. Foam reaches a steady pressure drop value of \(22.0 \times 10^{5}\hbox { Pa/m}\) after injection of 1.3 pore volume at a foam velocity \(1.01 \times 10^{-5}\hbox { m/s}\). The fluctuation in the steady pressure drop is large (\(1.0 \times 10^{4}\hbox { Pa/m}\)) due to gas compression at the inlet of the sandpack leading to change in foam quality. Figure 5 shows results from the experiment (triangles) and from the simulation by COMSOL (2013) (line, discussed in Sect. 3.9) in case of the Bentheimer core for a 0.0375 w/w % AOS solution. In the experiment, the effect of foam generation is observed after 10 pore volumes of gas and water injection. The delay in the pressure drop can be due to two reasons: (1) the low surfactant concentration with a low gas to liquid ratio (0.33), which leads to weak bubbles/lamallae inside the porous medium, and (2) adsorption of the surfactant at the initial stages of the formation of foam.

Fig. 4
figure 4

Experimental pressure drop profile during foam flow in a surfactant-saturated sandpack. Immediate foam formation, as shown in the experimental curve, is due to the high AOS concentration (\(20 \times \hbox { CMC}\))

Full size image
Fig. 5
figure 5

Experimental and simulated pressure drop profile during foam flow in a surfactant-saturated Bentheimer core. The delayed foam formation as shown by the experimental curve is due to the use of low AOS concentration (\(\approx \) CMC)

Full size image

We measured the surface tension (N/m) corresponding to the various values of the surfactant concentration (mmol/l) as shown in Fig. 6. Figure 7 shows the ratio of produced concentration to injected concentration vs the injected pore volume in the Bentheimer core during the adsorption test. The profile with plus sign shows the KI transport. The surfactant transport in the Bentheimer for given conditions (pH 3, 0.0375 w/w% AOS in double distilled water with pH 3) shows time-dependent adsorption. As observed in the literature, for example, by Kuhlman et al. (1992), AOS does not show a Langmuir isotherm and a certain delay in its propagation through the Bentheimer is observed.

Fig. 6
figure 6

Surfactant tension surfactant concentration relation: The CMC for AOS in case of DD water was found at 1.2 mmol/l

Full size image
Fig. 7
figure 7

Adsorption curve: The porous medium is not saturated with the surfactant, even after 14 PV of injection of 0.0375 w/w % AOS

Full size image

3 Modeling

3.1 Physical Model

We consider isothermal foam flow of two phases as proposed by Buckley and Leverett (1942), i.e., a water AOS solution and a high viscosity gaseous phase (foam). We assume that the flow of the foam phase and water phase obeys Darcy’s law for multiphase flow. The total superficial velocity \(u_{t}\), i.e., the sum of the superficial velocities of water and foam phase and the corresponding experimental pressure drops, \(\Delta P_{w}\) and \(\Delta P_{f}\), is expressed as follows,

$$\begin{aligned}&\displaystyle u_{t}=u_{w}+u_{f} \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle u_{t}=-{\frac{kk_{rw}(\Delta {P}_{w}-\rho _{w}g)}{\mu _{w}}-\frac{kk_{rf}(\Delta {P}_{f}-\rho _{f}g)}{\mu _{f}}}. \end{aligned}$$
(5)

We drop the subindexes w and f in the pressure drop \(\Delta P\) (the pressure difference divided by the distance between measuring points), thus ignoring capillary pressure. The foam phase consists of the bubbles bounded by AOS soap films. The resistance to bubble flow in a cylindrical tube can be considered as an apparent viscosity of the foam phase, often expressed as an extrapolation of the Bretherton equation (Bretherton 1961) by Hirasaki and Lawson (1985) and Kovscek et al. (1995), i.e.,

$$\begin{aligned} \mu _{f}=\mu _{g}+\alpha \frac{n_{f}}{v_{f}^{c}} \end{aligned}$$
(6)

where \(\mu _g\) is the gas viscosity, \(n_{f}\) is the bubble density and \(\alpha \) is a fitting parameter for the surfactant effect. Bretherton (1961) used \(c=1/3\) for the exponent. The local interstitial foam velocity \(v_f\) is equal to \(u_f/(\varphi X_f S_g)\), where \(X_f\) is the flowing foam fraction and \(S_g\) is the total saturation of foam. The flowing foam saturation \(S_f\) is related to the total foam saturation by \(S_f=X_f S_g\). The superficial foam velocity depends on the pressure inside the core, i.e., \(u_f= u_\mathrm{{inj}}^\mathrm{{atm}} p_\mathrm{{atm}}/p_\mathrm{{inj}}\), where \(u_\mathrm{{inj}}^\mathrm{{atm}}\) is a foamed gas velocity at the injection point for atmospheric pressure, \(p_\mathrm{{atm}}\). The injection pressure at the inlet of the porous medium is denoted by \(p_\mathrm{{inj}}\). The relative water \(k_{rw}\) and unfoamed gas \(k_{rg}\) permeabilities are given by Brooks and Corey (1966),

$$\begin{aligned} k_{rw}= k_{rw}^{\prime }{S_{we}}^{\frac{2+3\lambda }{\lambda }}, k_{rg}= k_{rg}^{\prime }(1-S_{we})^{2} ({1-S_{we}}^{\frac{2+\lambda }{\lambda }}), \end{aligned}$$
(7)

where \(\lambda \) is pore size distribution index and \(k_{rw}^{\prime }\) (=1) is the permeability to water at the irreducible saturation of gas (\(S_{gr}\)), which we take equal to zero. The permeability to gas at an irreducible water saturation \(S_{wc}\) is \(k_{rg}^{\prime }\) (=1). Moreover, \(S_{we}=(S_{w}-S_{wc})/(1-S_{wc})\) is the effective water saturation, where \(S_w\) is the water saturation. We assume a slightly different relationship than proposed by Kovscek et al. (1995), where the foam relative permeability is a fraction of gas relative permeability connected by the flowing fraction of foam, i.e., \(k_{rf}= X_{f}k_{rg}\).

3.2 Model Equations

We describe foam flow through porous media with four equations: a mass balance equation for the water-foamed gas solution, a pressure equation, a bubble concentration equation and a surfactant transport–adsorption equation. The flow of water with dissolved AOS in the vertical x-direction in the presence of foam is described as a transport equation, viz.(Lake 1989),

$$\begin{aligned} \varphi \partial _{t}{\left( \rho _{w}~S_{w}\right) }-\partial _{x}\left( \rho _{w}~\frac{kk_{rw}}{\mu _{w}}(\partial _{x}{p}-\rho _{w}~g)\right) =\partial _{x}\left( D_{cap}\rho _{w}\partial _{x}S_{w}\right) , \end{aligned}$$
(8)

where \(\rho _{w}\) is the water density, \(k_{w}\) is the water permeability, \(\mu _{w}\) is the water viscosity, \(D_{cap}\) is the capillary diffusion coefficient and p is the pressure. We disregard the saturation dependence of the capillary diffusion coefficient. In order to derive the pressure equation, we assume that the water density \(\rho _{w}\) is pressure dependent. Dividing the equation by \(\rho _{w}\) and rearranging the terms, we obtain

$$\begin{aligned}&\varphi \partial _{t}{\ S_{w}}+\varphi S_{w}\partial _{t}{\ln \rho _{w}} -\partial _{x}\left( \frac{kk_{rw}}{\mu _{w}}(\partial _{x}{p}-\rho _{w}~g)\right) \nonumber \\&\quad -\,\left( \partial _{x}{\ln \rho _{w}}\right) \left( \frac{kk_{rw}}{\mu _{w} }(\partial _{x}{p}-\rho _{w}~g)\right) =\partial _{x}\left( D_\mathrm{{cap}}\partial _{x}S_{w}\right) , \end{aligned}$$
(9)

where we disregard the term involving differentiation toward \(\rho _{w}\) in the diffusion term, i.e., \(\left( \partial _{x}\rho _{w}\right) \left( D_\mathrm{{cap}}\partial _{x}S_{w}\right) \). For the mass balance of foam, we take into account trapped gas. We consider that foam flow through porous media consists of three flow regimes, as described by Ettinger and Radke (1992), i.e., 1. moving liquid 2. foam as a bubble train and 3. trapped bubble train. Therefore, for the given physical model, the trapped foam corresponds to the trapped bubbles and the flowing foam corresponds to the flowing bubbles. The number of trapped bubbles is assumed to be equal to the number of flowing bubbles as in Kovscek et al. (1995); i.e., \(S_{f} n_{f} + S_{t} n_{t}\) becomes \(S_{g} n_{f}\), where \(S_{t}\) is trapped gas saturation, \(n_f\) and \(n_{t}\) are the number of flowing and trapped bubbles per distance of the porous medium, respectively. The relative permeability of the trapped gas is zero. Therefore, the overall mass balance equation for the foamed gas (foam) reads

$$\begin{aligned} \varphi \partial _{t}{(\rho _{f}(p)S_{g})}-\partial _{x}(\rho _{f}(p)\frac{kk_{rf}}{\mu _{f}}(\partial _{x}p-\rho _{f}(p)~g))=\partial _{x}\left( \rho _{f}(p) D_\mathrm{{cap}}\partial _{x}S_{g}\right) , \end{aligned}$$
(10)

where \(\rho _{f}(p)\) is foamed gas density, which depends on the pressure at which the foam is flowing through the porous medium. After expanding the differentiation and dividing by \(\rho _{f}(p)\) we obtain

$$\begin{aligned}&\varphi \partial _{t}{\ S_{g}}+\varphi S_{g}\partial _{t}{\ln \rho _{f} (p)}-\partial _{x}\left( \frac{kk_{f}}{\mu _{f}}(\partial _{x}p-\rho _{f}(p)~g)\right) \nonumber \\&\quad -\partial _{x}\left( \ln \rho _{f}(p)\right) \left( \frac{kk_{rf}}{\mu _{f}}(\partial _{x}p-\rho _{f}(p)~g)\right) =\partial _{x}\left( D_\mathrm{{cap}}\partial _{x}S_{g}\right) , \end{aligned}$$
(11)

where we disregard the term, \(\left( \partial _{x}\rho _{f}\right) \left( D_\mathrm{{cap}}\partial _{x}S_{g}\right) \) involving differentiation toward \(\rho _{f}\) in the diffusion term. We introduce \(c_{w}\) and \(c_{f}\) as the compressibilities for water and foamed gas, respectively. Thus, the term \(\partial _{t}{\ln \rho _{f}(p)}=c_{f}\partial _{t}{p}\) and the term \(\partial _{x}{\ln \rho _{f}(p)}=c_{f}\partial _{x}{p}\). Addition of Eqs. (9) and (11) leads to the pressure equation, i.e.,

$$\begin{aligned}&\varphi ~(S_{w}c_{w}\!+\!S_{g}c_{f})\partial _{t}{p}-\partial _{x}\left( \left( \frac{kk_{rw}}{\mu _{w}}\!+\!\frac{kk_{rf}}{\mu _{f}}\right) \partial _{x}p\right) \!+\!\partial _{x}\left( \frac{kk_{rf}}{\mu _{f}}\rho _{f}(p)~g\!+\!\frac{kk_{rw}}{\mu _{w} }\rho _{w}(p)~g)\right) \nonumber \\&\quad -\,c_{w}\partial _{x}\left( {p}\right) \left( \frac{kk_{rw}}{\mu _{w} }(\partial _{x}{p}-\rho _{w}~g)\right) -c_{f}\partial _{x}(p)\left( \frac{kk_{rf}}{\mu _{f}}(\partial _{x}p-\rho _{f}(p)~g)\right) = 0, \end{aligned}$$
(12)

where the capillary diffusion terms cancel.

The flowing bubble density equation considers accumulation of bubbles in the foam phase convected with the flow. It consists of an accumulation term, a convection term, a kinetic bubble generation-coalescence function to be estimated from the experiment and diffusion terms. The bubble density equation is given by

$$\begin{aligned}&\varphi \partial _{t}{(S_{g}n_{f})}-\partial _{x}\left( n_{f}~\frac{kk_{rf}}{\mu _{f}}(\partial _{x}{p}-\rho _{f}(p)~g)\right) -\varphi ~S_{g}R(n_{f})\nonumber \\&\quad = X_f(n)[\partial _{x}\left( \varphi S_{g}D_{n_{f}}\partial _{x}n_{f}\right) +\partial _{x}\left( D_\mathrm{{cap}}n_{f}\partial _{x}S_{g}\right) ], \end{aligned}$$
(13)

where \(R(n_{f})\) is a source term, which will be estimated by a procedure that uses the Hirasaki–Lawson equation. \(D_{n_{f}}\) and \(D_\mathrm{{cap}}\) are the bubble diffusion and capillary diffusion terms, where diffusion of flowing fraction of foam bubbles is considered.

The model equations for the convection, adsorption and diffusion model (CDA) of the surfactant transport are taken from Trogus et al. (1977) as

$$\begin{aligned}&\displaystyle \partial _{t}C+\frac{u_{w}}{\varphi }\partial _{x}C+\frac{A_{s}}{\varphi }\partial _{t}C_{s}=D_s\frac{\partial ^{2}C}{\partial {{x}^{2}}} \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle \partial _{t}C_{s}=K_{a}(Q_{s}-C_{s})C-K_{d}C_{s}, \end{aligned}$$
(15)

where C is the surfactant concentration in the water, \(C_s\) is the adsorbed surface concentration, \(A_s\) is the rock interstitial area per unit volume (total volume), \(Q_s\) is the total adsorption capacity of the adsorbent, \(K_a\) is the rate of adsorption, \(K_d\) is the rate of desorption and \(D_s\) is the surfactant diffusion coefficient. We assume that the surfactant concentration in the lamellae and the injected water is the same.

3.3 Rough Estimation of Bubble Density, \(n_{f}\), and the Source Term, \(R\left( n_{f}\right) \)

For the estimation of the bubble density, we follow in essence the bubble population approach adopted by Kovscek et al. (1995) for multiphase flow.

Darcy’s law for the foam velocity during multiphase flow reads

$$\begin{aligned} u_{f}=-\left( \frac{kk_{rf}}{\mu _{f}}(\partial _{x}p-\rho _{f}(p)~g)\right) =-\left( \frac{kk_{rf}~ v_{f}^{1/3}}{\alpha ~ n_{f}}(\partial _{x}p-\rho _{f}(p)~g)\right) , \end{aligned}$$
(16)

where we substituted the foam viscosity from Eq. 6. Hence, we obtain

$$\begin{aligned} \partial _{x}p=-\frac{\alpha ~ n_{f}}{v_{f}^{1/3}} \frac{u_{f}}{kk_{rf}}, \end{aligned}$$
(17)

where we disregarded the gravity effect, \(\rho _{f}\left( p\right) g\).

Integration of Eq. (17) between the measurement points, \(x_L\) and \(x_R\), leads to an expression for the pressure drop, i.e.,

$$\begin{aligned} \int _{x_{L}}^{x_{R}} \partial _{x}p~{d}x=-\int _{x_{L}}^{x_{R}} \frac{\alpha ~ n_{f}~ u_{f} }{ v_{f}^{1/3}~ kk_{rf}}{d}x. \end{aligned}$$
(18)

Here \(x_L\) and \(x_R\) denote the left and right position of the pressure difference measurement points, respectively. Initially we consider only single phase flow. As the saturation and flowing fraction of foam is unknown, we assume that foaming gas is the only phase in the porous medium and all the foamed gas is flowing. Therefore, the foam relative permeability is assumed to be equivalent to the bulk permeability, \({ KK}_{rf}=k\). As the water saturation is assumed very low, the local interstitial velocity is equal to the interstitial velocity, i.e., \(v_f=\frac{u_f}{\varphi ~S_g}\approx \frac{u_f}{\varphi }\). We assume that the quantities on the right side of Eq. 18 can be approximated by their average value between the two measurement points, i.e.,

$$\begin{aligned} \frac{p\left( x_{R}\right) -p\left( x_{L}\right) }{x_R-x_L} =-\frac{\alpha ~ n_{f, av}~ u_{f,av} }{v_{f,av}^{1/3}~k_{av}}. \end{aligned}$$

We get the bubble density (ignoring the negative sign for flow) in terms of experimental pressure drop as

$$\begin{aligned} n_{f,av}(t) = \frac{k_{av}~v_{f,av}^{1/3}}{\alpha ~u_{f,av}} \frac{p\left( x_{L}\right) -p\left( x_{R}\right) }{x_R-x_L}. \end{aligned}$$
(19)

As the saturations and flowing fraction of foam are unknown, we determine part of the bubble generation-coalescence function, i.e., the source term \(R(n_{f})\) in Eq. 13 from the experimental pressure drop in terms of the estimated bubble density as

$$\begin{aligned} R({n_{f,av}}) \approx \frac{d{n_{f,av}}}{dt}. \end{aligned}$$
(20)

Figures 8 and 9 show bubble density (\(n_{f,av}\)) versus the derivative of bubble density over time (\(d{n_{av}}/dt\)) in case of an unconsolidated sandpack and Bentheimer. The derivative \(dn_{f,av}/dt\) is calculated as the slope of the line that joins fifty \(n_{f,av}(t)\) values to the corresponding \(t=50\) s with the LINEST function from Microsoft Excel. The interval 50 s was considered optimal in avoiding spurious scattering (for short times) and loosing details (for long times). A fitted linear regression of \(dn_{f,av}/dt\) versus \(n_{f,av}\) is used for fitting unconsolidated sandpack experiment while for fitting Bentheimer experiments, exponential form of \(dn_{f,av}/dt\) versus n was used. The fitted curves are shown in the figures as lines.

Fig. 8
figure 8

Bubble density (\(n_f\)) versus first estimate of the source term \(R(n_f)\): the rate of change of bubble density over time (\(d{n_{f,av}}/dt:=dndt\)) for the unconsolidated sandpack. It is assumed that foamed gas is the only phase in porous medium and all foamed gas is flowing, i.e., \(S_g=1\) and \(X_f =1\)

Full size image
Fig. 9
figure 9

Bubble density (\(n_f\)) vs first estimate of the source term \(R(n_f)\): the rate of change of bubble density over time (\(d{n_{f,av}}/dt:=dndt\)) for Bentheimer core. It is assumed that foamed gas is the only phase in porous medium and all foamed gas is flowing, i.e., \(S_g=1\) and \(X_f =1\)

Full size image

3.4 Estimation of Viscosity Coefficient \(\alpha \) from Surfactant Concentration

The apparent foam viscosity due to the shape (\(\frac{r_c}{R}\)) of the bubble in a cylindrical tube is given by Hirasaki and Lawson (1985) as

$$\begin{aligned} {\mu }^\mathrm{{shape}}_\mathrm{{app}} =0.85 \frac{(\mu _{w} n_L R)}{\left( \frac{r_c}{R}\right) }\left( \frac{3 \mu _{w} U}{ \sigma }\right) ^{-1/3}\left[ \left( \frac{r_{c}}{R}\right) ^2 +1\right] , \end{aligned}$$
(21)

where \(\mu _w\) is the water viscosity, R is the capillary radius, \(r_c\) is the radius of curvature of lamella and \(\sigma \) is the surface tension between surfactant water and gas. This equation can be considered similar to Eq. 6 of viscosity as

$$\begin{aligned} {\mu }^\mathrm{{shape}}_\mathrm{{app}} = \frac{\alpha _\mathrm{{shape}}~n_f}{v_{f}^{1/3}}, \end{aligned}$$
(22)

where \(n_L=n_f\), i.e., the lamellae density is equal to the bubble density and \(U = v_{f}\), i.e., the gas velocity in the capillary tube from Eq. 21 is equal to the local interstitial foam velocity in Eq. 6. The resistance to flow due to the shape of the bubble can be accounted for by the parameter \(\alpha _\mathrm{{shape}}\) as

$$\begin{aligned} \alpha _\mathrm{{shape}} =0.85\frac{\mu _{w} R}{\left( \frac{r_c}{R}\right) }\left( \frac{3 \mu _{w}}{ \sigma }\right) ^{-1/3}\left[ \left( \frac{r_{c}}{R}\right) ^2 +1\right] . \end{aligned}$$
(23)

We assume that the radius of curvature of the lamella is equal to the capillary radius, i.e., \(r_c= R\). Therefore, Eq. 23 simplifies as,

$$\begin{aligned} \alpha _\mathrm{{shape}} =1.18 R~\mu _{w}^{2/3}~\sigma ^{1/3}. \end{aligned}$$
(24)

From Hirasaki and Lawson (1985), the resistance of surface tension gradient to bubble flow in the capillary tube is 10 times higher than the resistance due to the shape of the bubble. Therefore, the total resistance can be considered as a sum given by,

$$\begin{aligned} \alpha = \alpha _\mathrm{\mathrm{{shape}}} + 10 \alpha _\mathrm{{shape}}. \end{aligned}$$
(25)

Therefore, \(\alpha \) varies when the surfactant concentration in the porous medium varies at low concentration (around CMC). The viscosity coefficient \(\alpha \) can be assumed constant for the case where the adsorption condition is satisfied; i.e., the porous medium is saturated with surfactant, which happens at high concentration.

3.5 Boundary Conditions

Here we define boundary conditions based on experiments to be used in the simulations.

Bubble density: The bubble density boundary condition at the injection point \(x=0\) is given by

$$\begin{aligned} n_{f}(x=0,t)=n_\mathrm{{init}} + (n_\mathrm{{inj}}-n_\mathrm{{init}})~r(t), \end{aligned}$$
(26)

where \(n_\mathrm{{init}}\) is the initial bubble density and \(n_\mathrm{{inj}}\) is the bubble density at the point where the bubble–water mixture enters in the core. The bubble density is estimated from Eq. 3 by replacing \(\Delta p_{f}- \rho _{f}g\) with \(\Delta p_{w}- \rho _{w}g\), assuming that the initial pressure drop observed for the two-phase flow is equal to the pressure drop obtained for single-phase water flow. The ramp function r(t), used to avoid discontinuous initial conditions, is zero for \(t \le 0\) and one for \(t \ge 1\). It increases linearly with time in the transition region. For simplicity, we considered \(n_\mathrm{{init}}= n_\mathrm{{inj}}\) in all the cases of our simulations. At the production point \(x=\mathcal {L}\), the derivative of the bubble density is given by

$$\begin{aligned} \partial _{x}{n_{f}(x=\mathcal {L}, {t})}=0 . \end{aligned}$$
(27)

Aqueous phase saturation: In the literature, the flowing fraction of foamed gas during transient flow is considered constant, e.g., by Falls et al. (1988), Zitha et al. (2006) or varying, e.g., by Apaydin and Kovscek (2001) and Tang and Kovscek (2006). In order to estimate the aqueous phase saturation, we consider the flowing fraction of foam to be dependent on the bubble density with the relation \(X_{f}=(\frac{n_{f}}{n_\mathrm{{inj}}})^{-0.4}\), modified from Tang and Kovscek (2006) with the injection bubble density, \(n_\mathrm{{inj}}\) to make the flowing fraction dimensionless. The bubble density at the injection side is given by \({n_{f}}\) and is equal to \({n_{f,\mathrm{{avg}}}}\) estimated in the previous Sect. 3.3. At the injection side \(x=0\), the water phase saturation can be inferred from the foam quality \(\eta \), i.e.,

$$\begin{aligned} \eta = \frac{u_{f}}{u_{w}+u_{f}} . \end{aligned}$$
(28)

The water saturation boundary condition at the injection side can be derived by eliminating the pressure drop from Darcy’s law

$$\begin{aligned} {u}_{w}= & {} -\frac{kk_{rw}}{\mu _{w}}\left( \nabla p \pm \rho _{w}g\right) ,\nonumber \\ {u}_{f}= & {} -\frac{kk_{rf}}{\alpha ~{n_{f}} }{\left( \nabla p \pm \rho _{f}g\right) }{\left( \frac{{u}_{f}}{\varphi S_{g} X_{f}}\right) ^{-1/3}} , \end{aligned}$$
(29)

where the minus sign in \(\pm \) is for the flow from the top to the bottom and the plus sign is for the flow from the bottom to the top. The foam injection velocity is given by the mass injection velocity of nitrogen multiplied by the density and is equal to the injection velocity \({u}_\mathrm{{inj}}^\mathrm{{atm}}\) at atmospheric pressure in \(m/\hbox {s}\). Eliminating the pressure drop from the water equation in Eq. 29 with \(\nabla p=\mu _{w}u_{w}/\left( kk_{rw}\right) \pm \rho _{w}g\), we obtain

$$\begin{aligned} {u}_\mathrm{{inj}}^\mathrm{{atm}}\frac{p_\mathrm{{atm}}}{p_\mathrm{{inj}}} =-\frac{kk_{rf}}{\alpha {n_{f}}}\left( \frac{\varphi S_{g} X_{f}}{{u}_\mathrm{{inj}}^\mathrm{{atm}}\frac{p_\mathrm{{atm}}}{p_\mathrm{{inj}}}}\right) ^{1/3}\left( \frac{\mu _{w}{u}_{w} }{kk_{rw}}\pm \left( \rho _{w}-\rho _{f}\right) g\right) , \end{aligned}$$
(30)

where \({p_\mathrm{{inj}}}\) is the pressure at the injection point. This equation is solved to find the saturation at the injection point. Figure 10 shows the resultant water saturation \(s_\mathrm{{bound}}\) as a function of bubble density for both cases of sandpack and Bentheimer. The water saturation varies from the initial (\(S_\mathrm{{init}}\)) to the final water saturation (\(S_\mathrm{{bound}}\)) and has Dirichet boundary condition \(S_\mathrm{{init}} +(S_\mathrm{{bound}}-S_\mathrm{{init}})~r(t)\), where the ramp function is initially used to avoid a discontinuous saturation at the injection side. The simulation is improved by assuming a smooth initial saturation, concentration and bubble density curve (tangent hyperbolic function). A nonzero water compressibility \(c_{w}\) is required to avoid incompressible flow at the initial condition because \(S_{w} = 1\) and \(S_{g} = 0\). At the production point, \(x=\mathcal {L}\) we specify the derivative of the saturation to be zero (Danckwerts 1953), i.e., \(\partial _{x}{S}_{w}=0\). Once the water saturation and flowing fraction of foam are known, the other saturations are calculated accordingly, i.e., \(S_g = 1-S_w\) and \(S_f=X_{f}~S_g\).

Fig. 10
figure 10

\(S_\mathrm{{bound}}\) estimated from the bubble density for the sandpack (prism) and the Bentheimer case (triangle) considering constant foam quality. The flowing fraction of foam is considered as a function of the estimated bubble density

Full size image

Surfactant concentration: We applied Dirichet boundary condition at the inlet with the prescribed value of C as \(C_\mathrm{{init}} + (C_\mathrm{{bound}}-C_\mathrm{{init}})r(t)\) where \(C_\mathrm{{init}}\) is initial surfactant concentration and \({C_\mathrm{{bound}}}\) is produced surfactant concentration. \(C= {C_\mathrm{{init}}}\) at \(t=0\) (at the time of gas injection) for all x, \(C={C_\mathrm{{init}}}\) at \(x=0\) for all t, \(C={C_\mathrm{{bound}}}\) at \(x=L\) for all t. During the foam experiment with Bentheimer, 3 PV of surfactant solution was injected before gas co-injection. From the adsorption experiment, the adsorbed surface concentration \(C_s\) after 3 PV of surfactant is \(3 \times 10^{-6}\hbox { mmol/m}^2\) at t \(=\) 0 for all x.

3.6 Numerical Solution

We consider here the Bentheimer experiment with low concentration (\(\approx \) CMC) with varying \(\alpha \). The viscosity coefficient \(\alpha \) is calculated from Eq. 25 with changing surfactant concentration, which itself is estimated from the adsorption test. We used the four 1-D equations from Sect. 3.2 in their weak form (Haberman 2004) along coordinate x, i.e., the water saturation equation (Eq. 8), the pressure equation (Eq. 12), the bubble density equation (Eq. 13) and surfactant transport–adsorption equation (Eq. 15). We implemented the model in the multiphysics module of the commercial finite element software, COMSOL version 5.0. We consider a 1-D geometry, consisting of a single domain with a length of 17 cm for the Bentheimer core. The quadratic Lagrangian elements are used with an element size of 0.00017 m for the Bentheimer core. A time-dependent solver (generalized alpha) is used with a linear predictor and an amplification for high frequency of 0.75 (Jansen et al. 2000). In addition, we split the accumulation term of the bubble density and saturation product Eq. (19) in COMSOL into a sum containing a saturation derivative and a bubble density derivative. The termination technique was based on a prescribed tolerance, i.e., sum of absolute error (for each dependent variable) and relative error with maximum number of iterations 5. The convergence criterion for the solution was to arrive at a solution, which is within the specified tolerance. The step is accepted if the solver’s estimate of the (local) absolute error in the solution committed during a time step is smaller than the sum of absolute and relative error.

We obtain the velocity, pressure, saturation and surfactant concentration at each node point. The foam propagation is simulated for a period of \(t= 10,000\) s with output after each 100 s. Fixed values are used for the gas constant (8.314 J/mole/K), the acceleration due to gravity (\(9.81\hbox { m/s}^{2}\)), the water density (\(1000\hbox { kg/m}^{3}\)), the temperature (\(293\hbox { K}\)), the molar weight of nitrogen (\(0.028\hbox { kg/mole}\)). The gas compressibility \(c_{f}\) for ideal gas is 1 / p. The water compressibility is chosen as \(4.58 \times 10^{-10}\hbox { Pa}^{-1}\). The density of nitrogen at atmospheric pressure is \(1.15\hbox { kg/m}^{3}\). The gravity term \((\rho _{f}(p)~g)_{av}L\) is about \(0.69\hbox { Pa}\), which is negligible with respect to the measured pressure difference. We assumed the initial value of \(\lambda \) to be 5 for Bentheimer core with complex mineral composition being slightly larger for the medium with a narrow range of pore sizes (Brooks and Corey 1966). The capillary radius is calculated from capillary theory, \(R = \sqrt{\frac{8k}{\varphi }}\). The value of \(\alpha _\mathrm{{shape}}\) in Eq. (24) is obtained from the surface tension corresponding to the surfactant concentration. Maximum adsorption capacity, \(Q_s\,(\hbox {mmol/m}^2)\), is equal to \(Q_\mathrm{{eqd}}/(S_\mathrm{{sap}}M_\mathrm{{ism}})\), where \(Q_\mathrm{{eqd}}\) is equilibrium adsorption density (0.45 mg/g), specific surface area of pores, \(S_\mathrm{{sap}}\) is \(10\hbox { m}^2/\hbox {g}\), and injected surfactant molecular weight, \(M_\mathrm{{ism}}\) is 315 mg/mmol. Weight of the core is taken as \(W_c\) (200 g) and pv is the pore volume. The rock interstitial area, \(A_s\), is calculated by \(S_\mathrm{{sap}} W_c/(pv)\) as \(20\times 10^6\hbox { m}^2/\hbox {m}^3\). We fitted the adsorption curve of the single-phase flow simulation with the adsorption parameters \(k_{a}\) and \(k_{d}\). The parameters used for the simulation are given in Table 2.

Table 2 Parameters used for implementation of the model in the commercial software
Full size table

3.7 Numerical Results

The main output of the foam flow simulation is the pressure drop, water saturation and bubble density. As our primary goal in this work was to relate the bubble generation function to the experimental pressure drop, a detailed convergence analysis as in Ames (1977) for such a nonlinear problem is considered outside the scope of current paper. In case of the Bentheimer core with low concentration, the surfactant concentration along with the surfactant adsorption is compared with the experimental results.

The effect of spatial grid and temporal density on the simulated pressure drop profile is measured. The solution is “mesh convergent” as mesh refinement from 0.00017 to 0.00005 m did not significantly change pressure drop profile. Similarly, the change in prescribed tolerance, i.e., temporal density from \(1 \times 10^{-8}\) to \(1 \times 10^{-6}\) did not change the pressure drop profile. We conducted numerical experiments to study the effect of perturbation of parameters (here taken as constant), i.e., capillary diffusion, \(D_\mathrm{{cap}}\) and bubble diffusion, \(D_{nf}\) on the pressure drop profile. Initially, we selected \(D_\mathrm{{cap}}\), \(1 \times 10^{-8}\hbox { m}^2/\hbox {s}\) and \(D_{nf}\), \(1 \times 10^{-7}\hbox { m}^2/\hbox {s}\). An optimization routine is followed in COMSOL for different values of bubble diffusion and capillary diffusion for a minimization of the difference between experimental and predicted pressure drop. Thus, we arrived at values given in Table 2, which give a simulation result closer to the experimental result. Figures 11 and 12 give a sense of the impact of the possible uncertainties in the pressure profile for the given values of bubble diffusion and capillary diffusion, respectively.

Fig. 11
figure 11

Variation in bubble diffusion (\(\hbox {D}_\mathrm{nf}\)). Capillary diffusion (\(\mathrm{D}_\mathrm{cap}\)) is constant, e.g., \(9.3 \times 10^{-7}\hbox { m}^2/\hbox {s}\)

Full size image
Fig. 12
figure 12

Variation in capillary diffusion (\(\mathrm{D}_\mathrm{cap}\)). Bubble diffusion (\(\hbox {D}_\mathrm{nf}\)) is constant, e.g., \(2.2 \times 10^{-5}\hbox { m}^2/\hbox {s}\)

Full size image

Saturation profile: Figure 13 shows the saturation profile for the simulation for foam flow across the Bentheimer core. Change in the initial condition from a step function to a tanh has a minor but noticeable effect on the results. The curves show the saturation across the length of the core at the indicated times in seconds and in pore volumes (PV) in brackets. The 100 s curve shows that the saturation at the entrance of the Bentheimer is \(\approx 0.62\). As time passes, i.e., 200 s after co-injection of the surfactant solution and gas, the water saturation shows typical front observed in Buckley and Leverett (1942). After 5000 s, the saturation increases, leading to a decrease in the pressure drop. At the end of the simulation (10,000 s), the water saturation is still a decreasing function of the distance from the injection point. Figure 14 shows the flowing fraction of foam. As the time passes, the flowing fraction decreases. The flowing fraction of foam is varying during the transient state and constant at steady state. At the steady state, the flowing fraction is \(\approx 0.12\), which is similar to the values found by Tang and Kovscek (2006).

Fig. 13
figure 13

Numerical saturation profile in the x-direction for Bentheimer case

Full size image
Fig. 14
figure 14

Flowing fraction of foam in the x-direction for Bentheimer case

Full size image

Bubble density profile: Figure 15 shows the simulated bubble density profile along with the corresponding surfactant concentration profile for Bentheimer. As time passes, i.e., 100 s to 1000 s, the bubble density increases from 231 / m at the inlet to a maximum value of 47, 810 / m at the exit of the Bentheimer core. The bubble density continues to increase even though water saturation increases after 5000 s as shown in Fig. 13. The variation in surfactant concentration affects the bubble density via varying viscosity coefficient \(\alpha \) in Eq. 2. The bubble density increase is directly proportional to the surfactant concentration increase in the core. The surfactant concentration (dotted curve) propagates as a moving front (100 s, 200–1000 s). At the end of the simulation, the concentration is not equal everywhere but shows a slight gradient, i.e., \(C_\mathrm{{produced}}/C_\mathrm{{injected}}=0.95\), where \(C_\mathrm{{produced}}\) is the surfactant concentration in the produced solution, while \(C_\mathrm{{injected}}\) is the injected surfactant concentration. Corresponding bubble density is not equal everywhere affecting the calculation of the source term from the experimental pressure drop between the measurement points.

Fig. 15
figure 15

Numerical bubble density and surfactant concentration plot in the x-direction for Bentheimer. The dashed curve is the surfactant concentration, and the drawn curve is the bubble density. There is a nonzero gradient of the bubble density in the domain between the measurement points (4.5 and 13.5 cm), even after long times. This shows the need to use an average bubble density (\(n_{f, av}\)) in Eq. 19

Full size image

3.8 Terms Contributing to the Pressure Drop

Here we determine the relative importance of the terms in the bubble density equation. The bubble density equation Eq. 13 has been modified, replacing the potential gradient terms by the Darcy velocity of the foam, i.e.,

$$\begin{aligned}&\varphi n_f\partial _{t}{S_{g}}+ \varphi S_{g}\partial _{t}{n_f} - \partial _{x}\left( {n_f~u_{f}}\right) \nonumber \\&\qquad - X_f[\partial _{x}\left( \varphi S_{g}D_{n_{f}}\partial _{x}n_{f}\right) +\partial _{x}\left( D_{cap}n_{f}\partial _{x}S_{g}\right) ]\nonumber \\&\quad =\varphi ~S_{g} R(n_f). \end{aligned}$$
(31)

We calculated the terms from Eq. 31 in case of Bentheimer as shown in Fig. 16 averaged over the domain between the measurement points. The gas saturation change over time (\(\varphi ~n_{f}~\partial _{t}{S_g}\)) hardly contributes to the generation-coalescence function throughout the simulation. During transient flow (from 0 till 4200 s, \(\approx 12\hbox { PV}\)), the source term, \(R(n_f)\), is balanced by the bubble density change (\(\varphi ~S_{g}~\partial _{t}{n_f}\)) and the convection-diffusion of bubbles. Our initial estimate, \(R(n_f) \approx \partial _{t}{n_f}\) (Fig. 9), was based on the assumption that gas is the only phase in the porous medium \(S_g=1\) and all gas is flowing as a foam, \(X_f =1\). However, in the simulation we consider two-phase flow (Fig. 13) and there is a varying foamed gas flowing fraction (Fig. 14). Therefore, in addition to bubble density variation over time affected by surfactant concentration (Fig. 15), the source term has a contribution of convection-diffusion terms. After transient flow, when the foam is in apparent steady state, \(\partial _{t}{n}\) is zero, the number of bubbles is constant. During this steady state, the convection and the diffusion mechanisms are observed to be dominant.

Fig. 16
figure 16

Terms contributing to the bubble generation-coalescence function (line with pyramid) in flow simulation for the Bentheimer due to (1) accumulation terms, (a) gas saturation change over time: \(\varphi n_f\partial _{t}{S_{g}}\) (cross), (b) bubble density change over time: \(\varphi S_{g} \partial _{t}{n_f}\) (small square), (2) convection-diffusion terms (plus sign) from Eq. 31. Unlike the first estimate of \(R(n_f)\) in Fig. 9, here we consider two-phase flow (Fig. 13) and flowing foam fraction (Fig. 14)

Full size image

3.9 Comparison Between Experimental and Simulation Results

The simulated pressure profile in case of the Bentheimer experiment in Fig. 5 mimics features observed in the experimental result: the delayed foam generation and decrease in the pressure drop before it reaches steady value of \(2.3\times 10^{6}\hbox { Pa/m}\). The simulation shows that the water saturation increases after the maximum pressure drop is achieved. The increase in water saturation causes a decrease in the pressure drop across the measurement points. However, the bubble density continues to increase in this part of the simulation. After 15 PV of AOS and gas injection, the simulated water saturation achieved a constant value of 0.62, leading to a steady value of the pressure drop \(2.3\times 10^{6}\hbox { Pa/m}\). The mean absolute error between theoretical and experimental pressure drop is \(1.06 \times 10^5\hbox { Pa/m}\), i.e., within 10 % of the experimental pressure drop. Possible reasons for the imperfect match between simulation based on the proposed theoretical procedure and the experimental results are lack of fitting profiles in case of the uncertainty in the estimation of (a) the bubble density \(n_f\) from the experimental pressure drop, (b) the dn/dt from n and (c) the adsorption parameters \(k_{a}, k_{d}\) from the adsorption experiment. In addition, the adsorption parameters are taken from the single-phase experiment where the available surface area for adsorption is less than the surface area for multiphase foam flow. The role of bubble diffusion is not very well understood. These issues could be addressed in future work. In addition, to use the above procedure in the field, a further upscaling step is required, for instance using homogenization (Salimi and Bruining 2011).

4 Conclusions

  • The experimental pressure drop across the measurement points can be used to obtain a first estimate of the average bubble density, which can be further used to obtain part of the source term.

  • We measured the experimental pressure drop for two surfactant concentrations (20 \(\times \) CMC and CMC) and for two permeabilities (1860 and 3 Darcy). For the unconsolidated sandpack experiment (1860 Darcy), the steady state profiles are achieved after 1.3 pore volume (PV) of AOS injection with a concentration 20 \(\times \) CMC. For Bentheimer sandstone (3 Darcy), the steady state pressure drop is achieved after injection of 12–15 pore volume of low concentrations of AOS surfactant (of the order of the critical micelle concentration (CMC)) due to adsorption behavior. The experimental pressure drop shows a weak maximum in the unconsolidated sandpack and a strong maximum in the Bentheimer core.

  • A model that leads to four equations, viz., a pressure equation, a water saturation equation, a bubble density equation and a surfactant transport–adsorption equation can describe the pressure drop during the foam flow experiments. The viscosity coefficient \(\alpha \) in the Hirasaki–Lawson equation is estimated from the surfactant concentration to relate the foam viscosity to the estimated bubble density. The trapped gas fraction and the water saturation can be taken into account as a function of bubble density.

  • For the Bentheimer case, simulations indicate that the maximum in the pressure drop corresponds to a minimum in the water saturation. With the assumption that all gas is foamed and foam is the only phase in the porous medium, it is asserted that the dependence between the source term and bubble density is approximately obtained. The difference between simulated and experimental pressure drop is within 10 %, which suggests that the first estimate of the bubble generation-coalescence function is of the right order of magnitude.

  • Instead of splitting the source term \(R(n_f)\), we investigate terms on the other side of the bubble density equation, i.e., accumulation, convection and dispersion (diffusion). The study gives us an idea about their individual contribution to \(R(n_f)\). As we approximated \(\alpha \) as a resistance per lamella in the capillary tube, the generation-coalescence function can only be obtained within a factor. If we consider water saturation (two-phase flow) and flowing fraction of foam, the rate of change of bubble density during transient state can be equated to the bubble density generation function plus the terms accounted for bubble transport by convection and diffusion divided by porosity and saturation.