Two-Phase Immiscible Flows in Porous Media: The Mesocopic Maxwell–Stefan Approach

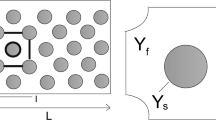
Abstract

We develop an approach to coupling between viscous flows of the two phases in porous media, based on the Maxwell–Stefan formalism. Two versions of the formalism are presented: the general form, and the form based on the interaction of the flowing phases with the interface between them. The last approach is supported by the description of the flow on the mesoscopic level, as coupled boundary problems for the Brinkmann or Stokes equations. It becomes possible, in some simplifying geometric assumptions, to derive exact expressions for the phenomenological coefficients in the Maxwell–Stefan transport equations. Sample computations show, among other, that apparent relative permeabilities are dependent on the viscosity ratio; that the overall mobility of the phases decreases compared to the standard Buckley–Leverett formalism; and that the effect is determined by the parameter determining the “degree of mixing” between the flowing phases. Comparison to the available experimental data on the steady-state two-phase relative permeabilities is presented.

Appendix: Solution of the Brinkmann Problems for the Jet Model

The solutions for the jet model should be obtained for four different cases (cf. Eqs. 29, 30). There are solutions for the outer and for the inner jet. The solutions should be obtained for $s<s^{*}$ and for $s>s^{*}$. If $s<s^{*}$, the outer jet is orange, and the inner jet is white. For the case of $s>s^{*}$, the colors exchange.

We will consider in detail the solution for the outer jet problem and for $s<s^{*}$, so that the phase is orange. Other solutions will be briefly described.

The governing Brinkmann equation is

$$\begin{aligned} P_x =-\frac{\mu _o }{K_o }W_o +\frac{\mu _{eo} }{r}\frac{d}{dr}\left( r\frac{dW_o }{dr}\right) \end{aligned}$$

With the boundary conditions at the inner and outer boundaries of the jet,

$$\begin{aligned} W_o (r_j )=V,\quad \frac{dW_o }{dr}(R)=0 \end{aligned}$$

(37)

These boundary conditions correspond to the case where all the inner jets are active ($I_P =0)$. For the case where some jets are passive, the first boundary condition should be substituted by $W_o (r_j )=0$ for fraction $I_P$ of the jets. This is a particular case of the first condition (37), with $V=0$.

Let us first consider the case with no passive inner jets, $I_P =0$. The effect of passive jets will be added later.

By substitutions

$$\begin{aligned} W_o =U-\frac{K_o }{\mu _o }P_x ; \quad r^{\prime }=r\big /\sqrt{K_o \gamma _o }, \end{aligned}$$

the equation considered is reduced to the zero-order modified Bessel equation as:

$$\begin{aligned} \frac{1}{r^{\prime }}\frac{d}{dr^{\prime }}\left( r^{\prime }\frac{dU}{dr^{\prime }}\right) -U=0 \end{aligned}$$

Solving it and making back-substitution, we express $W_0$ in the general form of

$$\begin{aligned} W_o =-\frac{K_o }{\mu _o }P_x +C_1 {I}_0 \left( r\big /\sqrt{K_o \gamma _o }\right) +C_2 {K}_0 \left( r\big /\sqrt{K_o \gamma _o }\right) \end{aligned}$$

Here, ${I}_0 ,\;{K}_0$ are modified Bessel functions of the first and second kind, $C_i$ are the constants to be determined from the boundary conditions (37). Substitution of the values $r_j ,\;R$ into the solution and resolving with regard to these constants results in

$$\begin{aligned} C_1&= \frac{\hbox {K}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) }{\Delta }\left( V+\frac{K_o }{\mu _o }P_x \right) ;\quad C_2 =\frac{\hbox {I}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) }{\Delta }\left( V+\frac{K_o }{\mu _o }P_x \right) ;\; \\ \Delta&= \hbox {K}_0 \left( r_j \big /\sqrt{K_o \gamma _o }\right) \hbox {I}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) +\hbox {K}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) \hbox {I}_0 \left( r_j \big /\sqrt{K_o \gamma _o }\right) \end{aligned}$$

The first-order Bessel functions arise from the differentiation of the zero-order functions, as required by the second boundary condition (37).

The average velocity $U_o$ is found as (cf. Eq. 21):

$$\begin{aligned} U_o =\frac{\phi }{R^{2}}\int _{r_j }^R {W_o 2rdr} \end{aligned}$$

Substitution of the solution $W_0$ and rather elaborate, but straightforward integration with application of the tabulated integrals of the type of $\int {xI_0 (x)dx,\;\int {xK_0 (x)dx} }$ results in

$$\begin{aligned} U_o&= -\frac{K_o \phi (1-s)}{\mu _o }P_x +L_{oV} \left( \phi (1-s)V+\frac{K_o \phi (1-s)}{\mu _o }P_x \right) \nonumber \\ L_{oV}&= L_{oV} \left( \frac{r_j }{\sqrt{K_o \gamma _o }},\frac{R}{\sqrt{K_o \gamma _o }}\right) =\frac{2\sqrt{K_o \gamma _o }r_j \Delta _1 }{R^{2}(1-s)\Delta };\nonumber \\ \Delta&= \hbox {K}_0 \left( r_j\big /\sqrt{K_o \gamma _o }\right) \hbox {I}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) +\hbox {K}_1 \left( R\big /\sqrt{K_o \gamma _o }\right) \hbox {I}_0 \left( r_j \big /\sqrt{K_o \gamma _o }\right) \nonumber \\ \Delta _1&= \hbox {I}_1 \left( \frac{R}{\sqrt{K_o \gamma _o }}\right) \hbox {K}_1 \left( \frac{r_j }{\sqrt{K_o \gamma _o }}\right) -\hbox {K}_1 \left( \frac{R}{\sqrt{K_o \gamma _o }}\right) \hbox {I}_1 \left( \frac{r_j }{\sqrt{K_o \gamma _o }}\right) \end{aligned}$$

(38)

This expression is equivalent to the first expression (29), with account of Eq. (26). It may be shown by manipulation with the Bessel functions that

$$\begin{aligned} \frac{\partial \Delta }{\partial r_j }=-\frac{\Delta _1 }{\sqrt{K_o \gamma _o }};\quad \Delta _1 =-\sqrt{K_o \gamma _o }\frac{\partial \Delta }{\partial r_j } \end{aligned}$$

Thus, the expression for coefficient $L_{oV}$ has the form of

$$\begin{aligned} L_{oV} =L_{oV} \left( \frac{r_j }{\sqrt{K_o \gamma _o }},\frac{R}{\sqrt{K_o \gamma _o }}\right) =-\frac{2K_o \gamma _o r_j }{R^{2}(1-s)\Delta }\frac{\partial \Delta }{\partial r_j }=-\frac{2K_o \gamma _o }{R^{2}(1-s)}\frac{\partial \ln \Delta }{\partial \ln r_j } \end{aligned}$$

Equation (38) has the form similar to Eq. (25). Comparison shows that for the case of no passive jets, $L_{oV} =l_{oV}$. This proves the first of Eq. (29).

We have considered the case where all the inner jets are active $(I_P =0)$. If, on the contrary, all the inner jets would be passive $(I_P =1)$, the solution would be given by Eq. (38) with $V=0$. The complete solution is the linear combination of the solutions with active and with passive inner jets

$$\begin{aligned} U_o&= (1-I_P )\left[ -\frac{K_o \phi (1-s)}{\mu _o }P_x +L_{oV} \left( \phi (1-s)V+\frac{K_o \phi (1-s)}{\mu _o }P_x \right) \right] \\&+\,I_P \left[ -(1-L_{oV} )\frac{K_o \phi (1-s)}{\mu _o }P_x \right] \end{aligned}$$

Comparison with Eq. (25) results in

$$\begin{aligned} k_o&= \frac{1-L_{oV} }{1-(1-I_P )L_{oV} }K_o \phi (1-s)\\ l_{oV}&= (1-I_P )L_{oV} \end{aligned}$$

The first equation provides the connection between the meso- and macroscale permeabilities for oil. It is not used for computations in the present work, but may be important for experimental studies. The second equation is the result mentioned at the end of Sect. 4.2.

The flow in the active inner part of the jet at $s<s^{*}$ is described by the Brinkmann Eq. (27) with boundary conditions (28). Averaging is performed as above. The passive jets form the fraction of the volume where the flow velocity is zero. The resulting expression for the flow velocity is

$$\begin{aligned} U_w =-(1-I_P )\frac{K_w \phi s}{\mu _w }P_x +(1-I_P )L_{wV} \left( \phi sV+\frac{K_w \phi s}{\mu _w }P_x \right) , \end{aligned}$$

where $L_{wV}$ is given by the formula equivalent to the second Eq. (29)

$$\begin{aligned} L_{wV} =\frac{2r_j \sqrt{K_w \gamma _w }}{sR^{2}}\hbox {I}_1 \left( \frac{r_j }{\sqrt{K_w \gamma _w }}\right) \Big /\hbox {I}_0 \left( \frac{r_j }{\sqrt{K_w \gamma _w }}\right) \end{aligned}$$

Comparison with Eq. (25) recovers equations

$$\begin{aligned} k_w&= \frac{(1-I_P )(1-L_{wV} )}{1-(1-I_P )L_{wV} }K_w \phi s;\\ l_{wV}&= (1-I_P )L_{wV} \end{aligned}$$

The case of $s>s^{*}$ is considered in a similar way.