Abstract
A simple mathematical theory is proposed to investigate the development of the flow field which is the response of a fluid to the buoyancy force due to the existence of a temperature gradient in a hemispherical fluid-saturated porous medium, assuming the validity of the Brinkman model. The induced flow is assumed to be slow, and Stokes approximation is invoked. It is shown, at all times, the induced fluid motion occurs in the form of eddies on either side of the axis of symmetry. In the steady state, the behavior of the fluid motion on the free surface is similar to that of axial fluid flow.






Similar content being viewed by others

Abbreviations
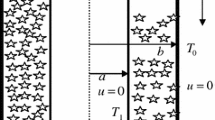
- \(a\) :
-
Radius of the hemisphere [L]
- \(c_{\mathrm{p}}\) :
-
Specific heat at constant pressure [\(\hbox {L}^{2}\,\hbox {T}^{2}\,\Omega ^{-1}\)]
- \(D_{\mathrm{a}}\) :
-
Darcy number, \(Ka^{-2}\)
- \(\hbox {e}_{n}\) :
-
Coefficients in the series expansion (Eq. 12)
- \(f\) :
-
Function of \(\varphi \) (Eq. 12)
- \(f_{n}\) :
- \(G_{n}\) :
-
Gegenbauer polynomial of order \(n\) (Eq .15)
- \(g\) :
-
Acceleration due to gravity
- \(J_{m}\) :
-
Bessel functions of the first kind of odd order \(m\)
- \(K\) :
-
Permeability of the porous medium [\(\hbox {L}^{2}\)]
- n :
-
Unit vector along the \(\varphi = 0\) axis
- Pr :
-
Prandtl number, \(\nu /\alpha \)
- \(P\) :
-
Fluid pressure in excess of its hydrostatic value [\(\hbox {L M}^{-1}\,\hbox {T}^{2}\)]
- \(P_{n}\) :
-
Legendre polynomial of order n of the first kind
- q :
-
Fluid velocity \((u, v, w)\) [\(\hbox {L T}^{-1}\)]
- \(R\) :
-
Non-dimensional radial co-ordinate
- \(R_{\mathrm{a}}\) :
-
Thermal Rayleigh number \((\beta {gKa}/\alpha \nu )\hbox {T}_{0}\)
- \(r\) :
-
Radial co-ordinate [L]
- \(T\) :
-
Temperature [\(\Omega \)]
- \(T_{0}\) :
-
Temperature of the free surface [\(\Omega \)]
- \(t\) :
-
Time [T]
- \(U\) :
-
Non-dimensional radial component of velocity
- \(U_\mathrm{ax}\) :
-
Steady-state axial velocity
- \(u\) :
-
Radial component of velocity [\(\hbox {L T}^{-1}\)]
- \(V\) :
-
Non-dimensional transverse component of velocity
- \(\nu \) :
-
Transverse component of velocity [\(\hbox {L T}^{-1}\)]
- \(\alpha \) :
-
Effective thermal diffusivity of the fluid-porous matrix [\(\hbox {L}^{2}\,\hbox {T}^{-1}\)]
- \(\beta \) :
-
Thermal expansion coefficient [\(\Omega ^{-1}\)]
- \(\lambda \) :
-
Square root of the reciprocal of the Darcy number
- \(\varepsilon \) :
-
Porosity of the porous medium [\(\hbox {ML}^{-1}\Omega \)]
- \(\theta \) :
-
Azimuthal angle
- \(\varphi \) :
-
Meridian angle
- \(\eta _{k}\) :
-
\(k\)th positive zero of \(J_{2n+3/2}(\eta )\)
- \(\zeta \) :
-
\(\hbox {cos}\varphi \)
- \(\mu \) :
-
Coefficient of viscosity of the fluid [\(\hbox {ML}^{-1}\,\hbox {T}^{-1}\)]
- \(\mu ^*\) :
-
Effective viscosity in the porous medium [\(\hbox {ML}^{-1}\hbox {T}^{-1}\)]
- \(\nu \) :
-
Kinematic viscosity of the fluid [\(\hbox {L}^{2}\hbox {T}^{-1}\)]
- \(\nu ^*\) :
-
Effective kinematic viscosity of the fluid in the medium [\(\hbox {L}^{2}\hbox {T}^{-1}\)]
- \(\rho \) :
-
Fluid density [\(\hbox {ML}^{-3}\)]
- \(\rho _{0}\) :
-
Fluid density when the temperature is \(\hbox {T}_{0}\,[\hbox {ML}^{-3}]\)
- \(\psi \) :
-
Stream function [\(\hbox {L}^{3}\hbox {T}^{-1}\)]
- \(\varPsi \) :
-
Non-dimensional stream function
- \(\varPsi _{0}\) :
-
First convective correction to the flow field
- \(\sigma \) :
-
Heat capacity ratio, \(\varepsilon + (1- \varepsilon )(\rho \hbox {c}_{\mathrm{p}})_{s}/(\rho \hbox {c}_{\mathrm{p}})_{f}\)
- \(\omega \) :
-
\(\lambda (\hbox {s} + 1)^{1/2}\)
- \(\chi _{n}\) :
-
Function of \((R,s)\) (Eq. 18)
- \(\tau \) :
-
Non-dimensional time
- \(\varTheta \) :
-
Non-dimensional temperature
- \(\varTheta _{0}\) :
-
Conduction state solution for the temperature distribution
- \(\varPhi _{n}\) :
-
Laplace transform of \(\varPsi _{n}(R,\tau )\)
- \(\varpi \) :
-
Absolute difference between the temperature at the deepest point of the hemisphere and the free surface
- \({\nabla }\) :
-
The gradient vector
- \({\nabla }^{2}\) :
-
The Laplacian operator
- \(n\) :
-
\(n\)th term
- f:
-
Fluid phase
- s:
-
Solid phase
References
Baytas, A.C., Grisan, T., Pop, I.: Free convection in spherical annular sectors filled with a porous medium. Transp. Porous Media 49, 191–207 (2002)
Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34 (1949)
Burns, P.J., Tien, C.L.: Natural convection in porous media bounded by concentric spheres and horizontal cylinders. Int. J. Heat Mass Transf. 22, 929–939 (1979)
Charrier-Mojtabi, M.C., Mojtabi, A.: Natural convection in a horizontal porous annulus. In: Ingham, D.B., Pop, I. (eds.) Transport Phenomena in Porous Media, chap. VII, pp. 155–178. Pergamon Press, Oxford (1998)
Cheng, P.: Advances in Heat Transfer, vol. 14. Academic Press, New York (1978)
Datta, A.K.: Porous media approaches to studying simultaneous heat and mass transfer in food processes. I: problem formulations. J. Food Eng. 80, 80–95 (2007)
Ganapathy, R.: Thermal convection from an instantaneous point heat source in a porous medium. Int. J. Eng. Sci. 28(9), 907–918 (1990)
Hinch, E.J.: An averaged equation approach to particle interaction in a fluid suspension. J. Fluid Mech. 83(4), 695–720 (1977)
Howells, I.D.: Drag due to the motion of a Newtonian fluid through a sparse random array of small fixed rigid objects. J. Fluid Mech. 64, 449–485 (1974)
Joseph, D.D., Tao, L.N.: The effect of permeability on the slow motion of a porous sphere in a viscous liquid. Z. Angew. Math. Mech. 44(8–9), 361–364 (1974)
Koplik, J., Levine, H., Zee, A.: Viscosity re-normalization in the Brinkman equation. Phys. Fluids 26(10), 2864–2870 (1983)
Lundgren, T.S.: Slow flow through stationary random beds and suspension of spheres. J. Fluid Mech. 51(2), 273–294 (1972)
Mack, L.R., Hardee, H.C.: Natural convection between concentric spheres at low Rayleigh numbers. Int. J. Heat Mass Transf. 11, 387–396 (1968)
Neale, G., Epstein, N., Nader, W.: Creeping flow relative to permeable spheres. Chem. Eng. Sci. 28(10), 1865–1874 (1973). Erratum: 29, 1352 (1974)
Nield, D.A., Bejan, A.: Convection in Porous Media, 4th edn. Springer, New York (2013)
Ooms, G., Mijnlief, P.F., Beckers, H.L.: Frictional force exerted by a flowing fluid on a permeable particle with particular reference to polymer coils. J. Chem. Phys. 53, 4123–4130 (1970)
Tam, C.K.W.: The drag on a cloud of spherical particles in low Reynolds number flow. J. Fluid Mech. 38(3), 537–546 (1969)
Acknowledgments
The author is thankful to the referees for their many useful suggestions which led to a definite improvement of the paper. The support of the Principal, MAM College of Engineering (Anna University), Tiruchirapalli is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ganapathy, R. Thermal Convection in a Non-darcy Hemispherical Porous Medium. Transp Porous Med 105, 105–115 (2014). https://doi.org/10.1007/s11242-014-0362-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-014-0362-z