Elastic Waves in Swelling Porous Media

Abstract

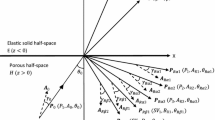
Time harmonic waves in a swelling porous elastic medium of infinite extent and consisting of solid, liquid and gas phases have been studied. Employing Eringen’s theory of swelling porous media, it has been shown that there exist three dilatational and two shear waves propagating with distinct velocities. The velocities of these waves are found to be frequency dependent and complex valued, showing that the waves are attenuating in nature. Here, the appearance of an additional shear wave is new and arises due to swelling phenomena of the medium, which disappears in the absence of swelling. The reflection phenomenon of an incident dilatational wave from a stress-free plane boundary of a porous elastic half-space has been investigated for two types of boundary surfaces: (i) surface having open pores and (ii) surface having sealed pores. Using appropriate boundary conditions for these boundary surfaces, the equations giving the reflection coefficients corresponding to various reflected waves are presented. Numerical computations are performed for a specific model consisting of sandstone, water and carbon dioxide as solid, liquid and gas phases, respectively, of the porous medium. The variations of phase speeds and their corresponding attenuation coefficients are depicted against frequency parameter for all the existing waves. The variations of reflection coefficients and corresponding energy ratios against the angle of incidence are also computed and depicted graphically. It has been shown that in a limiting case, Eringen’s theory of swelling porous media reduces to Tuncay and Corapcioglu theory of porous media containing two immiscible fluids. The various numerical results under these two theories have been compared graphically.

Appendices

Appendix 1

The explicit expressions of the elements of matrices $P$ and $Q$ are given as

$$\begin{aligned} p_{1i}&= L_ik_{\alpha i}^2-2{\bar{a}}_{11}k^2,\quad p_{1J}=2{\bar{a}}_{11}kd_{\beta j},\quad p_{2i}=M_ik_{\alpha i}^2-2f_i{\bar{a}}_{22}k^2,\\ p_{2J}&= 2{\bar{f}}_j{\bar{a}}_{22}kd_{\beta j},\quad p_{3i}=N_ik_{\alpha i}^2,\quad p_{3J}=0,\quad p_{4i}=2kd_{\alpha i},\\ p_{4J}&= 2k^2-k_{\beta j}^2,\quad p_{5i}=f_ip_{4i},\quad p_{5J}={\bar{f}}_{j}p_{4J},\quad q_i=-p_{i1},\quad q_J=p_{J1},\\ L_i&= a_{11}+f_ia_{12}+g_ia_{13},\quad M_i=a_{12}+f_ia_{22}+g_ia_{23},\quad N_i=a_{13}+f_ia_{23}+g_ia_{33}, \end{aligned}$$

where $i=1,2,3;\quad j=1,2;\quad J = j+3.$

Appendix 2

The explicit expressions of the elements of matrices $P^{\prime }$ and $Q^{\prime }$ are given as

$$\begin{aligned} p_{1i}^{\prime }&= (L_i+M_i+N_i)k_{\alpha i}^2-2({\bar{a}}_{11}+f_{i}{\bar{a}}_{22})k^2,\quad p^{\prime }_{1J}=2({\bar{a}}_{11}+{\bar{f}}_j{\bar{a}}_{22})kd_{\beta j},\\ p_{2i}^{\prime }&= 2({\bar{a}}_{11}+f_i{\bar{a}}_{22})kd_{\alpha i},\quad p^{\prime }_{2J}=({\bar{a}}_{11}+{\bar{f}}_j{\bar{a}}_{22})(2k^2-k_{\beta j}^2),\quad p^{\prime }_{3i}=(1-f_i)k,\\ p_{3J}^{\prime }&= -(1-{\bar{f}}_j)d_{\beta j},\quad p^{\prime }_{4i}=(1-f_i)d_{\alpha i},\quad p^{\prime }_{4J}=(1-{\bar{f}}_j)k,\quad p^{\prime }_{5i}=(1-g_i)d_{\alpha i},\\ p_{5J}^{\prime }&= (1-{\bar{g}}_j)k,\quad q^{\prime }_1=-p^{\prime }_{11},\quad q^{\prime }_2=p^{\prime }_{21},\quad q^{\prime }_3=-p^{\prime }_{31},\quad q^{\prime }_J=p^{\prime }_{J1},\\ L_i&= a_{11}+f_ia_{12}+g_ia_{13},\quad M_i=a_{12}+f_ia_{22}+g_ia_{23},\quad N_i=a_{13}+f_ia_{23}+g_ia_{33}, \end{aligned}$$

where $i=1,2,3;\quad j=1,2;\quad J = j+3.$

Appendix 3

The explicit expressions of the elements of the matrix $F$ are given by

$$\begin{aligned} F_{0i}&= -D_1\big [\big (L_1+f_i^*M_1+g_i^*N_1 \big )k_{\alpha 1}^2d_{\alpha i}^*-2k\big ({\bar{a}}_{11}+f_1f_i^*{\bar{a}}_{22}\big ) \big (kd_{\alpha i}^*+k^*d_{\alpha 1}\big )\big ],\\ F_{0J}&= -D_1\big [\big (L_1+{\bar{f}}_j^*M_1+{\bar{g}}_j^*N_1 \big )k_{\alpha 1}^2k^*-2k\big ({\bar{a}}_{11}+f_1{\bar{f}}_j^*{\bar{a}}_{22}\big )\big (kk^*-d_{\beta j}^*d_{\alpha 1}\big )\big ],\\ F_{i0}&= D_1\big [\big (L_i+f_1^*M_i+g_1^*N_i \big )k_{\alpha i}^2k^*-2k\big ({\bar{a}}_{11}+f_if_1^*{\bar{a}}_{22}\big )\big (kd_{\alpha 1}^*+k^*d_{\alpha i}\big )\big ],\\ F_{ij}&= -D_1\big [\big (L_i+f_j^*M_i+g_j^*N_i \big )k_{\alpha i}^2d_{\alpha j}^*-2k\big ({\bar{a}}_{11}+f_if_j^*{\bar{a}}_{22}\big )\big (kd_{\alpha j}^*-k^*d_{\alpha i}\big )\big ],\\ F_{i3}&= -D_1\big [\big (L_i+f_3^*M_i+g_3^*N_i \big )k_{\alpha i}^2d_{\alpha 3}^*-2k\big ({\bar{a}}_{11}+f_if_3^*{\bar{a}}_{22}\big ) \big (kd_{\alpha 3}^*-k^*d_{\alpha i}\big )\big ],\\ F_{iJ}&= -D_1\big [\big (L_i+{\bar{f}}_j^*M_i+{\bar{g}}_j^*N_i \big )k_{\alpha i}^2k^*-2k\big ({\bar{a}}_{11}+f_i{\bar{f}}_j^*{\bar{a}}_{22}\big ) \big (kk^*+d_{\beta j}^*d_{\alpha i}\big )\big ],\\ F_{J0}&= D_1\big ({\bar{a}}_{11}+{\bar{f}}_jf^*_1{\bar{a}}_{22}\big ) \big [k_{\beta j}^2k^*-2k\big (kk^*-d_{\alpha 1}^*d_{\beta j}\big )\big ],\\ F_{Ji}&= D_1\big ({\bar{a}}_{11}+{\bar{f}}_jf^*_i{\bar{a}}_{22}\big ) \big [k_{\beta j}^2k^*-2k\big (kk^*+d_{\alpha i}^*d_{\beta j}\big )\big ],\\ F_{4J}&= -D_1\big ({\bar{a}}_{11}+{\bar{f}}_1{\bar{f}}^*_j{\bar{a}}_{22}\big ) \big [k_{\beta 1}^2d_{\beta j}^*-2k\big (kd_{\beta j}^*-k^*d_{\beta 1}\big )\big ],\\ F_{5J}&= -D_1 \big ({\bar{a}}_{11}+{\bar{f}}_2{\bar{f}}^*_j{\bar{a}}_{22}\big ) \big [k_{\beta 2}^2d_{\beta j}^*-2k\big (kd_{\beta j}^*-k^*d_{\beta 2}\big ) \big ],\\ F_{00}&= -F_{11},\quad D_1=\omega |A^2_0|,\\ L_i&= a_{11}+f_ia_{12}+g_ia_{13},\quad M_i=a_{12}+f_ia_{22}+g_ia_{23},\quad N_i=a_{13}+f_ia_{23}+g_ia_{33}, \end{aligned}$$

where $i=1,2,3;\quad j=1,2;\quad J = j+3.$