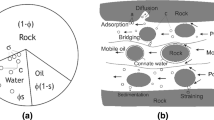
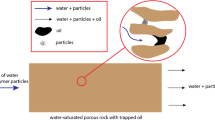
Abstract
A novel concept for modeling pore-scale phenomena included in several enhanced oil recovery (EOR) methods is presented. The approach combines a quasi-static invasion percolation model with a single-phase dynamic transport model in order to integrate mechanistic chemical oil mobilization methods. A framework is proposed that incorporates mobilization of capillary trapped oil. We show how double displacement of reservoir fluids can contribute to mobilize oil that are capillary trapped after waterflooding. In particular, we elaborate how the physics of colloidal dispersion gels (CDG) or linked polymer solutions (LPS) is implemented. The linked polymer solutions consist of low concentration partially hydrolyzed polyacrylamide polymer crosslinked with aluminum citrate. Laboratory core floods have shown demonstrated increased oil recovery by injection of linked polymer solution systems. LPS consist of roughly spherical particles with sizes in the nanometer range (50–150 nm). The LPS process involve mechanisms such as change in rheological properties effect, adsorption and entrapment processes that can lead to a microscopic diversion and mobilization of waterflood trapped oil. The purpose is to model the physical processes occurring on pore scale during injection of linked polymer solutions. A sensitivity study has also been performed on trapped oil saturation with respect to wettability status to analyze the efficiency of LPS on different wettability conditions. The network modeling results suggest that weakly wet reservoirs are more suitable candidates for performing linked polymer solution injection.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Abbreviations
- A :
-
Langmuir adsorption coefficient (cm3/g)
- AP 1,2,3 :
-
Constant coefficients (cm3/g)
- B :
-
Langmuir adsorption coefficient (cm3/g)
- C lg :
-
Critical concentration for log jamming mechanism (g/cm3)
- C p :
-
Polymer concentration (g/cm3)
- C s :
-
Critical concentration for straining mechanism (g/cm3)
- f :
-
Fractional flow rate (–)
- G :
-
Absolute pore element conductance
- G f :
-
Water corner layer conductance
- g pc :
-
Bonds conductance
- G w :
-
Water bulk conductance
- i, j, k:
-
Bonds index (–)
- N ca :
-
Capillary number (–)
- P :
-
Pressure (Pa)
- Q :
-
Bonds flow rate (m3/s)
- q :
-
Flow rate (m3/s)
- R b :
-
Bond radius (μm)
- R p :
-
Polymer effective hydrodynamic radius (μm)
- S :
-
Log-jamming curve increase (–)
- α :
-
Oil-filled fractional in partially filled bond
- μ :
-
Viscosity (Pa.s)
- μ w :
-
Water viscosity (Pa.s)
- σ :
-
Interfacial tension (N/m)
References
Aarra, M.G., Bjørsvik, M., Høiland, H., Skodvin, T., Skauge, A.: Linked polymer solutions for improved oil recovery by waterflooding. In: 13th European Symposium in Improved Oil Recovery. 25–27 April. SPE. Budapest, Hungary (2005)
Al-Gharbi, M.S., Blunt, M.J.: Dynamic network modelling of two-phase drainage in porous media. Phys. Rev. E 71, 016308 (2005)
Avraam D.G., Payatakes A.C.: Flow mechanisms, relative permeabilities and coupling effects in steady-state two-phase flow in porous media. The case of strong wettability. Ind. Eng. Chem. Res. 38, 778–786 (1999)
Berkowits B., Balberg I.: Percolation theory and its application to groundwater hydrology. Water Res. 29, 775–794 (1993)
Bjørsvik, M.: Physico-chemistry characterization of colloidal dispersion gels. PhD thesis, University of Bergen, Norway (2008)
Bjørsvik, M., Høiland, H., Skauge, A.: Formation of colloidal dispersion gels from aqueous polyacrylamide solutions. Colloids Surfaces A (2007). doi:10.1016/j.colsurfa.2007.11.025
Blunt M., King M.J., Scher H.: Simulation and theory of two-phase flow in porous media. Phys. Rev. A 46(12), 7680–7699 (1992)
Blunt M.J., Jackson M.D., Piri M., Valvatne P.H.: Detailed physics, predictive capabilities and macroscopic consequences for pore-network models of multiphase flow. Adv. Water Resour. 25, 1069–1089 (2002)
Bolandtaba, S.F., Skauge, A., Mackay, E.: Pore-scale modeling of linked polymer solution (LPS)—a new EOR process. In: EAGE IOR Conference, Paris, 27–29 April (2009)
Broadbent S.R., Hammersley J.M.: Percolation processes, I and II. Proc. Camb. Philos. Soc. 53, 629–645 (1957)
Chang H.L., Sui X., Xiao L., Guo Z., Yao Y., Xiao Y., Chen G., Song K., Mack J.C.: Successful field pilot of in-depth colloidal dispersion gel (CDG) technology in daqing oil field. SPE Res. Eval. Eng. 9(5), 664–673 (2006)
Chatzis I., Dullien F.A.L.: Modelling pore structures by 2-D and 3-D networks with application to sandstones. J. Can. Petrol. Technol. 16, 97–108 (1977)
Constantinides G.N., Payatakes A.C.: Network simulation of steady-state two-phase flow in consolidated porous media. AIChE J. 42, 369–382 (1996)
Dias M.M., Payatakes A.C.: Network models for two-phase flow in porous media. Part 1. Immiscible microdisplacement of non-wetting fluids. J. Fluid Mech. 164, 305–336 (1986a)
Dias M.M., Payatakes A.C.: Network models for two-phase flow in porous media. Part 2. Motion of oil ganglia. J. Fluid Mech. 164, 337–358 (1986b)
Dias, D., Somaruga, C., Norman, C., Romero, J.: Colloidal dispersion gels improve oil recovery in a heterogeneous Argentina waterflood. SPE 113320-MS-P. In: SPE/DOE Improved Oil Recovery Symposium, Tulsa, Oklahoma, USA, 19–23 April (2008)
Dixit A.B., Mc Dougall S.R., Sorbie K.S., Buckley J.S.: Pore-scale modeling of wettability effects and their influence on oil recovery. SPE Reserv. Eval. Eng. 2, 25–36 (1999)
Dominguez, J.G., Willhite, G.P.: Retention and flow characteristics of polymer solutions in porous media. Soc. Pet. Eng. J. April, 111–121 (1977)
Dong, H., Puhua, Y., Weili, L.Y., Qingxia, L., Shaozi, C., Zhengyu, S., Jinxing, T., Xiaolei.: Flow mechanism investigation and field practice for low concentration flowing gel. In: SPE 50929 SPE International Conference and Exhibition. Beijing, China 2–6 November (1998)
Fatt I.: The network model of porous media. I. Capillary pressure characteristics. Trans. AIME 207, 144–159 (1956a)
Fatt I.: The network model of porous media. II. Dynamic properties of a single size tube network. Trans. AIME 207, 160–163 (1956b)
Fatt I.: The network model of porous media. III. Dynamic properties of networks with tube radius distribution. Trans. AIME 207, 164–181 (1956c)
Fenwick D.H., Blunt M.J.: Network modeling of three-phase flow in porous media. SPE J. 3, 86–97 (1998)
Flory P.J.: Principles of Polymer Chemistry. Cornel University Press, Ithaca (1953)
Gunstensen A.K., Rothman D.H.: Lattice Boltzmann studies of immiscible two-phase flow through porous media. J. Geophys. Res. 98(B4), 6431–6441 (1993)
Heiba A.A., Sahimi M., Scriven L.E., Davis H.T.: Percolation theory of two-phase relative permeability. SPE Reserv. Eng. 7, 123–132 (1992)
Hou J.: Network modeling of residual oil displacement after polymer flooding. J. Pet. Sci. Eng. 59(2007), 321–332 (2007)
Hughes R.G., Blunt M.J.: Pore-scale modeling of multiphase flow in fractures and matrix/fracture transfer. SPE J. 6(21), 26–36 (2001)
Huh, C., Lange, E.A., Cannella, W.J.: Polymer retention in porous media. SPE 20235. In: SPE/DOE Enhanced Oil Recovery Symposium. Tulsa, Oklahoma, USA, 22–25 (1990)
Jerauld G.R., Salter S.J.: Effect of pore-structure on hysteresis in relative permeability and capillary pressure: pore-level modeling. Transp. Porous Media 5, 103–151 (1990)
Joekar-niasar, S.M., Hassanizadeh, H.K., Dahle, H.K.: Non-equilibrium effects in capillarity and interfacial area in two-phase flow: dynamic pore-network modelling. J. Fluid Mech. (2010). doi:10.1017/S0022112010000704
Koplik J., Lasseter T.J.: Two-phase flow in random network models of porous media. Soc. Petrol. Engng. J. 25, 89–100 (1985)
Kovscek A.R., Wong H., Radke C.J.: Scenario for the development of mixed wettability in oil reservoirs. AIChE J. 39(6), 1072–1085 (1993)
Lenormand, R., Zarcone, C.: Role of roughness and edges during imbibition in square capillaries. In: 59th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers of AIME, SPE 13264. Houston, Texas (1984)
Mack, J.C., Smith, J.E.: In-depth colloidal dispersion gels improve oil recovery efficiency. SPE/DOE 27780. In: SPE/DOE 9th Symposium on Improved Recovery. Tulsa, Oklahoma, 17–20 April (1994)
Mogensen K., Stenby E.H.: A dynamic two-phase pore-scale model for imbibition. Transp. Porous Media 32, 299–327 (1998)
Mohanty, K.K., Salter, S.J.: Multiphase flow in porous media pore level modeling. Paper SPE 11018. In: SPE Annual Technical Conference And Exhibition. New Orleans, Louisiana, 26–29 September (1982)
Morrow N.R.: Effects of surface roughness on contact angle with special reference to petroleum recovery. J. Can. Pet. Technol. 14, 42–53 (1975)
Nguyen, V., Sheppard, A, Pinczewski, W, Knackstedt, M.: A dynamic network model for imbibition, Society of Petroleum Engineers International Petroleum Conference, Puebla, Mexico, November 9, SPE Paper Number 90365 (2004)
Øren P.E., Bakke S., Arntzen O.J.: Extending predictive capabilities to network models. SPE J. 3, 324–336 (1998)
Osterloh, W.T., Law, E.J.: Polymer transport and rheological properties for polymer flooding in the North Sea Captain Field. SPE 39694. In: SPE/DOE Enhanced Oil Recovery Symposium, Tulsa, Oklahoma, USA, 19–22 April (1998)
Patzek T.W.: Fundamentals of Multiphase Flow in Porous Media, 1st edn. Berkeley, U.C. Berkeley (1998)
Payatakes A.C.: Dynamics of oil ganglia during immiscible displacement in water-wet porous media. Ann. Rev. Fluid Mech. 14, 365–393 (1982)
Ranganathan, R., Lewis, R., McCool, C.S., Green, D.W., Willhite, G.P.: Experimental study of the gelation behavior of a polyacrylamide/aluminum citrate colloidal-dispersion gel system. SPE J. December, 337–342 (1998)
Rocha, C.A., Green, D.W., Willhite, G.P., Michnick, M.J.: An experimental study of the interactions of aluminum citrate solutions and silica sand. SPE 18503. In: SPE International Symposium on Oilfield Chemistry. Houston, TX, February 8–10 (1989)
Ryazanov A.V., van Dijke M.I.J., Sorbie K.S.: Two-phase pore-network modeling: existence of oil layers during water invasion. Transp. Porous Media 80, 79–99 (2009)
Porter M.L., Schaap M.G., Wildenschild D.: Simulations of the capillary pressure–saturation–interfacial area relationship for porous media. Adv. Water Resour. 32(11), 1632–1640 (2009)
Sahimi M.: And Transport in Porous Media and Fractured Rock—From Classical Methods to Modern Approaches. Weinheim, VCH (1995)
Salter, S.J., Mohanty, K.K.: Multiphase flow in porous media: 1. Macroscopic observations and modeling. SPE 11017, Society of Petroleum Engineers. The paper was presented at the 57th Annual Fall Technical Conference and Exhibition of the Society of Petroleum Engineers, New Orleans, LA, Sept. 26–29.(1982)
Savins J.: Non-Newtonian flow through porous media. Ind. Eng. Chem. 61(10), 18–47 (1969)
Shah, C.: Flow and immiscible displacement of power-law fluids and bingham plastics in porous media. PhD Thesis, University of Southern California, USA (1994)
Shiyi, Y., Dong, H., Qiang, W., Hua, Y.: Numerical simulator for the combination process of profile control and polymer flooding. SPE 64792. In: SPE International Oil and Gas Conference and Exhibition in China. Beijing, China, 7–10 November (2000)
Singh M., Mohanty K.K: Review: dynamic modeling of drainage through three-dimensional porous materials. Chem. Eng. Sci. 8, 1–18 (2003)
Skauge, A., Ottesen, B.: A summary of experimentally derived relative permeability and residual saturation on north sea reservoir cores. In: International Symposium of the SCA. Monterey, CA, September (2002)
Sorbie K.S.: Polymer-Improved Oil Recovery. Blackie and Son, Bishopbriggs, Glasgow (1991)
Spildo, K., Skauge, A., Aarra, M.G., Tweheyo, M.T.: A new polymer application for north sea reservoirs. SPE 113460. In: SPE/DOE Improved Oil Recovery Symposium. Tulsa, Oklahoma, USA, 20–23 April 2008 (2008)
Szabo M.T.: An evaluation of water-soluble polymers for secondary oil recovery—part 1 and 2. J. Pet. Technol. 31(5), 553–570 (1979)
Van der Marck S.C., Matsuura T., Glas J.: Viscous and capillary pressures during drainage: network simulations and experiments. Phys. Rev. E 56, 5675–5687 (1997)
Valvatne, P.H., Blunt, M.J.: Predictive pore-scale modelling of two-phase flow in mixed wet media. Water Resour. Res. 40, W07406 (2004)
Valvatne P., Piri M., Lopez X., Blunt M.J.: Predictive pore-scale modeling of single and multiphase flow. Transp. Porous Media 55, 71–89 (2004)
Van Brakel J.: Pore space models for transport phenomena in porous media: review and evaluation with special emphasis on capillary liquid transport. Powder Technol. 11, 205–236 (1975)
Van Kats F.M., Egberts P.J.P.: Simulation of three-phase displacement mechanisms using a 2D Lattice–Boltzmann model. Transp. Porous Media 37(1), 55–68 (1999)
Wilkinson D., Willemsen J.F.: Invasion percolation: a new form of percolation theory. J. Phys. A 16, 3365–3376 (1983)
Acknowledgment
The authors would like to acknowledge the PETROMAKS program at the Norwegian Research Council and Statoil for financial support to our EOR research.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Bolandtaba, S.F., Skauge, A. Network Modeling of EOR Processes: A Combined Invasion Percolation and Dynamic Model for Mobilization of Trapped Oil. Transp Porous Med 89, 357–382 (2011). https://doi.org/10.1007/s11242-011-9775-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-011-9775-0