Abstract
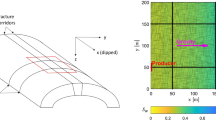
Flow modeling in fractured reservoirs is largely confined to the so-called sugar cube model. Here, however, we consider vertically fractured reservoirs, i.e., the situation that the reservoir geometry can be approximated by fractures enclosed columns running from the base rock to the cap rock (aggregated columns). This article deals with the application of the homogenization method to derive an upscaled equation for fractured reservoirs with aggregated columns. It turns out that vertical flow in the columns plays an important role, whereas it can be usually disregarded in the sugar cube model. The vertical flow is caused by coupling of the matrix and fracture pressure along the vertical faces of the columns. We formulate a fully implicit three-dimensional upscaled numerical model. Furthermore, we develop a computationally efficient numerical approach. As found previously for the sugar cube model, the Peclet number, i.e., the ratio between the capillary diffusion time in the matrix and the residence time of the fluids in the fracture, plays an important role. The gravity number plays a secondary role. For low Peclet numbers, the results are sensitive to gravity, but relatively insensitive to the water injection rate, lateral matrix column size, and reservoir geometry, i.e., sugar cube versus aggregated column. At a low Peclet number and sufficiently low gravity number, the effective permeability model gives good results, which agree with the solution of the aggregated column model. However, ECLIPSE simulations (Barenblatt or Warren and Root (BWR) approach) show deviations at low Peclet numbers, but show good agreement at intermediate Peclet numbers. At high Peclet numbers, the results are relatively insensitive to gravity, but sensitive to the other conditions mentioned above. The ECLIPSE simulations and the effective permeability model show large deviations from the aggregated column model at high Peclet numbers. We conclude that at low Peclet numbers, it is advantageous to increase the water injection rate to improve the net present value. However, at high Peclet numbers, increasing the flow rate may lead to uneconomical water cuts.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Abbreviations
- A :
-
Horizontal cross-section
- B :
-
3D domain
- c :
-
Vector of the matrix-cell center
- d :
-
Size of a grid cell
- D cap :
-
Capillary-Diffusion coefficient
- e :
-
Unit normal vector
- F :
-
Nonlinear fracture function
- F 1,2 :
-
Fracture set
- g :
-
Gravity acceleration
- H :
-
Height of the reservoir
- I :
-
Unit tensor
- k :
-
Permeability
- k f :
-
Effective fracture permeability
- k r :
-
Relative permeability
- l :
-
Local scale (lateral matrix column size)
- L :
-
Global scale/length of the reservoir
- M :
-
Nonlinear matrix function
- n :
-
Unit normal vector
- N f :
-
Number of fracture grid cells
- N G :
-
Gravity number
- N m :
-
Number of matrix grid cells
- N zf :
-
Number of fracture grid cells in the vertical direction
- p :
-
Vector of the fracture-cell center
- P :
-
Pressure
- p c :
-
Capillary pressure
- p′:
-
Vector of the fracture-cell center on a horizontal cross-section
- Pe :
-
Peclet number
- PV:
-
Pore volume
- q :
-
Any parameter
- Q :
-
3D domain
- q ext :
-
External (injection/production) rates
- q w :
-
Water injection rate
- r :
-
Coordinate vector
- R :
-
Real
- S :
-
Saturation
- S or :
-
Residual oil saturation
- S wc :
-
Connate water saturation
- SU:
-
Small unit
- t :
-
Time
- u :
-
Velocity
- u :
-
Velocity vector
- W :
-
Width of the reservoir
- x :
-
x-coordinate
- x b :
-
Global coordinate
- x p :
-
Center of a grid cell
- x s :
-
Local coordinate
- x′:
-
Horizontal cross-section position
- y :
-
y-coordinate
- z :
-
Vertical upward direction
- Z :
-
1D domain
- α :
-
Phase (oil/water)
- ε :
-
Scaling ratio
- λ :
-
Mobility
- μ :
-
Viscosity
- ξ :
-
Potential/saturation indicator
- ρ :
-
Density
- σ :
-
Coordinates of the boundary
- φ :
-
Porosity
- Φ:
-
Potential
- Ω:
-
Horizontal cross-section domain
- ω :
-
Auxiliary function
- 〈 〉:
-
Average sign over volume
- ||:
-
Absolute value of volume
- ≈:
-
Almost equal to
- ⊗:
-
Dyadic product
- \({\surd}\) :
-
Square root
- \({\smallint}\) :
-
Integral
- →:
-
Vector sign
- d:
-
Differential
- ∂ π :
-
Partial differential with respect to π
- ∂:
-
Boundary of
- ∇:
-
Del (gradient operator)
- Δ:
-
Delta (difference operator)
- ∇:
-
Divergence operator
- b:
-
Global (big) index
- D:
-
Dimensionless
- f:
-
Fracture
- m:
-
Matrix
- o:
-
Oil phase
- r:
-
Relative
- R:
-
Reference
- s:
-
Local (small) index
- w:
-
Water phase
- z :
-
z-coordinate (vertical direction)
- α :
-
Oil/water index
- ζ :
-
Fracture/matrix index
- * :
-
Local fracture index
- (0):
-
Zeroth-order index
- (1):
-
First-order index
- (2):
-
Second-order index
References
Aguilera R.: Geological aspects of naturally fractured reservoirs. Lead. Age 17(12), 1667–1670 (1998)
AI-Harbi M., Cheng H., He Z., Datta-Gupta A.: Streamline-based production data integration in naturally fractured reservoirs. Soc. Petrol. Eng. J. 10(4), 426–439 (2005)
Al-Huthali A., Datta-Gupta A.: Streamline simulation of counter-current imbibition in naturally fractured reservoirs. J. Petrol. Sci. Eng. 43(3–4), 271–300 (2004)
Arbogast T.: Gravitational forces in dual-porosity systems: I. Model derivation by homogenization. Transp. Porous Media 13(2), 179–203 (1993a)
Arbogast T.: Gravitational Forces in Dual-Porosity Systems: II. Computational Validation of the Homogenized Model. Transp. Porous Media 13(2), 205–220 (1993b)
Arbogast T.: Computational aspects of dual-porosity models. In: Hornung, U.(eds) Homogenization and Porous Media, Interdisciplinary Applied Mathematics, 6th edn, pp. 203–223. Springer, New York (1997)
Arbogast T., Douglas J. Jr, Hornung U.: Derivation of the double porosity model of single phase flow via homogenization theory. SIAM J. Math. Anal. 21(4), 823–836 (1990)
Barenblatt G.I., Zheltov I.P., Kochina I.N.: Basic concepts in the theory of seepage of homogenous liquids in fissured rocks. J. Appl. Math. Mech. 24(5), 852–864 (1960)
Berkowitz B., Kosakowski G., Margolin G., Scher H.: Application of continuous time random walk theory to tracer test measurements in fractured and heterogeneous porous media. Ground Water 39(4), 593–604 (2001)
Chen Z.: Homogenization and simulation for compositional flow in naturally fractured reservoirs. J. Math. Anal. Appl. 326(1), 12–32 (2007)
De Dreuzy J.-R., Davy P., Bour O.: Hydraulic properties of two-dimensional random fracture networks following power law distributions of length and aperture. Water Resour. Res. 38(12), 121–129 (2002)
De Dreuzy J.-R., Darcel C., Davy P., Bour O.: Influence of spatial correlation of fracture centers on the permeability of two-dimensional fracture networks following a power law length distribution. Water Resour. Res. 40(1), W015021–W0150211 (2004)
Di Donato G., Blunt M.: Streamline-based dual-porosity simulation of reactive transport and flow in fractured reservoirs. Water Resour. Res. 40(4), W042031–W0420312 (2004)
Douglas J. Jr, Hensley J.L., Arbogast T.: A dual-porosity model for waterflooding in naturally fractured reservoirs. Comput. Methods Appl. Mech. Eng. 87(2–3), 157–174 (1991)
Douglas J. Jr, Arbogast T., Paes-Leme P.J., Hensley J.L., Hunes N.P.: Immiscible displacement in vertical fractured reservoirs. Transp. Porous Media 12(1), 73–106 (1993)
Firoozabadi A.: Recovery mechanisms in fractured reservoirs and field performance. J. Can. Petrol. Technol. 39(11), 13–17 (2000)
Hornung U.: Homogenization and Porous Media, Interdisciplinary Applied Mathematics, 6th edn. Springer, New York (1997)
Hoteit H., Firoozabadi A.: Compositional modeling of discrete-fractured media without transfer functions by the discontinuous galerkin and mixed methods. Soc. Petrol. Eng. J. 11(3), 341–352 (2006)
Kazemi H., Seth M.S., Thomas G.W.: The interpretation of interference tests in naturally fractured reservoirs with uniform fracture distribution. Soc. Petrol. Eng. J. 9(4), 463–472 (1969)
Kazemi H., Gilman J.R., Elasharkawy A.M.: Analytical and numerical solution of oil recovery from fractured reservoirs with empirical transfer functions. Soc. Petrol. Eng. Reserv. Eng. 7(2), 219–227 (1992)
Lewandowska J., Szymkiewicz A., Auriault J.L.: Upscaling of Richards’ equation for soils containing highly conductive inclusions. Adv. Water Resour. 28, 1159–1170 (2005)
Margolin G., Berkowitz B., Scher H.: Structure, flow, and generalized conductivity scaling in fracture networks. Water Resour. Res. 34(9), 2103–2121 (1998)
Nelson R.A.: Geologic Analysis of Naturally Fractured Reservoirs. Gulf Publishing Co., Houston, TX (1985)
Park Y.-J., de Dreuzy J.-R., Lee K.-K., Berkowitz B.: Transport and intersection mixing in random fracture networks with power law length distributions. Water Resour. Res. 37(10), 2493–2501 (2001)
Pooladi-Darvish M., Firoozabadi A.: Cocurrent and countercurrent imbibition in a water-wet matrix block. Soc. Petrol. Eng. J. 5(1), 3–11 (2000)
Salimi, H., Bruining, J.: Improved prediction of oil recovery from waterflooded fractured reservoirs using homogenization. Soc. Petrol. Eng. Reserv. Eng. Eval. (2009). doi:10.2118/115361-PA
Sarma P., Aziz K.: New transfer function for simulation of naturally fractured reservoirs with dual-porosity models. Soc. Petrol. Eng. J. 11(3), 328–340 (2006)
Shook M., Li D., Lake L.W.: Scaling immiscible flow through permeable media by inspectional analysis. In Situ 16(4), 311–349 (1992)
Sonier F., Souillard P., Blaskovich F.T.: Numerical simulation of naturally fractured reservoirs. Soc. Petrol. Eng. Reserv. Eng. 3(4), 1114–1122 (1988)
Tartar L. : Incompressible fluid flow in a porous medium—convergence of the homogenization process. In: Sanchez-Palencia, E. (eds) Lecture Notes in Physics, vol. 127, pp. 368–377. Springer, New York (1980)
Van Duijn C.J., Molenaar J., Neef M.J.: The effect of capillary forces on immiscible two-phase flow in heterogeneous porous media. Transp. Porous Media 21(1), 71–93 (1995)
Van Duijn C.J., Mikelić A., Pop I.S.: Effective equations for two-phase flow with trapping on the micro scale. SIAM J. Appl. Math. 62(5), 1531–1562 (2002)
Van Duijn C.J., Mikelić A., Pop I.S., Rosier C.: Effective dispersion equations for reactive flows with dominant Péclet and Damkohler numbers. Adv. Chem. Eng. 34, 1–45 (2008)
Warren J.E., Root P.J.: The behavior of naturally fractured reservoirs. Soc. Petrol. Eng. J. 3(3), 245–255 (1963)
Wu Y.S., Pan L., Pruess K.: A physically based approach for modeling multiphase fracture–matrix interaction in fractured porous media. Adv. Water Resour. 27, 875–887 (2004)
Yortsos, Y.C.: A theoretical analysis of vertical flow equilibrium. Paper SPE 22612 presented at the SPE annual technical conference and exhibition, Dallas, TX, 6–9 October 1991. doi:10.2118/22612-MS
Acknowledgments
We thank Statoil-Hydro for supporting our research on oil recovery from fractured reservoirs. We also thank Sharif University of Technology for their steady collaboration. We acknowledge Maryam Namdar Zanganeh, William R. Rossen, Stefan M. Luthi, and Giovanni Bertotti for many useful discussions and comments. We also acknowledge SPE for granting the Nico van Wingen Memorial Graduate Fellowship in Petroleum Engineering to Hamidreza Salimi.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Salimi, H., Bruining, H. Upscaling in Vertically Fractured Oil Reservoirs Using Homogenization. Transp Porous Med 84, 21–53 (2010). https://doi.org/10.1007/s11242-009-9483-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-009-9483-1