1 Introduction

There is increasingly important trend in domains such as automotive systems, avionics, and medical engineering towards integrating functions with different levels of criticality onto a common hardware platform. This allows for a reduction of costs and complexity, however, it leads to mixed-criticality (MC) systems that require careful design and analysis. In particular, it must be guaranteed that high-criticality (HI) functions/tasks are not affected by low-criticality (LO) tasks that share the same resources.

In this paper, we are concerned with scheduling a mix of HI and LO tasks under EDF and on one processor—however, a discussion for more levels of criticality is presented in the appendix. In particular, we make use of Vestal’s task model (Vestal 2007). That is, LO tasks are modeled by only one worst-case execution time (WCET) (apart from inter-arrival time and deadline), while HI tasks are characterized by an optimistic and by a conservative WCET to account for potential increases in execution demand (Vestal 2007). In this context, a standard real-time scheduling requires guaranteeing that LO and HI tasks meet their deadlines when HI tasks’ conservative WCETs are considered. However, since HI tasks run for at most their optimistic WCETs almost all the time, this leads to an inefficient design. On the other hand, if only optimistic WCETs are considered, HI tasks may occasionally miss their deadlines.

To overcome this predicament, a common approach is to implement two operation modes.Footnote 1 In LO mode, HI tasks run for their optimistic WCETs and are scheduled within virtual deadlines together with all LO tasks. Virtual deadlines are given by \(x_i\cdot D_i\) and are usually shorter than real deadlines \(D_i\) with \(x_i\in (0,1]\) being referred to as deadline scaling factor. The system switches to HI mode, when one or more HI tasks require running for longer (up to their conservative WCETs). HI tasks are then scheduled within their real deadlines and LO tasks are stopped from running (i.e., discarded).

In such a setting, apart from guaranteeing schedulability of individual modes, it is necessary to guarantee schedulability of transitions between modes. However, since transitions between LO and HI mode can happen at arbitrary points in time, carry-over jobs cannot be avoided, i.e., HI jobs that are released prior to, but have not finished executing at the moment of the transition.

Approaches from the literature such as GREEDY (Ekberg and Yi 2012) and ECDF (Easwaran 2013) focus on bounding execution demand by carry-over jobs, resulting in relatively complex algorithms. In this paper, we propose a novel technique that works around the computation of carry-over execution demand. We prove that transitions between LO and HI mode are feasible, if an equivalent task set derived from the original one is schedulable under plain EDF. This not only reduces the overall complexity, but it also improves our understanding on MC scheduling. Moreover, we can apply well-known approximation techniques such as Devi’s test (Devi 2003) to trade off accuracy for complexity/runtime. We present a large set of experiments based on synthetic data illustrating the benefits of the proposed approach in term of weighted schedulability and runtime compared to the most prominent approaches from the literature.

The rest of the paper is structured as follows. Related work is briefly discussed in Sect. 2. Section 3 introduces the task model and assumptions used, whereas Sect. 4 deals with the proposed technique for bounding execution demand under mixed-criticality EDF and perform an analytical comparison with the GREEDY and the ECDF algorithm in Sect. 5. Further, we apply Devi’s test in Sect. 6 to derive two approximated variants of our proposed approach, i.e., based on per-task and on uniform deadline scaling. In Sect. 7, we present extensive experimental results evaluating the proposed technique, whereas Sect. 8 concludes the paper. Finally, in the appendix, we briefly investigate how to extend the proposed technique to more than two levels of criticality.

2 Related work

In this section, we briefly revise the rich literature concerning scheduling MC tasks on one processor and, in particular, under EDF—a complete overview can be found in Burns and Davis (2018).

The problem around MC systems was first addressed by Vestal in (2007), who proposed modeling HI tasks with multiple WCET parameters to account for potential increases in execution demand. Based on this model, Baruah et al. later analyzed per-task priority assignments and the resulting worst-case response times (Baruah et al. 2011b).

In Baruah et al. (2011a), Baruah et al. also proposed the EDF-VD algorithm to schedule a mix of HI and LO tasks. EDF-VD introduces two operation modes and uses a priority-promotion scheme by uniformly scaling deadlines of HI tasks. The resulting speed-up factor was shown to be equal to \((\sqrt{5}+1)/2\) (Baruah et al. 2011a). Later this speed-up factor was improved to 4/3 (Baruah et al. 2012). Baruah et al. further proposed extensions to EDF-VD, where, in particular, a per-task deadline scaling is used (Baruah et al. 2015). However, they also concluded that the speed-up factor of 4/3 cannot be improved (Baruah et al. 2015). Similarly, Müller presented a more general per-task deadline scaling technique that allows improving schedulability (Müller 2016).

Improvements to the original EDF-VD have also been proposed by other authors. In Su and Zhu (2013), Su and Zhu used an elastic task model Kuo and Mok (1991) to improve resource utilization in MC systems. In Zhao et al. (2013), Zhao et al. applied preemption thresholds Wang and Saksena (1999) in MC scheduling in order to better utilize the processing unit. In Masrur et al. (2015), a technique consisting of two scaling factors is proposed for admission control in MC systems.

A more flexible approach referred to as GREEDY with per-task deadline scaling was presented by Ekberg and Yi for the case of two criticality levels (Ekberg and Yi 2012). Ekberg and Yi characterized the execution demand of MC systems under EDF by deriving demand bound functions for the LO and the HI mode. Later, they extended this work to the case of more than two criticality levels (Ekberg and Yi 2014). In Easwaran (2013), Easwaran presented a similar technique called ECDF also for the case of two criticality levels and showed that it strictly dominates the GREEDY approach.

In contrast to GREEDY and ECDF, in Mahdiani and Masrur (2018), we proposed working around the computation of carry-over execution demand at transitions between LO and HI mode. In particular, testing schedulability of transitions from LO to HI reduces to testing schedulability of an equivalent task set under plain EDF (Mahdiani and Masrur 2018). In this paper, we extend this work and propose using approximation techniques, particularly, Devi’s test to derive schedulability tests for MC systems under EDF that trade off accuracy versus performance as discussed later in detail.

3 Models and assumptions

In this section, we discuss most of our notation. Similar to Ekberg and Yi (2012) and Easwaran (2013), we basically adopt the task model originally proposed in Vestal (2007). We consider a set \(\tau\) of MC tasks that are independent, preemptable and sporadic running on one processor under preemptive EDF scheduling. Each individual task \(\tau _i\) in \(\tau\) is characterized by its minimum inter-release time \(T_i\), i.e., the minimum distance between two consecutive jobs or instances of a task, and by its relative deadline \(D_i\) with \(D_i \le T_i\forall i\). Further, we assume that tasks do not self-suspend and that the overhead by context switches has been accounted for in tasks’ WCETs or can be neglected.

As already stated, we are concerned with dual-criticality systems with two levels of criticality, namely LO and HI.Footnote 2 The criticality of a task \(\tau _i\) is denoted by \(\chi _i\) with:

$$\begin{aligned} \chi _i \in \{LO,HI\}. \end{aligned}$$

A LO task is associated with only one WCET value/estimate denoted by \(C_i^{LO}\). Opposed to this, a HI task is characterized by its optimistic WCET estimate \(C_i^{LO}\) and its conservative WCET estimate \(C_i^{HI}\) with:Footnote 3

$$\begin{aligned} C_i^{LO}< C_i^{HI}\le D_i\le T_i. \end{aligned}$$

The system basically distinguishes two operation modes denoted by m: LO and HI mode. In LO mode, HI tasks execute for no longer than \(C_i^{LO}\), whereas these might require executing for up to \(C_i^{HI}\) in HI mode. The system initializes in LO mode where all LO and HI tasks need to meet their deadlines. As soon as one job of a HI task executes for longer than its \(C_i^{LO}\), the system switches to HI mode discarding all LO tasks. Similar to context switches, we assume that the overhead by mode switches has been accounted for in \(C_i^{HI}\).

Finally, we denote the utilization by LO and HI tasks in the LO and HI mode respectively as follows:

$$\begin{aligned} U_{\chi }^{m}:=\sum \limits _{\chi _i=\chi } \frac{C_i^m}{T_i}, \end{aligned}$$

where again \(\chi\) and m can assume values in \(\{LO,HI\}\). Note that only \(U_{LO}^{LO}\), \(U_{HI}^{LO}\) and \(U_{HI}^{HI}\) exist. \(U_{LO}^{HI}\) is effectively zero, since LO tasks are dropped and, hence, do not run in HI mode.

3.1 Mixed-criticality EDF

A common approach when scheduling MC systems is to shorten the deadlines of HI jobs in LO mode. This way, processor capacity can be reserved for a potential switch to HI mode—where HI tasks require more execution demand. In other words, we assign a virtual deadline equal to \(x_i\cdot D_i\) with \(x_i \in (0,1]\) to all \(\tau _i\) with \(\chi _i=HI\).

This virtual deadline is used instead of \(D_i\)—the real deadline—to schedule HI tasks in LO mode. The parameter \(x_i\) is the so-called deadline scaling factor. There is no deadline scaling for LO tasks such that they are scheduled (only in LO mode) using their \(D_i\).

When the system switches to HI mode, HI tasks start being scheduled according to their real deadlines \(D_i\) whereas LO tasks are discarded immediately. In this paper, we consider that tasks are scheduled under EDF in both modes and refer to this scheme as mixed-criticality EDF.

Clearly, whereas schedulability of separated modes can be easily tested, i.e., when the system is stable in either LO or HI mode, it is difficult to test schedulability of transitions between modes. In particular, careful analysis is required when the system switches from LO to HI mode.

In this paper, similar to other approaches from the literature, transitions from HI back to LO mode are disregarded. The reason is that, in contrast to changes from LO to HI, a change from HI to LO mode can be programmed or postponed to a suitable point in time, e.g., at which the processor idles, and does not require further analysis.

3.2 The EDF-VD algorithm

EDF with Virtual Deadlines (EDF-VD) is a special case of mixed-criticality EDF for the case \(D_i=T_i\) \(\forall i\). Under EDF-VD, virtual deadlines are obtained by \(x\cdot D_i\), where \(x\in (0,1]\) is a uniform deadline scaling factor for all HI tasks (Baruah et al. 2011a).

Under EDF-VD, the LO and HI tasks need to be schedulable with their corresponding \(C^{LO}_i\) under EDF in LO mode. Similarly, in HI mode, the HI tasks also need to be schedulable with their corresponding \(C^{HI}_i\) under EDF. As a result, the following two schedulability conditions are necessary:

$$\begin{aligned} U_{LO}^{LO}+U_{HI}^{LO}\le & {} 1 \end{aligned}$$
(1)
$$\begin{aligned} U_{HI}^{HI}\le & {} 1 \end{aligned}$$
(2)

Note that these two conditions do not ensure schedulability in the transition phase. Hence, they are indeed only necessary, but not sufficient conditions. In Baruah et al. (2012), Baruah et al. also obtained a sufficient schedulability condition for EDF-VD in the form of a utilization bound: \(\max \bigl (U_{LO}^{LO} + U_{HI}^{LO},U_{HI}^{HI}\bigr ) \le 3/4\). They also proposed a more accurate schedulability test based on whether feasible lower and upper bounds can be obtained on x (Baruah et al. 2012):

$$\begin{aligned} \frac{U_{HI}^{LO}}{1-U_{LO}^{LO}}\le & {} x, \end{aligned}$$
(3)
$$\begin{aligned} x\le & {} \frac{1 - U_{HI}^{HI}}{U_{LO}^{LO}}. \end{aligned}$$
(4)

That is, if the value of x obtained with (3) is less than or equal to the value obtained with (4), then it is possible to find a valid x for the considered system rendering it schedulable under EDF-VD.

4 Bounding execution demand

In this section, we are concerned with characterizing execution demand by \(\tau\) under mixed-criticality EDF. In Ekberg and Yi (2012) and Easwaran (2013), a demand bound function was presented for each mode in the system, i.e., one for the LO mode and one for the HI mode. As mentioned above, we derive a third demand bound function for the transition between modes. This allows working around the computation of carry-over execution demand, reducing the amount of pessimism and, hence, relaxing schedulability conditions in HI mode (Mahdiani and Masrur 2018).

4.1 Schedulability in LO mode

In LO mode, LO tasks need to scheduled together with HI tasks, while the latter are assigned virtual deadlines \(x_i\cdot D_i\). As a consequence, the resulting demand bound function \(\text {dbf}_{LO}(t)\) in LO mode is given by:

$$\begin{aligned} \text {dbf}_{LO}(t)= & {} \sum \limits _{\chi _i=LO}\left( \left\lfloor \frac{t-D_i}{T_i}\right\rfloor +1\right) C_{i}^{LO}\nonumber \\&+\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{t-x_i\cdot D_i}{T_i}\right\rfloor +1\right) C_{i}^{LO}. \end{aligned}$$
(5)

Here \(t\ge 0\) is a (real) number representing time, i.e., \(\text {dbf}_{LO}(t)\) returns a \(\tau\)’s maximum execution demand in LO mode in an interval of length t. Note that \(\text {dbf}_{LO}(t)\) is always greater than or equal to zero, since \(D_i\le T_i\) holds for all \(\tau _i\) and \(x_i\) has values in (0, 1].

The system is schedulable in LO mode, if \(\text {dbf}_{LO}(t)\le t\) holds for all possible t until the processor first idles (Baruah et al. 1990). That is, until a point in time \(\hat{t}_{LO}\) for which the following holds:

$$\begin{aligned} \hat{t}_{LO}= & {} \sum \limits _{\chi _i=LO}\left( \left\lfloor \frac{\hat{t}_{LO}-D_i}{T_i}\right\rfloor +1\right) C_{i}^{LO}\\&+\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{\hat{t}_{LO}-x_i\cdot D_i}{T_i}\right\rfloor +1\right) C_{i}^{LO}, \end{aligned}$$

where removing the floor function leads to:

$$\begin{aligned} \hat{t}_{LO}\le & {} \sum \limits _{\chi _i=LO}\left( \frac{\hat{t}_{LO}-D_i}{T_i}+1\right) C_{i}^{LO} \\&+\sum \limits _{\chi _i=HI}\left( \frac{\hat{t}_{LO}-x_i\cdot D_i}{T_i}+1\right) C_{i}^{LO}, \end{aligned}$$

and reshaping to:

$$\begin{aligned} \hat{t}_{LO}\le & {} \hat{t}_{LO}\left( \sum \limits _{\chi _i=LO}\frac{C_{i}^{LO}}{T_i}+\sum \limits _{\chi _i=HI}\frac{C_{i}^{LO}}{T_i}\right) \\&+\sum \limits _{\chi _i=LO}(T_i-D_i)\frac{C_{i}^{LO}}{T_i}+\sum \limits _{\chi _i=HI}(T_i-x_i\cdot D_i)\frac{C_{i}^{LO}}{T_i}. \end{aligned}$$

Finally, considering that \(U_{LO}^{LO}=\sum _{\chi _i=LO}\frac{C_{i}^{LO}}{T_i}\) and \(U_{HI}^{LO}=\sum _{\chi _i=HI}\frac{C_{i}^{LO}}{T_i}\), we obtain an upper bound on \(\hat{t}_{LO}\):

$$\begin{aligned} \hat{t}_{LO}\le & {} \frac{\sum \limits _{\chi _i=LO}(T_i-D_i)\frac{C_{i}^{LO}}{T_i}}{1-U_{LO}^{LO}-U_{HI}^{LO}}+\frac{\sum \limits _{\chi _i=HI}(T_i-x_i\cdot D_i)\frac{C_{i}^{LO}}{T_i}}{1-U_{LO}^{LO}-U_{HI}^{LO}}. \end{aligned}$$
(6)

The bound in (6) depends on the values of \(x_i\), which are not known a priori. On the other hand, note that this bound maximizes when all \(x_i\) tend to 0, which then leads to the following:

$$\begin{aligned} \hat{t}_{LO}\le & {} \frac{\sum \limits _{\chi _i=LO}(T_i-D_i)\frac{C_{i}^{LO}}{T_i}}{1-U_{LO}^{LO}-U_{HI}^{LO}}+\frac{\sum \limits _{\chi _i=HI}C_{i}^{LO}}{1-U_{LO}^{LO}-U_{HI}^{LO}}, \end{aligned}$$
(7)

Clearly, \(U_{LO}^{LO}+U_{HI}^{LO}\)—the utilization in LO mode—must be strictly less than one in order that (6) and (7) return valid and finite values.

4.2 Schedulability in stable HI mode

In this case LO tasks do not run and HI tasks run for their corresponding \(C_{i}^{HI}\) leading to the following demand bound function:

$$\begin{aligned} \text {dbf}_{HI}(t)=\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{t-D_i}{T_i}\right\rfloor +1\right) C_{i}^{HI}, \end{aligned}$$
(8)

where again \(t\ge 0\) is a (real) number representing time, i.e., \(\text {dbf}_{HI}(t)\) returns the maximum execution demand in a time interval of length t.

The system is schedulable in stable HI mode, if \(\text {dbf}_{HI}(t)\le t\) for all possible t until the processor first idles, i.e., until a point in time \(\hat{t}_{HI}\) is reached where \(\text {dbf}_{HI}(\hat{t}_{HI})=\hat{t}_{HI}\). We again can remove the floor function in (8) to obtain an upper bound on \(\hat{t}_{HI}\):

$$\begin{aligned} \hat{t}_{HI}\le \frac{\sum \limits _{\chi _i=HI}(T_i-D_i)\frac{C_{i}^{HI}}{T_i}}{1-U_{HI}^{HI}}. \end{aligned}$$
(9)

\(U_{HI}^{HI}\)—the utilization in HI mode—must be strictly less than one in order that (9) returns a valid and finite upper bound on \(\hat{t}_{HI}\).

4.3 Schedulability in the transition from LO to HI mode

The transition from LO to HI mode may happen at an arbitrary point in time when one HI job exceeds its LO execution budget \(C_{i}^{LO}\). Unfinished LO jobs are discarded at that time; however, the problem arises with HI jobs that were released before but have not finished executing their \(C_{i}^{LO}\), i.e., carry-over jobs. Since it is difficult to accurately bound the execution demand by carry-over jobs, usually, pessimistic assumptions need to taken.

The following theorem, is a generalization of a theorem in Masrur et al. (2015) and allows working around carry-over jobs and characterizing the additional execution demand in the transitions from LO to HI mode in a more effective manner. In other words, this theorem allows us to guarantee schedulability without computing carry-over execution demand at the point of switching from LO to HI mode.

Theorem 1

Given a set \(\tau\) of MC tasks, let us assume that(i) \(\text {dbf}_{LO}(t)\le t\) and (ii) \(\text {dbf}_{HI}(t)\le t\) hold for \(0< t\le \hat{t}_{LO}\) and \(0< t\le \hat{t}_{HI}\) respectively, i.e., \(\tau\) is schedulable in LO and stable HI mode. The transition from LO to HI mode is schedulable under mixed-criticality EDF, if \(\text {dbf}_{SW}(t)\le t\) also holds for \(0<t\le \hat{t}_{SW}\), where \(\text {dbf}_{SW}(t)\) is given by:

$$\begin{aligned} \text {dbf}_{SW}(t)=\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{t-\Delta D_i}{T_i}\right\rfloor +1\right) \Delta C_{i}, \end{aligned}$$
(10)

with \(\Delta D_i=D_i-x_i\cdot D_i\), \(\Delta C_i=C_i^{HI}-C_i^{LO}\), and \(\hat{t}_{SW}\) is upper bounded by the following expression:

$$\begin{aligned} \hat{t}_{SW}\le \frac{\sum \limits _{\chi _i=HI}\Delta C_{i}}{1-U_{HI}^{SW}}, \end{aligned}$$
(11)

where \(U_{HI}^{SW}\) is given by \(\sum \limits _{\chi _i=HI}\frac{\Delta C_i}{T_i}\).

Proof

Let us consider that the system switches to HI mode at time \(t'\) and that the processor idles for the first time thereafter at \(t''\) with \(t'< t''\), i.e., all jobs released prior to \(t''\) finish executing at latest by \(t''\). Clearly, jobs that are released after \(t''\) are guaranteed schedulable by assumption (ii).

Let us now assume that a deadline is missed for the first time at \(t_{miss}\) by a job of any \(\tau _i\) that we denote \(\tau _{miss}\). Clearly, \(t_{miss}\) must be in the interval \([t',t'']\) and the following must hold for \(\delta _{miss}=t_{miss}-t'\):

$$\begin{aligned} \delta _{miss}<CO+\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{\delta _{miss}-\phi _i-D_i}{T_i}\right\rfloor +1\right) C_{i}^{HI}, \end{aligned}$$

where \(\phi _i=r'_i-t'\) is the phase of a \(\tau _i\) at \(t'\), i.e., the release time \(r'_i\) of its first job after \(t'\) minus \(t'\). Note that \(\phi _i\) is in the interval \([0,T_i)\). In addition, CO denotes the carry-over execution demand at \(t'\). This is the amount of execution in \([t',t_{miss}]\) by HI jobs that are released prior to \(t'\), but have not finished executing at \(t'\).

As already discussed, it is difficult to determine CO in an accurate manner. Hence, to work around CO, let us first divide each \(\tau _i\), whose jobs have both release times and deadlines in \([t',t_{miss}]\), into two subtasks. The first subtask—denoted by \(\tau _i^{LO}\)—is released for the first time at \(\phi _i\) and requires executing \(C_i^{LO}\) within \(x_i\cdot D_i\) every \(T_i\) time, i.e., this represents \(\tau _i\)’s execution demand in LO mode. The second subtask—denoted by \(\tau _i^{SW}\)—is released for the first time at \(\phi '_i=\phi _i+x_i\cdot D_i\) and requires executing \(\Delta C_i=C_i^{HI}-C_i^{LO}\) within \(\Delta D_i=D_i-x_i\cdot D_i\) every \(T_i\) time, i.e., this presents \(\tau _i\)’s increase in execution demand incurred in HI mode. Note that, in spite of this modification, the total amount of execution demand in \([t',t_{miss}]\) does not change, i.e., a deadline is still missed at \(t_{miss}\) as per assumption, and we can reshape the above inequality to:

$$\begin{aligned} \delta _{miss}< & {} CO+\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{\delta _{miss}-\phi _i-x_i\cdot D_i}{T_i}\right\rfloor +1\right) C_{i}^{LO}\nonumber \\&\!\!\!\!+\sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{\delta _{miss}-\phi '_i-\Delta D_i}{T_i}\right\rfloor +1\right) \Delta C_{i}. \end{aligned}$$
(12)

Note that \(t_{miss}\) coincides with the deadline of the corresponding job of \(\tau _{miss}^{SW}\), which misses its deadline. (Recall that \(\tau _{miss}\) is now divided into the subtasks \(\tau ^{LO}_{miss}\) and \(\tau ^{SW}_{miss}\).) Now, there are two possible cases to consider in order to prove this theorem: The set of only subtasks \(\tau _i^{SW}\) is either (1) unschedulable or (2) schedulable in isolation.

Case (1): This is a rather trivial case. If the set of only \(\tau _i^{SW}\) is unschedulable in isolation, i.e., when scheduled alone on a single processor, \(\text {dbf}_{SW}(t)>t\) must hold for some t in \([0,\hat{t}_{SW}]\) with \(\text {dbf}_{SW}(t)\) given as per (10). As a result, we will be able to detect a deadline miss in the transition between LO and HI mode by only testing the set of all \(\tau _i^{SW}\).

To this end, we need to find an upper bound on \(\hat{t}_{SW}\) making \(\text {dbf}_{SW}(\hat{t}_{SW})=\hat{t}_{SW}\) and removing the floor function as before:

$$\begin{aligned} \hat{t}_{SW} \le \frac{\sum \limits _{\chi _i=HI}(T_i-\Delta D_i)\frac{\Delta C_{i}}{T_i}}{1-U_{HI}^{SW}}. \end{aligned}$$

Here, \(U_{HI}^{SW}=\sum _{\chi _i=HI}\frac{\Delta C_i}{T_i}\) is the utilization of the set of only \(\tau _i^{SW}\). Since \(U_{HI}^{SW}<1\) holds by assumption (ii), the above inequality returns a valid bound on \(\hat{t}_{SW}\). This depends on \(\Delta D_i=D_i-x_i\cdot D_i\) and, therefore, on the values of \(x_i\), which we do not know in advance. However, we can make \(x_i=1\) for all i leading to the upper bound in (11).

Case (2): We show that this case leads to a contradiction. To this end, recall that we assumed that a deadline is missed for the first time at \(t_{miss}\), hence, all previous jobs in \([t',t_{miss})\) can actually finish executing in time. Since now \(\tau _{miss}\) is divided into the subtasks \(\tau ^{LO}_{miss}\) and \(\tau ^{SW}_{miss}\), the \(\tau _{miss}^{LO}\)’s job with a deadline equal to \(t_{miss}-\Delta D_{miss}\) must push carry-over \(\tau _i^{SW}\)’s jobs (i.e., those that are released prior to and have not finished executing at \(t_{miss}-\Delta D_{miss}\) and that have deadlines prior to \(t_{miss}\)) by at least \(\Delta _{miss}\) being \(\Delta _{miss}\) the amount of the deadline miss at \(t_{miss}\). Otherwise, no deadline can be missed at \(t_{miss}\), since \(\text {dbf}_{SW}(t)\le t\) is assumed to hold for all t. In addition, note that the processor does not idle in \([t_{miss}-\Delta D_{miss},t_{miss}]\).

Fig. 1
figure 1

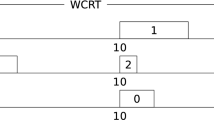
Illustration of Case (2.a) with \(\Delta D_i\le \Delta D_{miss}\): The carry-over \(\tau _i^{SW}\)’s job is illustrated in green and \(\tau _{miss}^{SW}\) is illustrated in red. The light green and red shading represent \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\) respectively, whereas a light gray shading represents any previous higher-priority execution (i.e., of jobs with shorter deadlines). Solid upward arrows stand for the release times of \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\), while dashed upward arrows represent the release times of \(\tau _i^{SW}\) and \(\tau _{miss}^{SW}\) (which are also the (virtual) deadlines of \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\)). Solid downward arrows stand for the (real) deadlines of \(\tau _i^{SW}\) and \(\tau _{miss}^{SW}\) (Color figure online)

Full size image

Case (2.a): Let us assume that there is only one carry-over job of an arbitrary \(\tau _i^{SW}\) and that \(\Delta D_i\le \Delta D_{miss}\) holds. Note that, after moving this job forward to force its release time to coincide at \(t_{miss}-\Delta D_{miss}\), \(\tau _{miss}^{SW}\)’s job continues to miss its deadline by at least \(\Delta _{miss}\) at \(t_{miss}\), since the deadline of this carry-over \(\tau _i^{SW}\)’s job remains within the interval \([t_{miss}-\Delta D_{miss},t_{miss}]\). As a result, the amount of execution demand in \([t_{miss}-\Delta D_{miss}, t_{miss}]\) remains the same or even increases after this displacement—see Fig. 1.

The above analysis leads to a contradiction, since \(\tau _{miss}^{SW}\)’s job and its carry-over \(\tau _i^{SW}\)’s job are now released in synchrony at \(t_{miss}-\Delta D_{miss}\). Consequently, \(\tau _{miss}^{LO}\) cannot push any additional execution demand into \([t_{miss}-\Delta D_{miss},t_{miss}]\) and, hence, if a deadline is missed at \(t_{miss}\), \(\text {dbf}_{SW}(t)\le t\) cannot hold for all t.

Fig. 2
figure 2

Illustration of Case (2.b) with \(\Delta D_i>\Delta D_{miss}\): The carry-over \(\tau _i^{SW}\)’s job is illustrated in green and \(\tau _{miss}^{SW}\) is illustrated in red. The light green and red shading represent \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\) respectively, whereas a light gray shading represents any previous higher-priority execution (i.e., of jobs with shorter deadlines). Solid upward arrows stand for the release times of \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\), while dashed upward arrows represent the release times of \(\tau _i^{SW}\) and \(\tau _{miss}^{SW}\) (which are also the (virtual) deadlines of \(\tau _i^{LO}\) and \(\tau _{miss}^{LO}\)). Solid downward arrows stand for the (real) deadlines of \(\tau _i^{SW}\) and \(\tau _{miss}^{SW}\) (Color figure online)

Full size image

Case (2.b): Let us now assume that there is again only one carry-over job of an arbitrary \(\tau _i^{SW}\), however, \(\Delta D_i> \Delta D_{miss}\) holds this time. Note that we can displace this carry-over \(\tau _i^{SW}\)’s job forward until its deadline occurs at \(t_{miss}+\epsilon\), where \(\epsilon\) is an infinitesimally small number greater than zero. As a result, this \(\tau _i^{SW}\)’s job starts missing its deadline by an amount equal to at least \(\Delta _{miss}-\epsilon\), since at least the original execution demand in \([t_{miss}-\Delta D_{miss},t_{miss}]\) is executed in \([t_{miss}-\Delta D_{miss},t_{miss}+\epsilon ]\)—see Fig. 2.

It is easy to see that we can now apply the analysis of Case (2.a) where the carry-over \(\tau _i^{SW}\)’s job of this case misses its deadline at \(t_{miss}+\epsilon\) (by an amount of at least \(\Delta _{miss}-\epsilon\)) and the \(\tau _{miss}^{SW}\)’s job of this case becomes the carry-over job in Case (2.a). As a result, Case (2.b) also leads to a contradiction, i.e., if a deadline is missed at \(t_{miss}\), \(\text {dbf}_{SW}(t)\le t\) cannot hold for all t.

Clearly, there can be several carry-over jobs whose execution demands are pushed (at least partially) by \(\tau _{miss}^{LO}\) into \([t_{miss}-\Delta D_{miss}, t_{miss}]\), however, the total amount of execution demand pushed by \(\tau _{miss}^{LO}\) remains \(\Delta _{miss}\). In this latter case, again, it is easy to see that we can apply the analysis of Case (2.a) and Case (2.b) to each individual carry-over job. Consequently, if a deadline is missed at \(t_{miss}\), \(\text {dbf}_{SW}(t)> t\) must hold for some t. The theorem follows. \(\square\)

Theorem 1 allows characterizing the additional execution demand in the transitions from LO to HI mode independent of carry-over jobs. Based on it, we test whether deadlines are met or not in \([t',t'']\), i.e., from the time \(t'\) of switching to HI mode to the time \(t''\) at which the processor first idles after switching.

figure a

4.4 Finding deadline scaling factors

Now, we propose an algorithm to find valid values of \(x_i\) for each HI task in \(\tau\). Clearly, this is closely related to the technique used to tighten deadlines in LO mode. In this paper, however, we do not aim to improve deadline tightening. The contribution is rather a new technique for bounding demand execution, which can be combined with existing deadline tightening techniques, e.g., from Ekberg and Yi (2012) or Easwaran (2013).

The proposed algorithm shown in Algorithm 1 essentially tests \(\tau\)’s schedulability in the LO mode (line 1), and in HI mode (line 2). If \(\tau\) is schedulable in LO mode, the function testLO() returns a vector \(\text {X}_{LW}\) with the minimum values of \(x_i\) that could be found to be valid. If this vector is not empty, i.e., valid \(x_i\) values could be found, and \(\tau\) is schedulable in HI mode, Algorithm 1 tests schedulability at the transitions from LO to HI mode (line 3).

Further, if the set of HI tasks in \(\tau\)—denoted by \(\tau _{HI}\)—is schedulable at transitions from LO to HI, the function testSW() returns a vector \(\text {X}_{U\!P}\) with the minimum values of \(1-x_i\) that are also valid. That is, if \(\text {X}_{U\!P}\) is neither empty, the whole \(\tau\) will be schedulable under mixed-criticality EDF provided that \(\text {X}_{LW}\le \mathbf {1}-\text {X}_{U\!P}\) holds (line 4). Here, \(\mathbf {1}\) denotes a unity vector (where all elements are equal to one). That is, for each element in the vectors \(\text {X}_{LW}\) and \(\text {X}_{U\!P}\), the following condition must hold:

$$\begin{aligned}&\text {X}_{LW}(i)\le x_i, \\&\text {X}_{U\!P}(i)\le 1-x_i, \\&\implies x_i \le 1-\text {X}_{U\!P}(i). \end{aligned}$$
figure b

As already mentioned, the functions testLO() and testSW()—shown in Algorithms 2 and  3—test schedulability in LO mode and at the transitions from LO to HI mode. These two functions are very similar—apart from testLO() dealing with the whole \(\tau\) and testSW() with the subset \(\tau _{HI}\)—and return lower bounds on \(x_i\) and on \(1-x_i\) respectively. Thus, the following discussion of testLO() also applies to testSW().

Basically, testLO() computes \(\text {dbf}_{LO}(t)\) for all \(0\le t\le \hat{t}_{LO}\) starting from \(x_i=1\) for all HI tasks. However, at least the first deadline of each task should be checked, since we need to compute each \(x_i\). That is, we need to compute \(\text {dbf}_{LO}(t)\) at least until \(D_{max}=\max \limits _{\forall i}(D_i)\)—see line 3 in Algorithm 2. If the current t corresponds to a deadline of a HI task (lines 10–14), its (relative) virtual deadline \(x_i\cdot D_i\) is adjusted such that its absolute deadline \(r_i+x_i\cdot D_i\) is equal to \(\text {dbf}_{LO}(t)\) (i.e., the total execution demand at t).

Note that the execution demand of jobs with prior deadlines to t is contained in \(\text {dbf}_{LO}(t)\). As a result, the computed \(x_i\) in line 12 can never compromise schedulability of these previous jobs. In addition, an \(x_i\) currently being computed can only replace a previously computed \(x_i\), if either this is the first value of \(x_i\) computed for the corresponding \(\tau _i\), i.e., t coincides with the first deadline of \(\tau _i\), or this is greater than the previous value of \(x_i\) (lines 11 to 13). In other words, after initialization, the values of \(x_i\) that are selected never shorten \(\tau _i\)’s virtual deadline \(x_i\cdot D_i\). As a result, we do not need to test \(\tau _i\)’s past deadlines anew. This deadline tightening technique reduces the number of possibilities for \(x_i\), but it also keeps the algorithm simple.

Computed(i) in line 11 returns ’false’, if no \(x_i\) has been computed yet for the current i, which we need to flag whether a value of \(x_i\) has been already computed for the current \(\tau _i\) or not. The function getNextDeadline() in line 15 returns the point in time t at which the next deadline occurs and the index i of the task corresponding to that deadline. Clearly, this function has to take the computed values of \(x_i\) into account.

The function testLO() succeeds if it finishes testing \(\text {dbf}_{LO}(t)\) for \(0\le t\le \max (D_{max}, \hat{t}_{LO})\)Footnote 4 and it could find a value of \(x_i\) in (0, 1] for each HI task in \(\tau\). On the other hand, testLO() fails, if \(\text {dbf}_{LO}(t)>t\) holds for some t and either t corresponds to a deadline of a LO task—whose deadline cannot be adjusted by the used tightening technique—or the resulting \(x_i\) becomes greater than 1 (lines 4 to 8).

figure c

Analogous to testLO(), testSW() computes \(\text {dbf}_{SW}(t)\) for all deadlines in the interval \(0\le t\le \max (D_{max}, \hat{t}_{SW})\) starting from \(1-x_i=1\) for all HI tasks—recall that deadlines in \(\text {dbf}_{SW}(t)\) are equal to \((1-x_i) D_i\). Otherwise, as mentioned above, testLO() and testSW() are very similar and, hence, the above explanation for testLO() also applies to testSW(). Finally, the function testHI() in Algorithm 1 is the known schedulability test for EDF from the literature (Baruah et al. 1990) and, hence, does not require further discussion.

5 Analytical comparison

In this section, let us first compare the proposed demand bound functions from Sect. 4 with those used by Ekberg and Yi in the GREEDY algorithm (Ekberg and Yi 2012) and by Easwaran in the ECDF algorithm (Easwaran 2013). We show, for most cases, that the proposed ones result in tighter bounds on the execution demand than the other mentioned approaches.

5.1 The GREEDY algorithm

In LO mode, note that \(\text {dbf}_{LO}(t)\) in (5) is identical to that of Ekberg and Yi—denoted by \({\text {gdbf}}_{LO}(t)\) in this paper. That is, \(\text {dbf}_{LO}(t)={\text {gdbf}}_{LO}(t)\) for all \(0<t\le \hat{t}_{LO}\).

In HI mode, Ekberg and Yi proposed a demand bound function—denoted \({\text {gdbf}}_{HI}(t)\) in this paper—which is given by the following expression (Ekberg and Yi 2012):

$$\begin{aligned} {\text {gdbf}}_{HI}(t)= & {} \sum \limits _{\chi _i=HI}\left( \left\lfloor \frac{t-\Delta D_i}{T_i}\right\rfloor +1\right) C_{i}^{HI}-\sum \limits _{\chi _i=HI}\text {done}_i(t), \end{aligned}$$
(13)

with \(\Delta D_i=D_i-x_i\cdot D_i\) and \(\text {done}_i(t)\) is given by:

$$\begin{aligned} \text {done}_i(t)= {\left\{ \begin{array}{ll} \max \left( 0,C_i^{LO}-\!\!\!\!\!\mod \!\!\!\left( \frac{t}{T_i}\right) +\Delta D_i\right) , \text { if } D_i>\!\!\!\!\!\!\mod \!\!\!\left( \frac{t}{T_i}\right) \ge \Delta D_i,\\ 0, \quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

Note that \({\text {gdbf}}_{HI}(t)\) bounds the execution demand in HI mode taking transitions into account. In our case, as discussed above, we derive different bounds on the execution demand at transitions and in stable HI mode, i.e., \(\text {dbf}_{SW}(t)\) and \(\text {dbf}_{HI}(t)\) respectively.

Now, since \(\text {done}_i(t)\le C_i^{LO}\) holds for all valid values of t and \(x_i\), \(\text {dbf}_{SW}(t)\le {\text {gdbf}}_{HI}(t)\) also holds for all t. In other words, if the transition to HI mode is safe by \({\text {gdbf}}_{HI}(t)\), it will also be safe by the proposed \(\text {dbf}_{SW}(t)\). However, this does not hold the other way around, i.e., \(\text {dbf}_{SW}(t)\) results in a tighter bound on the execution demand at transitions from LO to HI mode than \({\text {gdbf}}_{HI}(t)\).

On the other hand, if transitions are safe, it is guaranteed that no deadlines are missed after switching to HI mode at a \(t'\) and until the processor first idles at a \(t''\). From \(t''\) onwards, it is easy to see that our proposed \(\text {dbf}_{HI}(t)\) is sufficient and necessary. That is, if \(\text {dbf}_{HI}(t)\le t\) does not hold for some t with \(0\le t\le \hat{t}_{HI}\), then the system is not feasible, i.e., it will be neither be feasible by \({\text {gdbf}}_{HI}(t)\).

5.2 The ECDF algorithm

Similar to the case of the GREEDY algorithm, note that \(\text {dbf}_{LO}(t)\) in (5) is identical to that used in the ECDF algorithm in LO mode. We denote this latter by \({\text {edbf}}_{LO}(t)\) in this paper. That is, \(\text {dbf}_{LO}(t)={\text {edbf}}_{LO}(t)\) for all \(0<t\le \hat{t}_{LO}\).

In HI mode, the ECDF algorithm uses a demand bound function—denoted \({\text {edbf}}_{HI}(t)\) in this paper—which is given by the following expression (Easwaran 2013):

$$\begin{aligned} {\text {edbf}}_{HI}(t_1,t_2)= & {} \min \left( t_1,\sum \limits _{j=1}^3\text {dbf}_{L_j}(t_1,t_2)\right) \nonumber \\&+\sum \limits _{\begin{array}{c} \chi _i=HI \\ \text {and case 2 or 3} \end{array}}\!\!\text {dbf}^{HI}_i(t_1,t_2)\nonumber \\&+\sum \limits _{\begin{array}{c} \chi _i=HI \\ \text {and case 2} \end{array}}\!\!\left( CO(t_2-t_1)+\Delta C_{i}\right) , \end{aligned}$$
(14)

where \(\Delta C_i\) is defined as \(C_{i}^{HI}-C_{i}^{LO}\). In addition, \(0\le t_2\le \hat{t}_{HI}\) and \(0\le t_1\le t_2-\min \limits _{\chi _i=HI}\left( \Delta D_i\right)\) hold with again \(\Delta D_i=D_i-x_i\cdot D_i\).

Here \(t_1\) represents the point in time at which the system switches to HI mode (i.e., \(t_1=t'\) in our notation) and \(t_2\) is the point in time at which a deadline is potentially missed (i.e., \(t_2=t_{miss}\le t''\) in this paper). Note that \(\text {dbf}^{HI}_i(\cdot )\) is a \(\tau _i\)’s contribution to \(\text {dbf}_{HI}(\cdot )\) shown in (8). HI tasks in (14) are classified into three cases: case 1 which plays a role in computing \(\text {dbf}_{L_j}(\cdot )\), case 2, and case 3. For details on how to compute \(\text {dbf}_{L_j}(\cdot )\) for \(1\le j\le 3\) and how to compute \(CO(\cdot )\) we refer to Easwaran (2013).

The system is schedulable in HI mode, if \({\text {edbf}}_{HI}(t_1,t_2)\le t_2\) holds. (Here again no distinction is made between transition and stable HI mode.) Let us now consider that \(t_1\) is less than or equal to \(\sum _{j=1}^3\text {dbf}_{L_j}(t_1,t_2)\), such that the schedulability condition by ECDF now becomes:

$$\begin{aligned}&\sum \limits _{\begin{array}{c} \chi _i=HI \\ \text {and case 2 or 3} \end{array}}\!\!\text {dbf}^{HI}_i(t_1,t_2)+\sum \limits _{\begin{array}{c} \chi _i=HI \\ \text {and case 2} \end{array}}\!\!\left( CO(t_2-t_1)+\Delta C_{i}\right) \le t_2-t_1. \end{aligned}$$
(15)

Easwaran proved that the left-hand side of the above condition is equal to \({\text {gdbf}}_{HI}(t_2-t_1)\) (Easwaran 2013). As a consequence, the proposed \(\text {dbf}_{SW}(t)\) results in a tighter bound than (15), since \(\text {dbf}_{SW}(t)\le {\text {gdbf}}_{HI}(t)\) holds for all t—see again the above Sect. 5.1.

In the case where \(t_1\) is greater than \(\sum _{j=1}^3\text {dbf}_{L_j}(t_1,t_2)\), the analytical comparison between \({\text {edbf}}_{HI}(\cdot )\) and \(\text {dbf}_{SW}(\cdot )\) becomes difficult. This is the case where some amount of the execution demand given by \({\text {edbf}}_{HI}(\cdot )\) starts being executed before \(t_1\), at \(t_1-\sum _{j=1}^3\text {dbf}_{L_j}(t_1,t_2)\) to be more precise. Whether a proof of dominance exists (in either way) remains an open problem.

At least, from the above discussion, we can assert that the proposed \(\text {dbf}_{SW}(\cdot )\) is tighter for the more stringent case, i.e., when no execution demand by \({\text {edbf}}_{HI}(\cdot )\) can be executed before \(t_1\). Our experiments in the following section present evidence that this also holds on average, i.e., \(\text {dbf}_{SW}(\cdot )\) usually results in tighter bounds, particularly, when the number of HI task increases.

6 Applying approximation techniques

In this section, we apply approximation techniques, particularly, Devi’s test (Devi 2003) to derive two variants of the proposed approach trading off accuracy for the sake of lesser complexity/runtime. The first variant computes one deadline scaling factor per HI task, similar to the proposed approach, but with less accuracy to reduce complexity. In contrast to it, the second variant computes only one deadline scaling factor for all HI tasks requiring, in principle, less computation. However, as discussed later in detail, this does not necessarily lead to a lower complexity.

6.1 Revisiting Devi’s test

Let us consider a set \(\bar{\tau }\) of non-MC tasks that are independent, preemptable and sporadic. Similar to tasks in \(\tau\) defined in Sect. 3, each individual \(\tau _i\) in \(\bar{\tau }\) is defined by its minimum inter-release time \(T_i\) and its relative deadline \(D_i\) being \(D_i \le T_i\). However, in contrast to tasks in \(\tau\), tasks in \(\bar{\tau }\) are characterized by only one WCET parameter denoted by \(C_i\).

In addition, let us assume that tasks in \(\bar{\tau }\) are sorted in the order of non-decreasing deadlines, i.e., \(D_i\le D_j\) holds, if \(i<j\) holds where i and j are indices identifying tasks. Devi’s test states that \(\bar{\tau }\) is feasible on one processor under preemptive EDF scheduling, if the following condition holds for \(1\le k \le |\bar{\tau }|\) (where \(|\bar{\tau }|\) denotes the number of tasks in \(\bar{\tau }\)) (Devi 2003):

$$\begin{aligned} \sum _{i=1}^{k}\frac{C_i}{T_i}+\frac{1}{D_k}\left( \sum \limits _{i=1}^{k}\frac{T_i-D_i}{T_i} C_i \right) \le 1, \end{aligned}$$
(16)

resulting in a sufficient, but not necessary test with polynomial complexity. As opposed to it, an exact test for \(\bar{\tau }\)—based on the concept of demand bound function—leads to a higher, pseudo-polynomial complexity (Baruah et al. 1990).

6.2 Per-task deadline scaling

We can now derive the first approximated variant of our proposed approach computing a scaling factor for each individual HI task in \(\tau\). To this end, we use Devi’s test to analyze each mode and the transition between them.

6.2.1 Schedulability in LO mode

When applying Devi’s test in LO mode, the demand bound function in (5) reduces to the following condition:

$$\begin{aligned}&\sum _{i=1}^{k}\frac{C_i^{LO}}{T_i}+\frac{1}{x_k\cdot D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{LO}\right. \nonumber \\&\left. +\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{T_i-x_i\cdot D_i}{T_i} C_i^{LO}\right) \le 1, \end{aligned}$$
(17)

where \(1\le k\le |\tau |\) and \(|\tau |\) denotes the total number of tasks in \(\tau\). Tasks in (17) need to be sorted in order of non-decreasing real deadlines \(D_i\) for \(\chi _i=LO\) or virtual deadlines \(x_i\cdot D_i\) for \(\chi _i=HI\). Note that the order of tasks might change depending on the values of \(x_i\). As a result, (17) might need to be recomputed for the corresponding tasks, if their relative order changes.

Further, in (17), we have considered that the current \(\tau _k\) (i.e., for the current value of k) is a HI task. As a result, a deadline scaling factor \(x_k\) needs to be computed. If \(\tau _k\) is a LO task, the second term of (17) is divided by \(D_k\) instead of \(x_k\cdot D_k\), since LO tasks are scheduled within their real deadlines. In this case, no \(x_k\) needs to be computed.

6.2.2 Schedulability in stable HI mode

Now, when applying Devi’s test in HI mode, the demand bound function in (8) reduces to the following condition:

$$\begin{aligned} \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{C_i^{HI}}{T_i}+\frac{1}{D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{HI}\right) \le 1, \end{aligned}$$
(18)

where again \(1\le k\le |\tau |\) holds. Note that only HI tasks are considered in (18), which need to be sorted in order of non-decreasing \(D_i\).

6.2.3 Schedulability in the transition from LO to HI mode

The demand bound function in (10) reduces to the following condition after applying Devi’s test:

$$\begin{aligned} \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{\Delta C_i}{T_i}+\frac{1}{(1-x_k) D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{T_i-\Delta D_i}{T_i} \Delta C_i\right) \le 1, \end{aligned}$$
(19)

with \(1\le k\le |\tau |\) as before, \(\Delta C_i=C_i^{HI}-C_i^{LO}\), and \(\Delta D_i=(1-x_i) D_i\). Similar to stable HI mode, only HI tasks are considered in (19). However, this time, tasks are sorted in the order of non-decreasing \(\Delta D_i\) instead. Similar to the LO mode, the order of tasks might change depending on the values of \(x_i\). In this case, (19) needs to be recomputed for all tasks whose relative order changes for a newly computed \(x_k\).

6.2.4 Finding deadline scaling factors

As already discussed, (17) needs to hold for all k in \(1\le k\le |\tau |\), which is tested in an iterative manner. Clearly, \(x_k\) only needs to be computed for \(\chi _k=HI\). To this end, let us first reshape (17) to the following:

$$\begin{aligned}&\sum _{i=1}^{k}\frac{C_i^{LO}}{T_i}+\frac{1}{x_k\cdot D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{LO}\right. \nonumber \\&\left. +\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k-1}\frac{T_i-x_i\cdot D_i}{T_i} C_i^{LO}+\frac{T_k-x_k\cdot D_k}{T_k} C_k^{LO}\right) \le 1, \end{aligned}$$

which we can then solve for \(x_k\) leading to:

$$\begin{aligned} \frac{\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{LO}+\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k-1} \frac{T_i-x_i\cdot D_i}{T_i} C_i^{LO}+C_k^{LO}}{D_k\left( 1-\sum _{i=1}^{k}\frac{C_i^{LO}}{T_i}\right) +D_k\frac{C_k^{LO}}{T_k}}\le x_k. \end{aligned}$$

Note that we can change the upper limit of the first summation in the numerator to \(k-1\), since \(\chi _k=HI\) holds. Further, reshaping the denominator, we finally obtain:

$$\begin{aligned} \frac{\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k-1}\frac{T_i-D_i}{T_i} C_i^{LO}+\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k-1} \frac{T_i-x_i\cdot D_i}{T_i} C_i^{LO}+C_k^{LO}}{D_k\left( 1-\sum _{i=1}^{k-1}\frac{C_i^{LO}}{T_i}\right) }\le x_k. \end{aligned}$$
(20)

As already mentioned, we might need to recompute (17) for all tasks whose relative order changes depending on the value of \(x_k\). To avoid this complication, we derive the following lower bound for \(x_k\):

$$\begin{aligned} \frac{D_{k-1}^{LO}}{D_k}\le x_k, \end{aligned}$$
(21)

where \(D_{k-1}^{LO}=D_{k-1}\) or \(D_{k-1}^{LO}=x_{k-1}\cdot D_{k-1}\) depending on whether \(\chi _{k-1}=LO\) or \(\chi _{k-1}=HI\) respectively. In words, (21) guarantees that the selected \(x_k\) does not change the order of tasks in LO mode to avoid having to recompute (17), clearly, at the cost of a lesser accuracy.

Now, we can obtain an upper bound on \(x_k\) reshaping (19) to:

$$\begin{aligned} \sum _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{\Delta C_i}{T_i}+\frac{1}{(1-x_k) D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k-1}\frac{T_i-\Delta D_i}{T_i} \Delta C_i+\frac{T_k-(1-x_k) D_k}{T_k} \Delta C_k\right)\le & {} 1. \end{aligned}$$

Solving for \(1-x_k\) and reshaping as before, we obtain:

$$\begin{aligned} 1-\frac{\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k-1} \frac{T_i-\Delta D_i}{T_i} \Delta C_i+\Delta C_k}{D_k\left( 1-\sum _{i=1}^{k-1}\frac{\Delta C_i}{T_i}\right) }\ge x_k. \end{aligned}$$
(22)

Similar to before, to avoid having to recompute (19), we need to prevent that the order of tasks changes, for which we derive the following upper bound on \(x_k\):

$$\begin{aligned} 1-\frac{(1-x_{k-1}) D_{k-1}}{D_k}\ge x_k. \end{aligned}$$
(23)

Finally, a system is feasible under mixed-criticality EDF, if (17) holds for all k and (18) holds for all k with \(\chi _k=HI\). In addition, we need to find a valid \(x_k\) for every \(\tau _k\) with \(\chi _k=HI\). That is, \(x_k\) must be greater than or equal to the maximum between (20) and (21). Simultaneously, \(x_k\) must be less than or equal to the minimum between (22) and (23).

6.3 Uniform deadline scaling

We can also apply Devi’s test to derive a second approximated variant of our proposed approach, computing only one deadline scaling factor for all HI tasks in \(\tau\). In principle, this requires less computation than our first approximated variant. However, in contrast to what is expected, this second variant does not result in a lower complexity, since it cannot prevent the order of tasks from changing as discussed below.

6.3.1 Schedulability in LO mode

We again apply Devi’s test to the demand bound function in (5), but considering this time a uniform deadline scaling factor x:

$$\begin{aligned} \sum _{i=1}^{k}\frac{C_i^{LO}}{T_i}+\frac{1}{x\cdot D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{LO}\right. \nonumber \\ \qquad \left. +\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{T_i-x\cdot D_i}{T_i} C_i^{LO}\right) \le 1, \end{aligned}$$
(24)

where \(1\le k\le |\tau |\) and \(|\tau |\) denote the total number of tasks in \(\tau\). Just as before, tasks in (24) need to be sorted in order of non-decreasing real deadlines \(D_i\) for \(\chi _i=LO\) or virtual deadlines \(x\cdot D_i\) for \(\chi _i=HI\). Although the relative order of HI tasks (among themselves) never changes, the order of LO tasks with respect to HI tasks might still change for some x. If that happens, (24) needs to be recomputed for the corresponding tasks.

In (24), note that the current \(\tau _k\) is considered to be a HI task and, hence, x needs to be computed. If \(\tau _k\) is a LO task, the second term of (24) is divided by \(D_k\) instead of \(x\cdot D_k\), since LO tasks are scheduled within their real deadline. In this case, no x is computed; however, (24) still needs to hold for the previously selected x.

6.3.2 Schedulability in stable HI mode

When considering a uniform deadline scaling factor x, we still obtain (18) as a result of applying Devi’s test to (9). Hence, this case requires no further discussion.

6.3.3 Schedulability in the transition from LO to HI mode

The demand bound function in (11) reduces to the following condition after applying Devi’s test for a uniform deadline scaling factor x:

$$\begin{aligned} \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{\Delta C_i}{T_i}+\frac{1}{(1-x) D_k}\left( \sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{T_i-(1-x) D_i}{T_i} \Delta C_i\right) \le 1, \end{aligned}$$
(25)

with \(1\le k\le |\tau |\), and \(\Delta C_i\) is defined as before. Only HI task are considered in (25) and tasks are sorted in the order of non-decreasing \((1-x) D_i\). This time, however, the order of tasks cannot change for different values of x, since x affects all deadlines the same.

6.3.4 Finding a uniform deadline scaling factor

Proceeding as before, we can obtain a lower bound on x from (24):

$$\begin{aligned} \frac{\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=LO \end{array}}^{k}\frac{T_i-D_i}{T_i} C_i^{LO}+\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k} C_i^{LO}}{D_k\left( 1-\sum _{i=1}^{k}\frac{C_i^{LO}}{T_i}\right) +\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}D_i \frac{C_i^{LO}}{T_i}}\le x. \end{aligned}$$
(26)

Note that the order between some HI and LO tasks might change for a given x, requiring us to recompute (24). As mentioned above, in contrast to the per-task deadline scaling, it becomes difficult to derive an additional lower bound on x that prevents this from happening. We can, of course, select an x for the current \(\tau _k\) such that \(D_{k-1}^{LO}\le x\cdot D_{k}\) holds, where \(D_{k-1}^{LO}\) represents \(\tau _{k-1}\)’s deadline in LO mode (independent of whether this is a LO or HI task). However, this is not sufficient, since a new value of x also affects all previously tested HI tasks, whose deadlines might become smaller than some deadline of a LO task.

An upper bound on x can be obtained from (25), which leads to:

$$\begin{aligned} x\le 1-\frac{\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k} \Delta C_i}{D_k\left( 1-\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}\frac{\Delta C_i}{T_i}\right) +\sum \limits _{\begin{array}{c} i=1 \\ \chi _i=HI \end{array}}^{k}D_i \frac{\Delta C_i}{T_i}}. \end{aligned}$$
(27)

According to this second variant of our proposed approach, the system is feasible under mixed-criticality EDF, if (24) holds for all k and (18) holds for all k with \(\chi _k=HI\). In addition, none of the values of x obtained with (27) should be less than any value obtained by (26) for \(1\le k\le |\tau |\) with \(\chi _k=HI\).

6.4 Complexity

Similar to GREEDY (Ekberg and Yi 2012) and ECDF (Easwaran 2013), the proposed approach of Sect. 4 is based on computing demand bound functions and, hence, has a pseudo-polynomial complexity \(\mathcal {O}(K_n\cdot n)\) for task sets with a total utilization that is strictly less than 1 (Baruah et al. 1990). Note that n represents the number of tasks in the given task set and \(K_n\) is a factor that depends on task parameters and, therefore, on n. In contrast to this, EDF-VD (Baruah et al. 2012) has a linear complexity \(\mathcal {O}(n)\).

The approximated variant in Sect. 6.2, based on computing per-task deadline scaling factors, has a polynomial complexity \(\mathcal {O}(n\cdot \log n)\), when the bounds in (21) and (23) are considered. As explained above, these prevent that the order of tasks changes for a newly computed deadline scaling factor. If (21) and (23) are not considered, the order of tasks might change requiring us to retest some of the (previously tested) tasks and, hence, leading to a quadratic complexity \(\mathcal {O}(n^2)\) instead.

On the other hand, the complexity of our second approximated variant of Sect. 6.7 is quadratic \(\mathcal {O}(n^2)\), since, in the general case, i.e., with at least one LO task in the system, it cannot guarantee that the order of tasks does not change. As a result, retesting cannot be avoided.

7 Experimental evaluation

In this section, we present evaluation results based on synthetic data. The intention is to show how the different algorithms behave with respect to each other and not to provide any absolute performance metrics.

In particular, we compare the proposed approach of Sect. 4 with EDF-VD (Baruah et al. 2012), with the GREEDY algorithm by Ekberg and Yi (2012), and with ECDF by Easwaran (2013). Note that we had to modify EDF-VD to consider the deadlines \(D_i\) of tasks instead of their inter-arrival times or periods \(T_i\), i.e., to consider the tasks’ densities instead of their utilizations, to account for the case of constrained deadlines \(D_i\le T_i\) and be compared with the other algorithms in a meaningful manner.

In addition, we include our first approximated variant from Sect. 6.2 in this comparison. As discussed in Sect. 6.12, this is the one with the lowest complexity and helps illustrating how much performance can be attained with the proposed technique at the least possible cost.

7.1 Schedulability curves

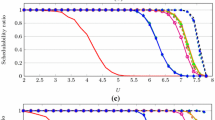
Figure 3 shows schedulability curves, i.e., the percentage of feasible task sets by the above algorithms, versus LO utilization. For every increase in LO utilization, a total number of 1000 different sets of 20 tasks each were randomly generated—\(10,\!000\) task sets in total. We made use of UUniFast (Bini and Buttazzo 2005) to generate individual task utilizations.

Further, we used the log-uniform distribution proposed by Emberson et al. (2010) to create the task periods \(T_i\) in the range of 1–1000 ms. The log-uniform distribution guarantees that task periods are equally spread into the time bands 1–10 ms, 10–100 ms, etc.

With \(T_i\) and the task utilization, we obtained the values of \(C_i^{LO}\). We assumed that \(30\%\) of the tasks are HI tasks, i.e., 6 out of 20 tasks. Further, for each HI task, we randomly selected an increase in HI execution demand of at most \(50\%\) of \(\frac{C_i^{LO}}{T_i}\). With this, we then obtained the values of \(C_i^{HI}\). Deadlines \(D_i\) are constrained and chosen from a uniform distribution in the range \([C_i^{HI}, T_i]\) for HI tasks and in \([C_i^{LO}, T_i]\) for LO tasks.

As depicted in Fig. 3, expectedly, the percentage of schedulable task sets decreases with an increasing LO utilization. On the other hand, whereas all algorithms perform similarly for a LO utilization below \(50\%\), they exhibit different behaviors for higher LO utilizations. In particular, the proposed approach outperforms ECDF by around 10–\(20\%\) more accepted task sets in the range of 60 to \(100\%\) LO utilization. Interestingly, in spite of having a lesser complexity, our approximated variant shows a similar performance to the GREEDY algorithm.

Fig. 3
figure 3

Schedulability versus LO utilization for \(|\tau |=20\), \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

7.2 Weighted schedulability

Next, we make use of the concept of weighted schedulability (Bastoni et al. 2010; Davis 2016) to analyze the performance by the above algorithms. That is, for a schedulability test A whose accuracy on testing a task set \(\tau\) is a function of parameter p, its weighted schedulability \(W_A(p)\) is given by:

$$\begin{aligned} \text{ W}_{A}(p)= & {} \frac{\sum \limits _{\begin{array}{c} \forall \tau \end{array}} U(\tau ) \cdot \text {S}_A(\tau ,p)}{\sum \limits _{\begin{array}{c} \forall \tau \end{array}} U(\tau )}, \end{aligned}$$
(28)

where \(\text {U}(\tau )\) is the utilization of a given \(\tau\) and \(S_A(\tau ,p)\) is A’s binary result (1 if schedulable and 0 if not) for a task set \(\tau\) with parameter value p. In other words, individual schedulability results by A are weighted according to the utilization of the task sets tested, putting more emphasis on higher-utilization ones.

We created weighted schedulability curves varying following parameters: (i) total number of tasks, (ii) percentage of HI tasks, (iii) increase of HI execution demand and (iv) range of task periods. Every time we varied one of these parameters, we generated 1000 different task sets for each LO utilization value between 0 and \(100\%\) at steps of \(10\%\), i.e., a total of \(10,\!000\) task sets per marker on the shown curves. To this end, we proceeded as described previously to obtain task parameters.

Fig. 4
figure 4

Weighted schedulability versus total number of tasks for \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

Figure 4 shows weighted schedulability curves for a varying total number of tasks where we selected the number of HI tasks to be equal to \(30\%\) of the total (i.e., it also varies proportionally) and the increase of HI execution demand to be \(50\%\) of the LO execution demand for each HI task. The proposed approach outperforms all other algorithms by around 10–\(20\%\) depending on the total number of tasks. In general, the more the tasks, the better the proposed algorithm performs with respect to the others. It is interesting to note that ECDF performs better than GREEDY up to 30 tasks per set, after which GREEDY performs better. Further, ECDF seems to stagnate at around \(80\%\) weighted schedulability, in contrast to GREEDY and the proposed approach.

Our approximated variant has a good performance up to around 40 tasks, after which it decays pronouncedly, even becoming worse than EDF-VD from 80 tasks onwards. The reason is that this algorithm is based on Devi’s test, which requires tasks to be sorted by deadline. Since the order of tasks may change with every new deadline scaling factor, some tasks may need to be retested as explained in Sect. 6.2. Clearly, the more tasks there are, the more likely it is that their order changes (when scaling one deadline). To avoid this and reduce complexity, we introduced conditions (21) and (23), which truncate the valid range of deadline scaling factors. This has the downside, however, that the number of wrongly rejected task sets increases disproportionally as the total number of tasks grows.

Fig. 5
figure 5

Weighted schedulability versus percentage of HI tasks for \(|\tau |=20\) and \(50\%\) increase of HI execution demand

Full size image

Weighted schedulability curves for a varying percentage of HI tasks are shown in Fig. 5. This time, we selected the total number of tasks to be 20, whereas the increase of HI execution demand continues to be \(50\%\) as in the previous case. We can see that the performance of all approaches decreases with an increasing number of HI tasks. Up to around \(20\%\) HI tasks (i.e., 4 out of 20), the proposed approach and ECDF behave similarly. However, ECDF’s performance then decreases rapidly, becoming worse than GREEDY and even EDF-VD at \(50\%\) and \(60\%\) HI tasks respectively.

At around \(80\%\) HI tasks (16 out of 20 tasks), the proposed approach still allows for around \(80\%\) schedulable task sets independent of the LO utilization, whereas all other algorithms are at or below \(40\%\) schedulable task sets. This evidences the effectiveness of the proposed approach over GREEDY and ECDF for general cases. In particular, GREEDY and ECDF are based on estimating the worst-case contributions by carry-over jobs at the moment of switching from LO to HI mode. This inevitably becomes pessimistic as the number of carry-over jobs grows, which directly depends on the number of HI tasks.

In the case of our approximated variant, again, conditions (21) and (23) start dominating in Fig. 5. Even though the total number of tasks remains constant, these two conditions are evaluated for each HI task. As a result, if the number of HI tasks increases, they start playing a bigger role and, hence, accentuating the decrease in performance.

Fig. 6
figure 6

Weighted schedulability versus increase of HI execution demand for \(|\tau |=20\) and \(30\%\) HI tasks

Full size image

In Fig. 6, we further present weighted schedulability curves for a varying increase of HI execution demand. We again selected the total number of tasks to be 20 and the number of HI tasks is set to \(30\%\). In this case, the behavior of algorithms slightly worsens for a growing HI execution demand with exception of ECDF, whose behavior slightly improves. In spite of this, the proposed algorithm outperforms all others by around \(10\%\) more schedulable task sets in the range of 10–\(80\%\) increase in HI execution demand. Interestingly, our approximated variant also shows a good performance in this range, which is even better than that of the GREEDY algorithm up to \(60\%\) increase in HI execution demand.

Fig. 7
figure 7

Weighted schedulability versus range of task periods for \(|\tau |=20\), \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

Last, Fig. 7 shows weighted schedulability curves for a varying range of task periods with the total number of tasks being again 20, out of which \(30\%\) are HI tasks with a \(50\%\) increase in HI execution demand. In this case, the performance of all algorithms rapidly goes down for an increasing range of task periods. The proposed approach outperforms ECDF by 10–\(20\%\) more schedulable task sets when the minimum and the maximum task period are 3 to 4 orders of magnitude apart. Note that our approximated variant outperforms GREEDY for period ranges of 2.5 orders of magnitude upwards and has a comparable performance to that of ECDF between 3.5 to 4 orders of magnitude.

Fig. 8
figure 8

Runtime versus LO utilization for \(|\tau |=20\), \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

7.3 Runtime comparison

Figures 8 to 10 show a comparison of runtime versus LO utilization, total number of tasks and range of task periods respectively. However, note that we have implemented the different algorithms in Matlab and, hence, they can be further optimized, potentially changing their behavior with respect to runtime.

Now, ECDF is around one to two orders of magnitude faster than GREEDY and the proposed approach depending on LO utilization as shown in Fig. 8. Our approximated variant is around one order of magnitude slower than EDF-VD and around one to two orders of magnitude faster than ECDF. This behavior remains almost unchanged as the number of tasks increases towards 100 tasks per set—see Fig. 9. Here we maintained the percentage of HI tasks and the increase of HI execution demand equal to \(30\%\) and \(50\%\) respectively. Only for 10 tasks per set, GREEDY and the proposed algorithm are as fast as ECDF.

Fig. 9
figure 9

Runtime versus total number of tasks for \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

Figure 10 shows runtime curves for an increasing range of task periods. We again kept the total number of tasks at 20, the percentage of HI tasks at \(30\%\) and the increase of HI execution demand at \(50\%\). As expected, our approximated variant and EDF-VD have a constant runtime for an increasing range of periods, since both have polynomial complexity. All other algorithms experience an increasing runtime for greater period ranges. ECDF continues to be around one order of magnitude faster than GREEDY and the proposed algorithm. However, this difference reduces as the range of task periods grows. At 4 orders of magnitude between the minimum and the maximum period, all these algorithms show the same runtime.

It should be noted that Figs. 9 and 10 are independent of LO utilization. For each marker on these curves, we generated 1000 different task sets for each LO utilization value between 0 and \(100\%\) at steps of \(10\%\), i.e., a total of \(10,\!000\) task sets per marker.

Fig. 10
figure 10

Runtime versus range of task periods for \(|\tau |=20\), \(30\%\) HI tasks and \(50\%\) increase of HI execution demand

Full size image

8 Concluding remarks

In this paper, we studied the problem of mixed-criticality scheduling under EDF, where a set of low-criticality (LO) and high-criticality (HI) tasks share the processor. Similar to the literature, we characterize execution demand in a mixed-criticality task set by deriving demand bound functions in the different operation modes, i.e., HI and LO mode. Particularly, we handle transitions from LO to HI mode separately from the stable HI mode, which allows us to work around carry-over jobs and, therefore, to reduce pessimism in estimating execution demand under mixed-criticality EDF.

It is interesting to notice that the proposed approach reduces the problem of testing schedulability under mixed-criticality EDF to testing schedulability of three almost unrelated task sets: the one in LO mode, the one in HI mode and the equivalent task set for transitions between LO and HI mode. This allows applying well-known approximation techniques that trade off accuracy for the sake of a lesser complexity/runtime as illustrated for the case of Devi’s test.

Further, we conducted a large set of experiments on synthetic data showing the effectiveness of the proposed approach and of its approximated variant in terms of (weighted) schedulability and runtime respectively. This is particularly notable as the number of HI tasks increases.

Which algorithm should be used depends very much on the context. If we are testing offline, we believe, there is no harm in using all three algorithms (GREEDY, ECDF and the proposed test). If tests are to be performed online, it is probably better to used the approximated variant of the proposed test—with a \(\mathcal {O}(n\cdot \log n)\) rather than pseudo-polynomial complexity.

Finally, in the appendix, we show how to extend the proposed approach to more than two levels of criticality considering ordered (i.e., where criticality levels cannot be skipped) and unordered modes switches.