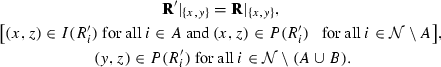Abstract
This paper examines social choice theory with the strong Pareto principle. The notion of conditional decisiveness is introduced to clarify the underlying power structure behind strongly Paretian aggregation rules satisfying binary independence. We discuss the various degrees of social rationality: transitivity, semi-transitivity, the interval-order property, quasi-transitivity, and acyclicity.
Similar content being viewed by others
Notes
Cato (2011) provides sufficient conditions for the equivalence between the weak Pareto and strong Pareto principles.
An exception is the maximin criterion. Sen (1970) proposes a lexicographic refinement of the maximin criterion.
Arrow’s theorem does not hold in the case of an infinite population. See Fishburn (1970).
Campbell and Kelly (2002) provide a survey of Arrovian social choice theory.
Another expression is as follows: there exists a permutation \(\rho :\mathcal{N } \rightarrow \mathcal{N }\) such that for all \(i\), if \((x,y)\in P(R_i)\) and there exists no \(j\) such that \(\rho (j)<\rho (i)\) and \((y,x)\in P(R_j)\), then \((x,y)\in P(W(\mathbf{R}))\).
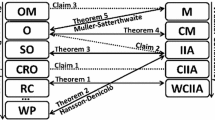
Similarly, the structure of \(\mathcal{N }\) is unspecified in later theorems (Theorems 2– 5), and subsequent discussions are only sketches of the finite case.
Some might consider our definition of the serial oligarchy to be weak. An alternative definition is as follows: there exists a partition \((B_1,\dots ,B_K)\) such that for all \(k\), if \((x,y)\in P(\bigcap _{i \in B_k}R_i)\) and \((x,y)\in \bigcap _{i \in C_{k}}I(R_i)\), then \((x,y)\in P(W(\mathbf{R}))\). This definition is natural, but it is not equivalent to the filter structure of the conditionally decisive sets.
Similar to the serial oligarchy, the serial collegium provides only a partial description of the collective process; there are many SDFs with the same structure of the serial collegium.
The proof of the theorem is as follows. Condition (i) immediately follows from strong Pareto. If condition (ii) is violated, \((x,y) \in P(W(\mathbf{R}))\) and \((y,x) \in P(W(\mathbf{R}))\) whenever \((x,y) \in \bigcap _{i \in M \cap M^{\prime }} I(R_i),\,(x,y) \in \bigcap _{i \in M - M^{\prime }} P(R_i)\), and \((y,x) \in \bigcap _{i \in M^{\prime } - M} P(R_i)\).
An exception is Theorem 5. In the theorem, binary independence is not required to be satisfied, but acyclicity of social preference has a critical role for the consequence.
In the rest of this section, we assume that both \(\mathcal{N }\) and \(X\) are finite.
The above-mentioned rule generates Suzumura-consistent social preferences. A binary relation is Suzumura-consistent if and only if, for all \(K \in \mathbb{N }\) and for all \(x^0, \dots , x^K,\,(x^{k-1},x^k) \in R \ \forall k \in \{1,\dots , K\} \Rightarrow (x^K,x^0) \notin P(R)\). The concept is proposed by Suzumura (1976); Bossert and Suzumura (2008)) characterize a class of CCRs generating Suzumura-consistent social preferences. See Bossert and Suzumura (2010) for a comprehensive argument.
They also imposed the axiom of stationarity on CCRs.
References
Aliprantis, C. D., & Border, K. C. (2006). Infinite dimensional analysis: A hitchhiker’s guide. Berlin: Springer Verlag.
Arrow, K. J. (1951). Social choice and individual values (2nd ed., 1963). New York: Wiley.
Banks, J. S. (1995). Acyclic social choice from finite sets. Social Choice and Welfare, 12, 293–310.
Blair, D. H., Bordes, G., Kelly, J. S., & Suzumura, K. (1975). Impossibility theorems without collective rationality. Journal of Economic Theory, 13, 361–379.
Blair, D. H., & Pollak, R. A. (1979). Collective rationality and dictatorship: The scope of the Arrow theorem. Journal of Economic Theory, 21, 186–194.
Blau, J. H. (1979). Semiorders and collective choice. Journal of Economic Theory, 21, 195–206.
Bossert, W., & Suzumura, K. (2008). A characterization of consistent collective choice rules. Journal of Economic Theory, 138, 311–320.
Bossert, W., & Suzumura, K. (2009). Decisive coalitions and coherence properties. CIREQ: Discussion Paper, Université de Montréal.
Bossert, W., & Suzumura, K. (2010). Consistency, choice and rationality. Cambridge: Harvard University Press.
Bossert, W., & Suzumura, K. (2011). Multi-profile intergenerational social choice. Social Choice and Welfare, 37, 493–509.
Brown, D. J. (1974). An approximate solution to Arrow’s problem. Journal of Economic Theory, 9, 375–383.
Brown, D. J. (1975). Aggregation of preferences. Quarterly Journal of Economics, 89, 456–469.
Campbell, K., & Kelly, J. S. (2002). Impossibility theorems in the Arrovian framework. In K. J. Arrow, A. K. Sen, & K. Suzumura (Eds.), Handbook of social choice and welfare (Vol. 1, pp. 35–94). North-Holland: Amsterdam.
Cato, S. (2011). Pareto principles, positive responsiveness, and majority decisions. Theory and Decision, 71, 503–518.
Cato, S. (2012a). Quasi-decisiveness, quasi-ultrafilter, and social quasi-orderings. Social Choice and Welfare. doi:10.1007/s00355-012-0677-z.
Cato, S. (2012b). Social choice without the Pareto principle: A comprehensive analysis. Social Choice and Welfare, 39, 869–889.
Cato, S. (2013). Remarks on Suzumura consistent collective choice rules. Mathematical Social Sciences, 65, 40–47.
Cato, S., & Hirata, D. (2010). Collective choice rules and collective rationality: A unified method of characterizations. Social Choice and Welfare, 34, 611–630.
Ferejohn, J., & Page, T. (1978). On the foundations of intertemporal choice. American Journal of Agricultural Economics, 60, 269–275.
Fishburn, P. C. (1970). Arrow’s impossibility theorem: Concise proof and infinite voters. Journal of Economic Theory, 2, 103–106.
Fishburn, P. C. (1975). Axioms for lexicographic preferences. Review of Economic Studies, 42, 415–419.
Gibbard, A. (1969). Social choice and the Arrow condition. Unpublished paper.
Guha, A. (1972). Neutrality, monotonicity, and the right of veto. Econometrica, 40, 821–826.
Hansson, B. (1976). The existence of group preference functions. Public Choice, 28, 89–98.
Kirman, A. P., & Sondermann, D. (1972). Arrow’s theorem, many agents, and invisible dictators. Journal of Economic Theory, 5, 267–277.
Mas-Colell, A., & Sonnenschein, H. (1972). General possibility theorems for group decisions. Review of Economic Studies, 39, 185–192.
Packel, E. W. (1980). Impossibility results in the axiomatic theory of intertemporal choice. Public Choice, 35, 219–227.
Packel, E. W. (1981). Social decision functions and strongly decisive sets. Review of Economic Studies, 48, 343–349.
Sen, A. K. (1969). Quasi-transitivity, rational choice and collective decisions. Review of Economic Studies, 36, 381–393.
Sen, A. K. (1970). Collective choice and social welfare. San Francisco: Holden-Day.
Suzumura, K. (1976). Remarks on the theory of collective choice. Economica, 43, 381–390.
Willard, S. (1970). General topology. Reading: Addison-Wesley Publishing Company.
Acknowledgments
I thank Tomoki Inoue and an anonymous referee of this journal for constructive suggestions. This paper was financially supported by Grant-in-Aid for Young Scientists (B) from the Japan Society for the Promotion of Science and the Ministry of Education, Culture, Sports, Science and Technology.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs
Appendix: Proofs
Lemma 1
Let \(W\) be a QSDF satisfying strong Pareto and binary independence, and let \(A \subsetneq \mathcal{N }\). If \(B \subseteq \mathcal{N } \setminus A\) is \(A\)-conditionally decisive over some pair \((x,y)\) for \(W\), then it is \(A\)-conditionally decisive for \(W\).
Proof
Let \(W\) be a QSDF satisfying strong Pareto and binary independence, and let \(A \subsetneq \mathcal{N }\). Suppose that \(B \subseteq \mathcal{N } \setminus A\) is \(A\)-conditionally decisive over \((x,y)\) for \(W\). We first prove the following claim.
Claim
For all \(z \in X,\,B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\).
Let \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) be such that
Since \(B\) is \(A\)-conditionally decisive over \((x,y)\) for \(W\), we have \((x,y) \in P(W(\mathbf{R}))\). Strong Pareto implies that \((y,z) \in P(W(\mathbf{R}))\). By quasi-transitivity, \((x,z) \in P(W(\mathbf{R}))\). The preferences of individuals outside of \(B \cup A\) over \(x\) and \(z\) are not specified, and thus, binary independence implies that \(B\) is \(A\)-conditionally decisive over \((x,z)\) for \(W\). Hence, for all \(z \in X,\,B\) is \(A\)-conditionally decisive over \((x,z)\) for \(W\).
Let \(\mathbf{R}^{\prime } \in \mathcal{R }^{\mathcal{N }}\) be such that
Since \(B\) is \(A\)-conditionally decisive over \((x,z)\) for \(W\), we have \((x,z) \in P(W(\mathbf{R}^{\prime }))\). Strong Pareto implies that \((y,x) \in P(W(\mathbf{R}^{\prime }))\). By quasi-transitivity, \((y,z) \in P(W(\mathbf{R}^{\prime }))\). The preferences of individuals outside of \(B \cup A\) over \(y\) and \(z\) are not specified, and thus, binary independence implies that \(B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\). Hence, for all \(z \in X \setminus \{ x \},\,B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\).
Take \(z \in X \setminus \{ x \}\). Let \(\mathbf{R}^{\prime \prime } \in \mathcal{R }^{\mathcal{N }}\) be such that
Since \(B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\), we have \((y,z) \in P(W(\mathbf{R}^{\prime \prime }))\). Strong Pareto implies that \((z,x) \in P(W(\mathbf{R}^{\prime \prime }))\). By quasi-transitivity, \((y,x) \in P(W(\mathbf{R}^{\prime \prime }))\). The preferences of individuals outside of \(B \cup A\) over \(x\) and \(y\) are not specified, and thus, binary independence implies that \(B\) is \(A\)-conditionally decisive over \((y,x)\) for \(W\). Hence, for all \(z \in X ,\,B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\). We thus complete the proof of the claim.
By applying the claim again, it follows that if \(B\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\), then \(B\) is \(A\)-conditionally decisive over \((z,w)\) for \(W\). Hence, we have established that \(B\) is \(A\)-conditionally decisive over \((z,w)\) for any choice of distinct alternatives \(z\) and \(w\). \(\square \)
Proof of Theorem 1
Let \(A \subsetneq \mathcal{N }\). We now prove that \(\mathcal D _W(A)\) satisfies the four properties of an ultrafilter.
-
(i)
Let \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) be such that
$$\begin{aligned} \big [ (x,y) \in I(R_i) \text{ for} \text{ all} i \in A \big ] \text{ and} \big [ (x,y) \in P(R_i) \text{ for} \text{ all} i \notin A \big ]. \end{aligned}$$Strong Pareto implies that \((x,y) \in P(W(\mathbf{R}))\). Hence, \(\mathcal{N } \setminus A \in \mathcal D _W(A)\). Similarly, strong Pareto implies that \(\emptyset \notin \mathcal D _W(A)\).
-
(ii)
Suppose that \(B \in \mathcal D _W(A)\) and \(B \subseteq B^{\prime } \subseteq \mathcal{N } \setminus A\). Let \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) be such that
$$\begin{aligned} \big [ (x,y) \in I(R_i) \text{ for} \text{ all} i \in A \big ] \text{ and} \big [ (x,y) \in P(R_i) \text{ for} \text{ all} i \in B^{\prime } \big ]. \end{aligned}$$Since \(B \subseteq B^{\prime }\), we have
$$\begin{aligned} \big [ (x,y) \in I(R_i) \text{ for} \text{ all} i \in A \big ] \text{ and} \big [ (x,y) \in P(R_i) \text{ for} \text{ all} i \in B \big ]. \end{aligned}$$Since \(B \in \mathcal D _W(A)\), it follows that \((x,y) \in P(W(\mathbf{R}))\). Thus, \(B^{\prime } \in \mathcal D _W(A)\).
-
(iii)
Take any three distinct alternatives \(x,y, z \in X\). Suppose that \(B \in \mathcal D _W(A)\) and \(B^{\prime } \in \mathcal D _W(A)\). Let \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) be such that
$$\begin{aligned} \big [ (x,y) \in I(R_i) \text{ and} (y,z) \in I(R_i) \big ]&\text{ for} \text{ all} i \in A ,\\ (x,y) \in P(R_i)&\text{ for} \text{ all} i \in B,\\ (y,z) \in P(R_i)&\text{ for} \text{ all} i \in B^{\prime }. \end{aligned}$$Note that \((x,z) \in P(R_i)\) for all \(i \in B \cap B^{\prime }\). Since \(B,B^{\prime } \in \mathcal D _W(A)\), it follows that \((x,y) \in P(W(\mathbf{R}))\) and \((y,z) \in P(W(\mathbf{R}))\). Quasi-transitivity, which is implied by transitivity, yields
$$\begin{aligned} (x,z) \in P(W(\mathbf{R})). \end{aligned}$$The preferences of individuals outside of \((B \cap B^{\prime }) \cup A\) over \(x\) and \(z\) are not specified, and thus, binary independence implies that \(B \cap B^{\prime }\) is \(A\)-conditionally decisive over \((x,z)\) for \(W\). Hence, \(B \cap B^{\prime } \in \mathcal D _W(A)\).
-
(iv)
Suppose that \(B \subseteq \mathcal{N } \setminus A\) and \(B \notin \mathcal D _W(A)\). Since \(B \notin \mathcal D _W(A)\), there exist \((x,y) \in X \times X\) and \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) such that
$$\begin{aligned} \big [ (x,y) \in I(R_i) \text{ for} \text{ all} i \in A \big ] \text{ and} \big [ (x,y) \in P(R_i) \text{ for} \text{ all} i \in B \big ], \end{aligned}$$but \((x,y) \notin P(W(\mathbf{R}))\). Completeness implies that \((y,x) \in W(\mathbf{R})\). Let \(\mathbf{R}^{\prime } \in \mathcal{R }^{\mathcal{N }}\) be such that
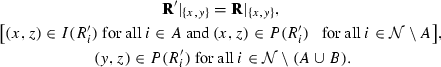
By construction, \((y,z) \in I(R^{\prime }_i) \text{ for} \text{ all} i \in A\). Binary independence implies that \((y,x) \in W(\mathbf{R}^{\prime })\). Since \(\mathcal{N } \setminus A \in \mathcal D _W(A)\), we have \((x,z) \in P(W(\mathbf{R}^{\prime }))\). Transitivity implies that \((y,z) \in P(W(\mathbf{R}^{\prime }))\). Note that
$$\begin{aligned} \big [ (y,z) \in I(R^{\prime }_i) \text{ for} \text{ all} i \in A \big ] \text{ and} \big [ (y,z) \in P(R^{\prime }_i) \text{ for} \text{ all} i \in \mathcal{N } \setminus (A \cup B) \big ]. \end{aligned}$$The preferences of individuals outside of \(\mathcal{N } \setminus B\) over \(y\) and \(z\) are not specified, and thus, binary independence implies that \(\mathcal{N } \setminus (B \cup A)\) is \(A\)-conditionally decisive over \((y,z)\) for \(W\). By Lemma 1, it follows that \(\mathcal{N } \setminus (B \cup A) \in \mathcal D _W(A)\). The proof is complete. \(\square \)
Proof of Theorem 2
In Theorem 1, we do not need rationality requirements to show properties (i) and (ii). Thus, (i) and (ii) can be proved in a similar manner. Moreover, we require only quasi-transitivity to show (iii), and thus, \(\mathcal D _W(A)\) satisfies property (iii). Hence, it suffices to show (iv). Suppose that \(B \subseteq \mathcal{N } \setminus A\) and \(B \notin \mathcal D _W(A)\). Since \(B \notin \mathcal D _W(A)\), there exist \((x,y) \in X \times X\) and \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) such that
but \((x,y) \notin P(W(\mathbf{R}))\). Let \(\mathbf{R}^{\prime } \in \mathcal{R }^{\mathcal{N }}\) be such that

Binary independence implies that \((x,y) \notin P(W(\mathbf{R}^{\prime }))\). Since \(\mathcal{N } \setminus A \in \mathcal D _W(A)\), it follows that \((x,z) \in P(W(\mathbf{R}^{\prime }))\) and \((z,w) \in P(W(\mathbf{R}^{\prime }))\). Semi-transitivity implies that \((y,z) \in P(W(\mathbf{R}^{\prime }))\) or \((x,y) \in P(W(\mathbf{R}^{\prime }))\). Since \((x,y) \notin P(W(\mathbf{R}^{\prime }))\), it follows that \((y,z) \in P(W(\mathbf{R}^{\prime }))\). Binary independence and Lemma 1 together imply that \(\mathcal{N } \setminus B \in \mathcal D _W(A)\). \(\square \)
Proof of Theorem 3
It suffices to show that \(\mathcal D _W(A)\) has property (iv). Suppose that \(B \subseteq \mathcal{N } \setminus A\) and \(B \notin \mathcal D _W(A)\). Since \(B \notin \mathcal D _W(A)\), there exist \((x,y) \in X \times X\) and \(\mathbf{R} \in \mathcal{R }^{\mathcal{N }}\) such that
but \((x,y) \notin P(W(\mathbf{R}))\). Let \(\mathbf{R}^{\prime } \in \mathcal{R }^{\mathcal{N }}\) be such that

Binary independence implies that \((x,y) \notin P(W(\mathbf{R}^{\prime }))\). Since \(\mathcal{N } \setminus A \in \mathcal D _W(A),(x,z) \in P(W(\mathbf{R}^{\prime }))\) and \((w,y) \in P(W(\mathbf{R}^{\prime }))\). The interval-order property implies that \((x,y) \in P(W(\mathbf{R}^{\prime }))\) or \((w,z) \in P(W(\mathbf{R}^{\prime }))\). Since \((x,y) \notin P(W(\mathbf{R}^{\prime }))\), it follows that \((w,z) \in P(W(\mathbf{R}^{\prime }))\). Binary independence and Lemma 1 together imply that \(\mathcal{N } \setminus B \in \mathcal D _W(A)\) \(\square \)
Proof of Theorem 4
It is obvious that properties (i) and(ii) are satisfied. Moreover, we employ only quasi-transitivity to show (iii) in Theorem 1; thus, \(\mathcal D _W(A)\) satisfies property (iii) for all QSDFs. \(\square \)
Proof of Theorem 5
Let \(W\) be an SDF satisfying strong Pareto, and let \(A \subsetneq \mathcal{N }\).
It suffices to show that \(\mathcal D _W(A)\) has property (v). By way of contradiction, suppose that there exist \(K \in \mathbb{N }\) and \(B^0,B^1,\dots ,B^K \in \mathcal D _W(A)\) such that \(\bigcap _{k \in \{0,\dots ,K\}}B^k =\emptyset \). Let \(x^0, x^1,\dots ,x^K\) be distinct alternatives in \(X\). Since \(X\) is an infinite set, we can choose them for any finite number \(K\). Let \(\mathbf{R} \in \mathcal{R }^N\) be such that
We demonstrate that there is such a preference profile \(\mathbf{R}^*\). By the assumption that \(\bigcap _{k \in \{0,\dots ,K\}}B^k =\emptyset \), it follows that for every individual \(i \in \bigcup _{k \in \{0,\dots ,K\}}B^k\), there exists \(k \in \{ 0,\dots , K \}\) such that \(i \notin B^k\). Therefore, each individual’s preferences specified above contain no strict-preference cycle, and thus, there exists the preference profile \(\mathbf{R}^* \in \mathcal{R }^N\). Since \(B^k \in \mathcal D _W(A)\) for all \(k \in \{0,\dots ,K\}\),
This contradicts acyclicity. \(\square \)
Rights and permissions
About this article
Cite this article
Cato, S. Social choice, the strong Pareto principle, and conditional decisiveness. Theory Decis 75, 563–579 (2013). https://doi.org/10.1007/s11238-013-9352-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-013-9352-9