Skip to main content
SpringerLink
Log in

Qualitative difference between solutions of stationary model Boltzmann equations in the linear and nonlinear cases

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

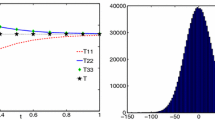
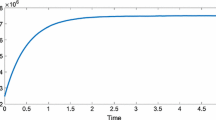
We consider problems for the nonlinear Boltzmann equation in the framework of two models: a new nonlinear model and the Bhatnagar-Gross-Krook model. The corresponding transformations reduce these problems to nonlinear systems of integral equations. In the framework of the new nonlinear model, we prove the existence of a positive bounded solution of the nonlinear system of integral equations and present examples of functions describing the nonlinearity in this model. The obtained form of the Boltzmann equation in the framework of the Bhatnagar-Gross-Krook model allows analyzing the problem and indicates a method for solving it. We show that there is a qualitative difference between the solutions in the linear and nonlinear cases: the temperature is a bounded function in the nonlinear case, while it increases linearly at infinity in the linear approximation. We establish that in the framework of the new nonlinear model, equations describing the distributions of temperature, concentration, and mean-mass velocity are mutually consistent, which cannot be asserted in the case of the Bhatnagar-Gross-Krook model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. Cercignani, Theory and Applications of the Boltzmann Equation, Elsevier, New York (1975).

    Google Scholar 

  2. M. N. Kogan, Dynamics of a Rarefied Gas [in Russian], Nauka, Moscow (1967).

    Google Scholar 

  3. P. L. Bhatnagar, E. P. Gross, and M. Krook, Phys. Rev., 94, 511–525 (1954).

    Article  ADS  MATH  Google Scholar 

  4. N. B. Engibaryan and A. Kh. Khachatryan, Matem. Mod., 16, 67–74 (2004).

    MATH  MathSciNet  Google Scholar 

  5. N. B. Engibaryan and A. Kh. Khachatryan, Comput. Math. Math. Phys., 38, 452–467 (1998).

    MathSciNet  Google Scholar 

  6. A. V. Latyshev and A. A. Yushkanov, Analytic Solution of Boundary Value Problems for Kinetic Theory [in Russian], Moscow Region State Univ., Moscow (2004).

    Google Scholar 

  7. Ts. È. Terdzhyan and A. Kh. Khachatryan, Comput. Math. Math. Phys., 49, 691–697 (2009).

    Article  MathSciNet  Google Scholar 

  8. A. Kh. Khachatryan and S. M. Andriyan, Matem. Mod., 16, 31–42 (2004).

    MATH  MathSciNet  Google Scholar 

  9. M. M. R. Williams, Mathematical Methods in Particle Transport Theory, Butterworth, London (1971).

    Google Scholar 

  10. I. N. Larina and V. A. Rykov, Comput. Math. Math. Phys., 51, 1962–1972 (2011).

    Article  MathSciNet  Google Scholar 

  11. S. K. Loyallka, Phys. Fluids, 14, 2291–2294 (1971).

    Article  ADS  Google Scholar 

  12. L. B. Barichello and C. E. Siewert, European J. Appl. Math., 11, 353–364 (2000).

    Article  MATH  MathSciNet  Google Scholar 

  13. N. B. Yengibaryan and A. Kh. Khachatryan, “On temperature and density jumps in kinetic theory of gases,” in: Horizons in World Physics (A. Reimer, ed.), Vol. 240, Nova Science, New York (2003), pp. 103–117.

    Google Scholar 

  14. L. B. Barichello, A. C. R. Bartz, M. Camargo, and C. E. Siewert, Phys. Fluids, 14, 382–391 (2002).

    Article  ADS  Google Scholar 

  15. S. M. Andriyan and A. Kh. Khachatryan, Comput. Math. Math. Phys., 45, 1982–1989 (2005).

    MathSciNet  Google Scholar 

  16. N. B. Engibaryan and A. Kh. Khachatryan, Theor. Math. Phys., 125, 1589–1592 (2000).

    Article  MATH  MathSciNet  Google Scholar 

  17. A. Kh. Khachatryan and Kh. A. Khachatryan, Theor. Math. Phys., 172, 1315–1320 (2012).

    Article  MATH  MathSciNet  Google Scholar 

  18. C. Villani, Commun. Math. Phys., 234, 455–490 (2003).

    Article  ADS  MATH  MathSciNet  Google Scholar 

  19. A. Kh. Khachatryan and Kh. A. Khachatryan, Mem. Differ. Equ. Math. Phys., 51, 59–72 (2010).

    MATH  MathSciNet  Google Scholar 

  20. L. G. Arabadzhyan and N. B. Engibaryan, J. Soviet Math., 36, 745–791 (1987).

    Article  MATH  Google Scholar 

  21. A. Kh. Khachatryan, “Certain linear and nonlinear problems in physical kinetics [in Russian],” Doctoral dissertation, Byurakan Astrophysical Observatory, Natl. Acad. Sci. Armenia, Byurakan, Aragatsotn Oblast, Armenia (1997).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, Armenian National Academy of Sciences, Yerevan, Armenia

    A. Kh. Khachatryan & Kh. A. Khachatryan

Authors
  1. A. Kh. Khachatryan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kh. A. Khachatryan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Kh. Khachatryan.

Additional information

Dedicated to the memory of Academician V. S. Vladimirov

__________

Translated from Teoreticheskaya i Matematicheskaya Fizika, Vol. 180, No. 2, pp. 272–288, August, 2014.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khachatryan, A.K., Khachatryan, K.A. Qualitative difference between solutions of stationary model Boltzmann equations in the linear and nonlinear cases. Theor Math Phys 180, 990–1004 (2014). https://doi.org/10.1007/s11232-014-0194-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11232-014-0194-6

Keywords

Search

Navigation