Skip to main content
SpringerLink
Log in

Padé approximations for Painlevé I and II transcendents

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

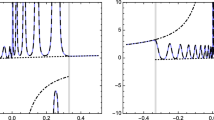
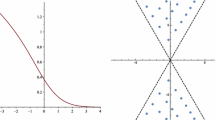
We use a version of the Fair-Luke algorithm to find the Padé approximate solutions of the Painlevé I and II equations. We find the distributions of poles for the well-known Ablowitz-Segur and Hastings-McLeod solutions of the Painlevé II equation. We show that the Boutroux tritronquée solution of the Painleé I equation has poles only in the critical sector of the complex plane. The algorithm allows checking other analytic properties of the Painlevé transcendents, such as the asymptotic behavior at infinity in the complex plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. S. Fokas, A. R. Its, A. A. Kapaev, and V. Yu. Novokshenov, Painlevé Transcendents: The Riemann-Hilbert Approach (Math. Surveys Monogr., Vol. 128), Amer. Math. Soc., Providence, R. I. (2006).

    MATH  Google Scholar 

  2. P. Boutroux, Ann. École Norm., 30, 255–375 (1913); Ann. École Norm., 31, 99–159 (1914).

    MathSciNet  Google Scholar 

  3. A. I. Yablonskii, Vesti A.N. BSSR, Ser. Fiz.-Tekh. Nauk, 3, 30–35 (1959); A. P. Vorob’ev, Differential Equations, 1, 79–81 (1965).

    Google Scholar 

  4. K. Okamoto, Math. Ann., 275, 221–255 (1986).

    Article  MATH  MathSciNet  Google Scholar 

  5. P. A. Clarkson, Phys. Lett. A, 319, 137–144 (2003); J. Math. Phys., 44, 5350–5374 (2003); European J. Appl. Math., 17, 293–322 (2006).

    Article  MATH  ADS  MathSciNet  Google Scholar 

  6. V. G. Marikhin, A. B. Shabat, M. Boiti, and F. Pempinelli, JETP, 90, 553–561 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  7. M. Kh. Chankaev and A. B. Shabat, Theor. Math. Phys., 157, 1514–1524 (2008).

    Article  MATH  MathSciNet  Google Scholar 

  8. J. Nuttall, J. Math. Anal. Appl., 31, 147–153 (1970).

    Article  MathSciNet  Google Scholar 

  9. W. Fair and Y. L. Luke, Math. Comp., 20, 602–606 (1966).

    Article  MATH  MathSciNet  Google Scholar 

  10. A. A. Kapaev, J. Phys. A, 37, 11149–11167 (2004).

    Article  MATH  ADS  MathSciNet  Google Scholar 

  11. P. G. Grinevich and S. P. Novikov, St. Petersburg Math. J., 6, 553–574 (1995).

    MathSciNet  Google Scholar 

  12. B. Dubrovin, T. Grava, and C. Klein, Nonlinear Sci., 19, 67–94 (2009); arXiv:0704.0501v3 [math.AP] (2007).

    MathSciNet  Google Scholar 

  13. A. A. Kapaev, Differential Equations, 24, 1107–1115 (1988).

    MATH  MathSciNet  Google Scholar 

  14. N. Joshi and A. V. Kitaev, Stud. Appl. Math., 107, 253–291 (2001).

    Article  MATH  MathSciNet  Google Scholar 

  15. C. Tracy and H. Widom, Comm. Math. Phys., 177, 727–754 (1996).

    Article  MATH  ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, Ufa Science Center, RAS, Ufa, Russia

    V. Yu. Novokshenov

Authors
  1. V. Yu. Novokshenov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. Yu. Novokshenov.

Additional information

Prepared from an English manuscript submitted by the author; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, Vol. 159, No. 3, pp. 515–526, June, 2009.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Novokshenov, V.Y. Padé approximations for Painlevé I and II transcendents. Theor Math Phys 159, 853–862 (2009). https://doi.org/10.1007/s11232-009-0073-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11232-009-0073-8

Keywords

Search

Navigation