Abstract
In this paper, I develop an original view of the structure of space—called infinitesimal atomism—as a reply to Zeno’s paradox of measure. According to this view, space is composed of ultimate parts with infinitesimal size, where infinitesimals are understood within the framework of Robinson’s (Non-standard analysis. North-Holland, Amsterdam, 1966) nonstandard analysis. Notably, this view satisfies a version of additivity: for every region that has a size, its size is the sum of the sizes of its disjoint parts. In particular, the size of a finite region is the sum of the sizes of its infinitesimal parts. Although this view is a coherent approach to Zeno’s paradox and is preferable to Skyrms’s (Physics, philosophy and psychoanalysis. Volume 76 of the series Boston studies in the philosophy of science, pp 223–254, 1983) infinitesimal approach, it faces both the main problem for the standard view (the problem of unmeasurable regions) and the main problem for finite atomism (Weyl’s tile argument), leaving it with no clear advantage over these familiar alternatives.



Similar content being viewed by others
Notes
Infinitesimals first appeared in Democritus’s work (450 B.C.E) only to be banished by Eudoxus (350 B.C.E). They reappeared during the invention of modern calculus, but were attacked and eventually abandoned in mainstream nineteenth-century mathematics (Bell 2017).
I explore other technical approaches to infinitesimals such as smooth infinitesimal analysis elsewhere.
In standard analysis, even though we typically only sum up countably many numbers, summing up zeros is a notable exception. The following general definition of a sum over non-negative numbers indexed by an arbitrary set implies that zeros always sum up to zero. Let HUGE be an indexing set for some non-negative numbers. Let PAR be the set of partial sums of numbers indexed by finite subsets of HUGE. We define the sum of the numbers indexed by HUGE to be the least upper bound of PAR. It follows from this definition that zeros, even if uncountably many, sum up to zero. This definition, when applies to a countable set of positive numbers, coincides with the more familiar notion of sum in standard analysis defined as the limit of partial sums of an infinite sequence.
There is also a more elementary analogous result in the one-dimensional case, which involves the construction of “Vitali sets” (see Skyrms 1983, pp. 238–239).
The half-open intervals, while they make a helpful intuitive picture, should not be taken too literally. I am using certain mathematical objects to represent parts of space, but not every mathematical feature corresponds to a genuine spatial feature. In particular, the asymmetric half-openness does not correspond to any real feature of the minims that the intervals represent. Rather, the representation in question is a one-to-one correspondence between the half-open intervals and the minims that preserves length, order, and connectedness. Note that in the case of atomistic space, I take “connectedness” (or “adjacency”) to be primitive (see Forrest 1995; Roeper 1997). Intuitively, two regions are connected if there is no gap between them.
This can be derived from the theorem that every infinite hyperfinite set is uncountable (Goldblatt 1998, p. 141). In every monad, there are more than hyperfinitely many minims.
For those who are mathematically informed, the measure is closely related to Loeb measure in NSA. The main difference is that Loeb measure is real-valued and is defined over a \(\sigma \)-algebra which includes the domain of the hyperreal measure as a proper subset.
There is a related worry of arbitrariness that I do not discuss in this paper. The worry is that it is arbitrary that a minim has a length of a particular infinitesimal. As pointed out by the anonymous referee, Reeder (2015) discussed this worry and suggested that we should represent a minim by a monad instead. I prefer the approach in this paper because it allows for a richer measure theory with attractive features. We can add up the lengths of minims to obtain an infinitesimal or a finite length, and the measure of any measurable region is the sum of its ultimate parts. In contrast, monads are unmeasurable, and we cannot add up their lengths. In fact, the measure theory of Reeder’s approach would be less rich than the standard measure: they are otherwise the same except that points of length zero are replaced by unmeasurable monads.
Note that this is a distinct feature of infinitesimal atomism that is not present in, for example, Skryms’s (1983) suggestion. The measure theory Skyrms suggested is only finitely additive (pp. 241–242).
This is because the union of hyperfinitely many disjoint hyperfinite sets is still hyperfinite, just like the union of finitely many disjoint finite sets is still finite.
In contrast, Skyrms’s (1983) approach violates Weak Additivity. The fact that Skyrms’s suggested measure is only finitely additive (see Footnote 11) means that for any region of a finite size, its measure is not the sum of the measures of its composing points, since every finite region contains uncountably many points. This feature, I think, makes his approach less attractive than mine. The violation of the intuitive principle of Weak Additivity alone is a cost. Moreover, this violation also undermines the motivation for Regularity. If the measure of an extended region is not determined by the measures of its ultimate parts, does it matter whether the ultimate parts have measure zero? It doesn’t seem so bad to have an unextended point per se. What’s bad rather seems to be the failure of Additivity when those unextended points compose an extended region. So, it is not clear that Skyrms’s approach is an improvement over the standard view.
This version of additivity is as strong as it can get without building in Unrestricted Composition, the principle that any regions have a fusion. Under Unrestricted Composition, Strong Additivity entails the full-blown version of additivity: for arbitrarily many measurable disjoint regions, they have a fusion, their fusion is measurable, and the measure of their fusion is the sum of the measures of those regions.
Here I assume that the fusion of regions is also a region. This follows from my stipulation that “region” simply means a part of the continuum, together with the standard mereological principle that the fusion of parts of X is still a part of X.
More precisely, the sequence of distances you walked is \(\langle 1/2^n\rangle \), where n ranges over all natural numbers.
Like a monad, the sets of the minims in question are not internal sets, sets that are characterizable in the language of standard analysis.
Every region composed of countably infinitely many minims is unmeasurable, and every monad contains uncountably many countably infinite collections of minims.
The ultrafilter construction of the hyperreal system requires only the Boolean prime ideal theorem, which is strictly weaker than the axiom of choice. Thanks to an anonymous referee for pointing out this difference.
To adopt this principle, we must impose a further constraint on the set of minims M: it must be bounded by hyperreal numbers. Otherwise the minims in M would not be hyperfinitely many, and thus would not compose a region.
Here, we assume that M is bounded by hyperreal numbers (Footnote 20). Also see Goldblatt (1998, pp. 166–73) for more information about internal sets.
Fus\(_\phi z\) can be defined in terms of parthood in a first-order language (let “Pxy” mean x is a part of y): Fus\(_\phi z\) iff \(\forall x(\phi x\rightarrow Pxz)\wedge \forall y(\forall x(\phi x\rightarrow Pxy)\rightarrow Pzy)\). (Cotnoir and Varzi 2018)
Recall that infinitesimals are those whose absolute values are smaller than any positive real number. But in NSA, the set of positive hyperreal numbers satisfies the exact same first-order truths as the set of positive real numbers in the language of standard analysis. So the set of positive real numbers is not expressible, which means that the set of infinitesimals is not expressible either.
My presentation of the argument draws on Salmon (1980).
Although it is possible to distinguish between “length,” a measure defined over regions of space, and “distance,” a metric defined over pairs of points or atoms, it is standardly assumed that the argument can be put in terms of distances.
In standard differential geometry, a path between two points is a continuous function from the real interval [0,1] to the space, which takes 0 to one of the two points and 1 to the other one.
Connectedness is a primitive topological notion for finite atomism and infinitesimal atomism.
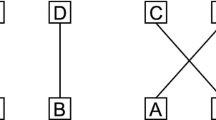
Another intuitive option is to stipulate that two tiles are connected iff they are horizontally or vertically adjacent. Under this option, the diagonal BC is the zigzag region shown below. This option is similarly problematic.

Skyrms’s continuum might be able to escape this argument. Although Skryms did not explicitly define a distance function over the continuum, he can resort to the standard distance function over standard space because Skyrms’s continuum is isomorphic to standard space. The infinitesimal measure of a “point” does not play any role in determining distances.
References
Arntzenius, F. (2008). Gunk, topology and measure. Oxford studies in metaphysics: Volume 4 Oxford: OUP.
Arntzenius, F. (2003). Is quantum mechanics pointless. Philosophy of Science, 70(5), 1447–1457.
Bell, J. L. (2017). Continuity and infinitesimals. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/sum2017/entries/continuity/.
Bricker, P. (1993). The fabric of space: Intrinsic vs. extrinsic distance relations. Midwest Studies in Philosophy, 18(1), 271–294.
Bricker, P. (2015). Composition as a kind of identity. Inquiry, 59(2), 264–294.
Chen, L. (Manuscript a) Infinitesimal gunk. Manuscript submitted for publication.
Chen, L. (Manuscript b) Intrinsic local distances: A mixed solution to Weyl’s tile argument. Manuscript submitted for publication.
Conway, J. H. (1976). On number and games. London Mathematical Society Monographs. London: Academic Press.
Cotnoir, A. J., & Varzi, A. C. (2018). Natural axioms for classical mereology. The Review of Symbolic Logic, 12(1), 201–208.
Forrest, P. (1995). Is space–time discrete or continuous?—An empirical question. Synthese, 103, 327–354.
Forrest, P. (2004). Grit or gunk: Implications of the Banach–Tarski paradox. The Monist, 87(3), 351–370.
Furley, D. J. (1967). “Indivisible magnitude,” two studies in the Greek atomists. Princeton: Princeton University Press.
Geroch, R. (1972). Einstein algebra. Communications in Mathematical Physics, 26(4), 271–275.
Goldblatt, R. (1998). Lectures on the hyperreals: An introduction to non-standard analysis. New York: Springer.
Grünbaum, A. (1973). Philosophical problems of space and time (Vol. XII). Boston studies in the philosophy of science Dordrecht: D. Reidel Publishing Co.
Hogan, C. (2012). Interferometers as probes of Planckian quantum geometry. Physics Review D, 85(6), 064007.
Lawvere, F. W. (1980). Toward the description in a smooth topos of the dynamically possible motions and deformations of a continuous body. Cahiers de Topologie et Géométrie Différentielle Catégoriques, 21(4), 277–392.
Lewis, D. (1991). Parts of classes. Oxford: Blackwell.
Maudlin, T. (2014). New foundation for physical geometry: The theory of linear structures. Oxford: Oxford University Press.
Reeder, P. (2015). Zeno’s arrow and the infinitesimal calculus. Synthese, 192, 1315–1335.
Robinson, A. (1966). Non-standard analysis. Amsterdam: North-Holland.
Roeper, P. (1997). Region-based topology. Journal of Philosophical Logic, 26(3), 251–309.
Russell, B. (1958). A critical exposition of the philosophy of Leibniz (2nd ed.). London: Allen & Unwin.
Russell, J. (2008). The structure of gunk: Adventures in the ontology of space (Vol. 4). Oxford studies in metaphysics Oxford: OUP.
Salmon, W. (1980). Space, time, and motion. Minneapolis: University of Minnesota Press.
Skyrms, B. (1983) Zeno’s paradox of measure. In Physics, philosophy and psychoanalysis. (Volume 76 of the series Boston studies in the philosophy of science) (pp. 223–254).
Solovay, R. M. (1970). A model of set-theory in which every set of reals is Lebesgue measurable. Annals of Mathematics, Second Series, 92, 1–56.
Van Bendegem, J. P. (1987). Zeno’s paradoxes and the Weyl tile argument. Philosophy of Science, 54(2), 295–302.
Van Bendegem, J. P. (1997). In defence of discrete space and time. Logique et Analyse, 38(150–152), 127–150.
Wagon, S. (1985). The Banach–Tarski paradox (encyclopedia of mathematics and its applications). Cambridge: Cambridge University Press.
Weyl, H. (1949). Philosophy of mathematics and natural sciences. Princeton: Princeton University Press.
Zimmerman, Dean. (1996). Indivisible parts and extended objects: Some philosophical episodes from topology’s prehistory. The Monist, 79(1), 148–180.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Special thanks to Jeffrey Russell and Phillip Bricker for their extensive feedback on early drafts of the paper. Many thanks to the referees of Synthese for their very helpful comments. I’d also like to thank the participants of Umass dissertation seminar for their useful feedback on my first draft.
Rights and permissions
About this article
Cite this article
Chen, L. Do simple infinitesimal parts solve Zeno’s paradox of measure?. Synthese 198, 4441–4456 (2021). https://doi.org/10.1007/s11229-019-02350-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-019-02350-2