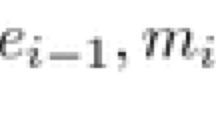Abstract
A measure of coherence is said to be truth conducive if and only if a higher degree of coherence (as measured) results in a higher likelihood of truth. Recent impossibility results strongly indicate that there are no (non-trivial) probabilistic coherence measures that are truth conducive. Indeed, this holds even if truth conduciveness is understood in a weak ceteris paribus sense (Bovens & Hartmann, 2003, Bayesian epistemology. New York, Oxford: Oxford University Press; Olsson, 2005, Against coherence: Truth probability and justification. Oxford: Oxford University Press). This raises the problem of how coherence could nonetheless be an epistemically important property. Our proposal is that coherence may be linked in a certain way to reliability. We define a measure of coherence to be reliability conducive if and only if a higher degree of coherence (as measured) results in a higher probability that the information sources are reliable. Restricting ourselves to the most basic case, we investigate which coherence measures in the literature are reliability conducive. It turns out that, while a number of measures fail to be reliability conducive, except possibly in a trivial and uninteresting sense, Shogenji’s measure and several measures generated by Douven and Meijs’s recipe are notable exceptions to this rule.
Similar content being viewed by others
References
Audi R. (2002). The sources of knowledge. In: Moser P.K. (Ed), The oxford handbook of epistemology. (pp. 71–94). Oxford University Press.
BonJour L. (2000). The structure of empirical knowledge. Cambridge Massachusetts, Harvard University Press
Bovens L., Fitelson B., Hartmann S., Snyder J. (2002). Too odd (not) to be true: A reply to Erik J. Olsson. British Journal for the Philosophy of Science, 53, 539–563
Bovens L., Hartmann S. (2003). Bayesian epistemology. New York Oxford, Oxford University Press
Bovens L., Olsson E.J. (2000). Coherentism, reliability and Bayesian networks. Mind, 109, 686–719
Carnap R. (1962). Logical foundations of probability (2nd ed). Chicago, University of Chicago Press
Christensen D. (1999). Measuring confirmation. The Journal of Philosophy, 96, 437–461
Cohen L.J. (1977). The probable and the provable. Oxford, Oxford University Press
Davidson D. (1986). A coherence theory of knowledge and truth. In: LePore E. (Ed), Truth and Interpretation. Oxford, Blackwell, pp. 307–319
Douvens I., Meijs W. (2005). Measuring coherence. Synthese (to be published).
Dietrich F., Moretti L. (2005). On coherent sets and the transmission of confirmation. Philosophy of Science, 72(3): 403–424
Ewing A.C. (1934). Idealism: A critical survey. London, Methuen
Finch H.A. (1960). Confirming power of observations metricized for decisions among hypotheses. Philosophy of Science, 27, 293–307
Fitelson B. (2001). Studies in Bayesian confirmation theory. Ph.D thesis, University of Wisconsin at Madison. Online: http://fitelson.org/thesis.pdf
Fitelson B. (2003). A probabilistic theory of coherence. Analysis, 63, 194–199
Fitelson B. (2004). Two technical corrections to my coherence measure. http://fitelson.org/ coherence2.odf
Gillies D. (1986). In defense of the Popper-Miller argument. Philosophy of Science, 53, 110–113
Glass D.H. (2002). Coherence, explanation, and Bayesian networks. In Proceedings of the Irish conference on AI and cognitive science, Lecture notes in AI, Vol. 2646, pp. 256–259 New York: Springer-Verlag.
Good I.J. (1984). The best explicatum for weight of evidence. Journal of Statistical Computation and Simulation, 19, 294–299
Horwich P. (1998). Wittgensteinian Bayesianism. In: Curd M., Cover J.A. (Eds), Philosophy of science: The central issues. New York and London, Norton, pp. 607–624
Jeffrey R. (1987). Alias Smith and Jones: The testimony of the senses. Erkenntnis, 26, 391–399
Jeffrey R. (1992). Probability and the art of judgment. Cambridge, Cambridge University Press
Lehrer K. (1990). Theory of knowledge. Boulder Colo, Westview Press
Levi I. (1962). Corroboration and rules of acceptance. Brititsh Journal for the Philosophy of Science, 13, 307–313
Lewis C.I. (1946). An analysis of knowledge and valuation. LaSalle, Ill.: Open Court.
Milne P. (1996). log[p(h/eb)/p(h/b)] is the one true measure of confirmation. Philosophy of Science, 63, 21–26
Nozick R. (1981). Philosophical explanations. Cambridge Massachusetts, Harvard University Press
Olsson E.J. (2002a). What is the problem of coherence and truth?. The Journal of Philosophy, 99, 246–272
Olsson E.J. (2002b). Corroborating testimony, probability and surprise. British Journal for the Philosophy of Science, 53, 273–288
Olsson E.J. (2002c). Corroborating testimony and ignorance: A reply to Bovens, Fitelson, Hartmann and Snyder. British Journal for the Philosophy of Science, 53, 565–572
Olsson E.J. (2005). Against coherence: Truth, probability and justification. Oxford, Oxford University Press
Olsson E.J. (to appear). The impossibility of coherence. Erkenntnis.
Popper K. (1954). Degree of confirmation. British Journal for the Philosophy of Science, 5, 143–149
Rescher N. (1958). Theory of evidence. Philosophy of Science, 25, 83–94
Rescher N. (1973). The coherence theory of truth. Oxford, Oxford University Press
Rosenkrantz R. (1994). Bayesian confirmation: Paradise regained. The British Journal for the Philosophy of Science, 45, 467–476
Russell B. (1912). The problems of philosophy. London, Oxford University Press
Schlesinger G. (1995). Measuring degrees of confirmation. Analysis, 55, 208–212
Shogenji T. (1999). Is coherence truth conducive?. Analysis, 59, 338–345
Siebel M. Equivalent testimonies as a touchstone of coherence measures. Unpublished manuscript.
Thagard P. (2000). Coherence in thought and action. Cambridge Mass, MIT Press
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Olsson, E.J., Schubert, S. Reliability conducive measures of coherence. Synthese 157, 297–308 (2007). https://doi.org/10.1007/s11229-006-9056-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-006-9056-6