Abstract
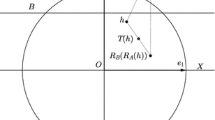
We expand upon previous work that examined the behavior of the iterated Douglas-Rachford method for a line and a circle by considering two generalizations:that of a line and an ellipse and that of a line together with a p-sphere. With computer assistance we discover a beautiful geometry that illustrates phenomena which may affect the behavior of the iterates by slowing or inhibiting convergence for feasible cases. We prove local convergence near feasible points, and—seeking a better understanding of the behavior—we employ parallelization in order to study behavior graphically. Motivated by the computer-assisted discoveries, we prove a result about behavior of the method in infeasible cases.
Similar content being viewed by others
References
Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Recent results on Douglas-Rachford methods for combinatorial optimization problems. J. Optim. Theory Appl. 163, 1–30 (2014)
Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Douglas-Rachford feasibility methods for matrix completion problems. ANZIAM J. 55(4), 299–326 (2014)
Aragón Artacho, F.J., Borwein, J.M.: Global convergence of a non-convex Douglas-Rachford iteration. J. Glob. Optim. 57(3), 753–769 (2013)
Bailey, D.H., Borwein, J.M.: Experimental computation as an ontological game changer: the impact of modern mathematical computation tools on the ontology of mathematics. In: Mathematics, Substance and Surmise: Views on the Meaning and Ontology of Mathematics, pp. 25–67. Springer, Berlin
Bauschke, H.H., Bello Cruz, J.Y., Nghia, T.T.A., Phan, H.M., Wang, X.: The rate of linear convergence of the Douglas-Rachford algorithm for subspaces is the cosine of the Friedrichs angle. J. Approx. Theory 185, 63–79 (2014)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, Berlin (2011)
Bauschke, H.H., Combettes, P.L., Luke, D.R.: Phase retrieval, error reduction algorithm, and Fienup variants: a view from convex optimization. J. Opt. Soc. Am. 19, 1334–1345 (2002)
Bauschke, H.H., Moursi, W.M.: On the Douglas-Rachford algorithm. Math. Program. 164, 263–284 (2017)
Borwein, J.M., Sims, B.: The Douglas-Rachford algorithm in the absence of convexity. In: Fixed-Point Algorithms for Inverse Problems in Science and Engineering, Springer Optimization and its Applications, vol. 49, pp. 93–109 (2011)
Borwein, J.M., Tam, M.K.: Reflection methods for inverse problems with applications to protein conformation determination. In: Springer Volume on the CIMPA school Generalized Nash Equilibrium Problems, Bilevel Programming and MPEC, New Delhi (2012)
Benoist, J.: The Douglas-Rachford algorithm for the case of the sphere and the line. J. Glob. Optim. 63, 363–380 (2015)
Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, Berlin (2011)
Deutsch, F.: Rate of convergence of the method of alternating projections. In: Brosowski, B., Deutsch, F. (eds.) Parametric Optimization and Approximation, pp. 96–107. Birkhäuser, Basel (1983)
Dontchev, A.L.: Private communication
Douglas, J., Rachford, H.H.: On the numerical solution of the heat conduction problem in 2 and 3 space variables. Trans. AMS 82, 421–439 (1956)
Lakshmikantham, V., Trigiante, D.: Theory Of Difference Equations - Numerical Methods And Applications. Marcel Dekker, New York (2002)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)
Borwein, J.M., Lindstrom, S.B., Sims, B., Schneider, A., Skerritt, M.P.: Appendix to dynamics of the Douglas-Rachford method for ellipses and p-spheres. Available at: http://hdl.handle.net/1959.13/1330341 (2017)
Acknowledgments
The authors wish to especially thank one of the referees for their careful reading of the manuscript and their several suggestions which have significantly improved the readability of the final version.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is dedicated to the memory of Jonathan M. Borwein our greatly missed friend, mentor, and colleague. His early contributions to this paper, like his contributions to so much else, were both vital and inspirational.
Rights and permissions
About this article
Cite this article
Borwein, J.M., Lindstrom, S.B., Sims, B. et al. Dynamics of the Douglas-Rachford Method for Ellipses and p-Spheres. Set-Valued Var. Anal 26, 385–403 (2018). https://doi.org/10.1007/s11228-017-0457-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11228-017-0457-0