Abstract
An erotetic calculus for a given logic constitutes a sequent-style proof-theoretical formalization of the logic grounded in Inferential Erotetic Logic (\({\mathsf{IEL}}\)). In this paper, a new erotetic calculus for Classical Propositional Logic (\({\mathsf{CPL}}\)), dual with respect to the existing ones, is given. We modify the calculus to obtain complete proof systems for the propositional part of paraconsistent logic \({\mathsf{CLuN}}\) and its extensions \({\mathsf{CLuNs}}\) and \({\mathsf{mbC}}\). The method is based on dual resolution. Moreover, the resolution rule is non-clausal. According to the authors knowledge, this is the first account of resolution for \({\mathsf{mbC}}\). Last but not least, as the method is grounded in \({\mathsf{IEL}}\), it constitutes an important tool for the so-called question-processing.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Avron, A., The method of hypersequents in the proof theory of propositional non-classical logics, in W. Hodges, M. Hyland, C. Steinhorn, and J. Truss, (eds.), Logic: Foundations to Applications, Oxford Science Publications, New York, 1996, pp. 1–32.
Batens D.: Paraconsistent extensional propositional logics. Logique et Analyse 90–91, 195–234 (1980)
Batens, D., Inconsistency-adaptive logics, in E. Orłowska, (ed.), Logic at Work. Essays Dedicated to the Memory of Helena Rasiowa, Springer Verlag, Heidelberg, 1998, pp. 445–472.
Batens, D., and K. De Clercq, A rich paraconsistent extension of full positive logic, Logique et Analyse 185–188:227–257, 2005.
Batens, D., K. De Clercq, and N. Kurtonina, Embedding and interpolation for some paralogics. The propositional case, Reports on Mathematical Logic 33:29–44, 1999.
Batens, D., and J. Meheus, A tableau method for inconsistency-adaptive logics, in R. Dyckhoff, (ed.), Automated Reasoning with Analytic Tableaux and Related Methods, Springer, Dordrecht, 2000, pp. 127–142.
Carnielli, W. A., and M. E. Coniglio, Logics of formal inconsistency, in F. Guenthner and Dov M. Gabbay, (eds.), Handbook of Philosophical Logic, vol. 14, Springer, Dordrecht, 2013, pp. 1–93.
Carnielli, W. A., and J. Marcos, A taxonomy of \({\mathbf{C}}\)-systems, in I. M. L. D’Ottaviano, W. A. Carnielli, and M. E. Coniglio, (eds.), Paraconsistency—The Logical Way to the Inconsistent, Marcel Dekker, New York, 2000, pp. 1–94.
Coniglio, M. E., and T. G. Rodrigues, Some investigations on \({\mathsf{mbC}}\) and \({\mathsf{mCi}}\), in C. A. Mortari, (ed.), Tópicos de lógicas não clássicas, NEL/UFSC, Florianópolis, 2014, pp. 11–70.
Fitting M.: First-Order Logic and Automated Theorem Proving. Springer Verlag, Berlin (1990)
Indrzejczak, A., Natural Deduction, Hybrid Systems and Modal Logics, vol. 30 of Trends in Logic, Springer, Dordrecht, 2010.
Indrzejczak, A., A survey of nonstandard sequent calculi, Studia Logica 102(6):1295–1322, 2014.
Leszczyńska, D., Socratic proofs for some normal modal propositional logics, Logique et Analyse 47(185–188):259–285, 2004.
Leszczyńska-Jasion D.: The Method of Socratic Proofs for Normal Modal Propositional Logics. Adam Mickiewicz University Press, Poznań (2007)
Leszczyńska-Jasion, D., The method of Socratic proofs for modal propositional logics: K5, S4.2, S4.3, S4M, S4F, S4R and G, Studia Logica 89(3):371–405, 2008.
Leszczyńska-Jasion, D., M. Urbański, and A. Wiśniewski, Socratic trees, Studia Logica 101(5):959–986, 2013.
Ligeza, A., Logical Foundations for Rule-Based Systems, vol. 11 of Studies in Computational Intelligence, Springer, Heidelberg, 2006.
Negri S., von Plato J.: Structural Proof Theory. Cambridge University Press, Cambridge (2001)
Neto, A. G. S. S., and M. Finger, Effective prover for minimal inconsistency logic, in M. Bramer, (ed.), IFIP International Federation for Information Processing, Springer, New York, 2006, pp. 465–474.
Robinson J. A.: A machine oriented logic based on the resolution principle. Journal of the ACM 12, 23–41 (1965)
Skura T. F.: Intuitionistic Socratic procedures. Journal of Applied Non-Classical Logics 15(4), 453–464 (2005)
Skura, T. F., Refutation systems in propositional logic, in F. Guenthner and D. M. Gabbay, (eds.), Handbook of Philosophical Logic, vol. 16, Springer, New York, 2011, pp. 115–157.
Smullyan R. M.: First-Order Logic. Springer-Verlag, Berlin (1968)
Troelstra, A. S., and H. Schwichtenberg, Basic Proof Theory, 2nd edn., Camridge University Press, Cambridge, 2000.
Wiśniewski A.: The Posing of Questions: Logical Foundations of Erotetic Inferences. Kluwer Academic Publishers, Dordrecht (1995)
Wiśniewski, A., Socratic proofs, Journal of Philosophical Logic 33(3):299–326, 2004.
Wiśniewski, A., Questions, Inferences and Scenarios, vol. 46 of Studies in Logic. Logic and Cognitive Systems, College Publications, London, 2013.
Wiśniewski A., Shangin V.: Socratic proofs for quantifiers. Journal of Philosophical Logic 35(2), 147–178 (2006)
Wiśniewski, A., and V. Shangin,
 (Some admissible rules in the system of Socratic proofs),
(Some admissible rules in the system of Socratic proofs),  7(5):77–88, 2007.
7(5):77–88, 2007.Wiśniewski A., Vanackere G., Leszczyńska D.: Socratic proofs and paraconsistency: A case study. Studia Logica 80(2–3), 433–468 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chlebowski, S., Leszczyńska-Jasion, D. Dual Erotetic Calculi and the Minimal \({\mathsf{LFI}}\) . Stud Logica 103, 1245–1278 (2015). https://doi.org/10.1007/s11225-015-9617-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11225-015-9617-0


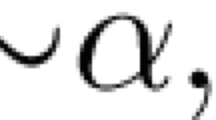

 (Some admissible rules in the system of Socratic proofs),
(Some admissible rules in the system of Socratic proofs),  7(5):77–88, 2007.
7(5):77–88, 2007.