Introduction

Zwitterions are compounds with oppositely charged centers and often referred to as betaines dipolar ions, salt-bridged containing molecules and inner salts. These species are exeptionally important in biological transformations, organic sythesis and preparation of novel materials of various applications in medicine, pharmacy and industry [1–3]. Zwitterions contain a quaternary nitrogen atom and a carboxylate group, separated by one or more carbon atoms. The ammonium group is inert as a hydrogen bond center, whereas the carboxylate group is basic [4, 5]. At normal conditions betaines crystallize as hydrates, because of the strong H-acceptor carboxylic group and no acidic H-donors. The formation of hydrates is technologically important, however it generally cannot be always predicted [6–11]. The zwitterionic hydrates crystallize with one, two, three or more water molecules [11]. Being good proton-acceptors, dipolar ions form 1:1, 2:1 and 3:2 adducts with inorganic acids, which crystallize as anhydrous compounds or hydrates. In the 2:1 complex two zwitterions are bridged by the H-atom, forming a homoconjugated cation with an inorganic anion as a counter ion. Most of the 2:1 complexes are anhydrous and only few of them crystallize as hydrates. The water molecule interacts with the anion [12–17]. In the 1:1:H2O complexes of zwitterions with inorganic acids, the carboxylate group is protonated and it forms H-bonds COOH···OH2 to water molecules, which are further H-bonded to halogen anions [11, 18–24]. However, in the complex of betaine hydrogen selenate monohydrate the anion interacts both with the carboxylate group of the protonated betaine and water [25]. Moreover, there are some exceptions from the typical interactions described above. In 3-hydroxypyridine betaine hydrochloride monohydrate the hydroxy substituent interacts with the water molecule, while the carboxylic group with the chloride anion, through the OH···OH2 and COOH···Cl– hydrogen bonds of 2.566(2) and 2.993(2) Å, respectively [26]. In 4-amino-1-(2-carboxyethyl)-pyridinium bromide hemihydrate two symmetry independent carbonyl groups are H-bonded, one forming a centrosymmetric dimer and the second symmetry-independent group is H-bonded to the water molecule. Hence the complex is built of Br– - H2O - cation - Br– cation - cation - Br– - cation - H2O - Br– chain links [27]. The unusual water-betaine interactions are observed in 1-methylquinolinium-3-carboxylic chloride monohydrate, where the unit cell comprises six symmetry-independent complexes. In four of them the 1-methylquinolinium-3-carboxylic groups are H-bonded to water molecules, while in two others the carboxylate groups are H-bonded to hydronium ions [28]. The complexes of betaines with acids display interesting physical properties, including phase transitions, ferroelectric, antiferroelectic and ferroelastic behavior, as well as commensurate and incommensurate phases [29–41].

An interesting group of zwitterionic compounds are benzbetaines, ortho-, meta- and para-trimethylammonium benzoates, and their esters, hydrates and salts with halogen anions [17, 42–51]. Quaternization of dimethylaminobenzoic acids by an excess methyl iodide in methanol depends on temperature and time of reaction [42]. In some condition the methyl group can transfer from the amino group to the carboxylic group to give an ester derivative [42, 51].

Recently, we reported two exceptionally similar polymorphs of a unique anhydrous [di-(3-trimethylammonium-benzoic acid)-(3-trimethylammonium-benzoate)]diiodide 3:2 complex [52]. Presently, we have obtained a highly pseudosymmetric hydrate of 3-trimethylammonium-benzoic acid iodide (1) 1:1 complex, shown in Fig. 1, and we studied its structure by single-crystal X-ray diffraction in the temperature range of 130-296 K, by differential scanning calorimetry (DSC), thermogravimetry (TG), differential thermal analysis (DTA), FTIR spectroscopy and DFT calculations.

Fig. 1.
figure 1

The symmetry independent unit of 3-(trimethylammonium)-benzoic acid iodide hydrate. Thermal ellipsoids have been drawn at the 50% probability level. Independent cations A (atoms C1-C10), B (C11-C20), C (C21-C30) and D (C31-C40) are highlighted red, green, blue, and gray, respectively (all atomic labels, of four independent molecules and including H-atoms, are shown in Fig. S1, in Supplementary Material).

Full size image

Experimental section

Synthesis

To a solution of 6 g (0.0365 mol) of 3-dimethylamino-benzoic acid in 30 ml CH3OH, 5.7 g (0.040 mol) of methyl iodide was added and stirred at 25 °C for 28 h. The crude product was filtered off, washed with acetonitrile. Yellow crystals were recrystallized from water, m.p. 189-194 °C. Analysis for C10H14NO2·H2O, m.wt. 327.15. Calc.: %C 36.94, %H 4.96, %N 4.31; Found: %C 37.09, %H 4.86, %N 4.28.

Measurements

The crystals of 3-(trimethylammonium)-benzoic acid iodide hydrate, 1, were obtained in the form of long plates, however their single-crystal quality was low. X-Ray diffraction data were measured using an Oxford Diffraction Excalibur EOS-CCD diffractometer, equipped with an EOS-CCD detector, with MoKα radiation, and a Cryosystem low-temperature attachment. Single-crystal diffraction data were collected at the 130-296 K temperature range. The structure was solved by direct methods with program SHELXS and refined on F 2 by full-matrix least-squares with SHELXL [53]. The positions of H-atoms in the cations were located from the molecular geometry and those in the water molecules were found from the difference Fourier maps and then the O-H distances were constrained in the refinement. The anisotropic thermal parameters were refined for the non-H-atoms, some of them with constrains reducing their elongation, and isotropic U iso parameters for H atoms were linked to U eq of their carriers. The atomic labels of non-H atoms in independent cations B/C/D are differentiated by adding 10/20/30 to the atom numbers of cation A, respectively; the O-atoms of water molecules are independently numbered as O1w, O2w, O3w and O4w, where letter ‘w’ indicates the water molecule; the labels of H-atoms are made of letter ‘H’ and the number of the label of their carriers, and additionally numbered by letters ‘a’, ‘b’ and ‘c’ if required, while H-atoms in water molecules are numbered by additional digits 1 and 2: all labels are shown explicitly in Fig. S1 in Supplementary Material. The crystal data, together with the details concerning data collection and structure refinement are given in Tables 1 and S1 (in the Supplementary Material). The crystal data have been deposited in the Cambridge Crystallographic Database Centre as Supplementary publications CCDC 1443312-1443323. Molecular illustrations were prepared using program Mercury CSD 3.3 [54].

Table 1. Selected crystal data of 3-(trimethylammonium)-benzoic acid iodide hydrate at 296 K (cf. Table S1 in the Supplementary Material)
Full size table

FTIR spectrum of 1 was measured in the KBr disk using a Bruker IFS 66v/S instrument, with the resolution of 2 cm-1. The spectra were accumulated of 64 scans.

The differential scanning calorimetry (DSC) of 1 was performed with a DSC THASS XP-10 calorimeter. The sample of 5.9 mg was stored in an Al2O3 crucible in nitrogen atmosphere and the rate of temperature change was 5 K min-1.

Simultaneous TG-DTA curves were obtained with thermal analysis system model Setaram Setsys 1200. The sample of 29.6 mg was stored in an Al2O3 crucible in nitrogen atmosphere and the rate of temperature change was 5 K min-1

Elemental analysis was made using an Elemental Model Vario EL III instrument.

DFT calculations

The DFT calculations were performed with the GAUSSIAN 09 program package [55]. The calculations employed the B3LYP exchange-correlation functional, which combines the hybrid exchange functional of Becke [56, 57] with the gradient-correlation functional of Lee et al. [58] and the split-valence polarized 6-311++G(d,p) basis set [59]. The basis set for iodine has been taken from the EMSI Basis Set Library [60, 61] created by Glukhovtsev et al. [62]. The geometries of molecules determined by X-ray diffraction were used as the starting models for the structure optimizations. All calculated IR frequencies are real, consistently with the minimum energies of the optimized structures.

Discussion

Crystal structure

The crystal structure of 3-(trimethylammonium)-benzoic acid iodide hydrate is composed of the 3-(trimethylammonium)-benzoic cation, iodide anion, and water molecules at the 1:1:1 ratio. This complex is remarkable in that it contains four independent formula units (Z’ = 4), as illustrated in Figs. 1 and 2.

Fig. 2.
figure 2

Autostereographic projection [63] of the crystal structure of 1, with the torsion angle C8-N1-C3-C2 indicated for 4 symmetry independent cations: letters A, B, C and D on the left side of the drawing indicate the rows of the independent cations along [z]. Pseudosymmetry elements have been indicated in yellow (screw axes 21) and inversion centers (purple circles).

Full size image

The crystal symmetry is of monoclinic space group Pc (model I), but it approximates a higher symmetry of space group P21/c (model II), and even still higher symmetry P21/c in the unit cell twice smaller along [x] (model III). This highly pseudosymmetric model III could be refined with anisotropic temperature factors to R 1 = 0.0718, but the water molecule appeared disordered in two positions and the thermal ellipsoids of the methyl were elongated (Z’ was equal to 1 for this pseudosymmetric model III); also the hydroxyl and carbonyl oxygen atoms of the carboxyl groups, as well as the carboxyl H atoms appeared disordered. The structure with the unit cell twice increased along [x] (as indicated by clearly observable, but considerably weaker reflections with odd h indices) still approximated the symmetry of space groups P21/c, with two symmetry-independent formula units (Z’ = 2). In this pseudosymmetric model II, the water molecules and the carboxyl groups became ordered, but one of independent cations had the methyls disordered. The R 1 factor for model II was 0.0637. Because the systematic absences of the 21 screw axes diverted slightly from zero intensities, we further reduced the model symmetry to space group Pc, which increased Z’ to 4, and fully eliminated the conformational disorder (model I). This model refined to the lowest residue factors (R 1 = 0.0594) and the lowest thermal displacement parameters. It also revealed subtle differences in the conformation of the carboxyl groups, as shown in Figs. 2 and 3, as well as the different orientations of trimethylammonium groups (Fig. 4).

Fig. 3.
figure 3

Torsion angles O1-C7-C1-C2 in symmetry independent molecules A (red), B (green), C (blue) and D (black) in the structure of 1, as a function of temperature.

Full size image
Fig. 4.
figure 4

Torsion angles C8-N1-C3-C2 describing the orientation of trimethylammonium groups in symmetry independent molecules A (red), B (green), C (blue) and D (black) in the structure of 1, as a function of temperature. The magnitudes for molecules B and C have been transformed to the positive values.

Full size image

According to the thermogravimetry (TG) measurements the compound 1 decomposes by losing water at 353 K, and at still higher temperature a series of transitions take place in the anhydrate. No phase transition in hydrate I has been detected between 160-353 K (see the TG and DSC signals in Figs. S3 and S4).

The low temperature structural studies showed no transitions either, and confirmed that the crystal remained in the Pc-symmetric phase with Z’ = 4 down to 130 K. Figure 5 shows the monotonic thermal expansion of the unit-cell parameters.

Fig. 5.
figure 5

Unit-cell dimensions of 1 plotted as a function of temperature: (a) parameters a, b and c; (b) angle β and (c) the unit-cell volume. The estimated standard deviations are smaller than the symbols.

Full size image

Four independent cations can be described as conformers due to different positions of trimethylammonium groups, as illustrated in Fig. 4. It can be observed that the positions of trimethylammonium groups in molecules A, B and D are similar within about 10° [i.e (10 ± 10)°], whereas the position of the group in molecule C is different by about 30°. The orientations of the trimethylammonium groups change within 10° between 300 and 130 K.

The carboxylic groups are bonded to the water molecule through the O(1)-H(1)∙∙∙O(1W), O(11)-H(11)∙∙∙O(2W), O(21)-H(21)∙∙∙O(3W) and O(31)-H(31)∙∙∙O(4W) hydrogen bonds Table 2, cf. Tables S2). The iodide anions are located close to the positively charged trimethylammonium groups, and distances are I(1)···N(1) 4.393(9), I(2)···N(2) 4.532(10), I(3)···N(3) 4.639(9) and I(4)···N(4) 4.421(8) Å.

Table 2. Experimental (1-model I) and calculated 2A and 2B by the B3LYP/6-311++G(d,p) approach, selected dimensions of hydrogen bonds and short contacts for 3-(trimethylammonium)-benzoic acid iodide hydrate (Å and °) at 296 K (cf. Table S2 in Supplementary Material)
Full size table

DFT calculations

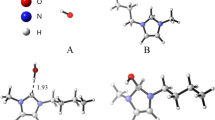
The starting molecular geometries for theoretical computations were adopted of cations A and B with their closest I- anions and water molecules. We have chosen the cations A and B for the calculations, because their conformation significantly differ in the position of the carboxyl group, whereas only minor differences in the positions of the trimethylammonium group is present in cations C and D. These two structures have been optimized as models 2A and 2B at the B3LYP/6-311++G(d,p) level of theory. As can be seen in the drawings of two optimized models 2A and 2B, shown in Fig. 6, their conformations well reproduce the opposite orientation of the carboxyl groups, this in cations A and C versus that in cations B and D. It is thus apparent that both conformations of the carboxyl group are very similar energetically and therefore they both can be present in the crystal structure. On the other hand it shows that the conformational differentiation is advantageous for the crystal packing.

Fig. 6.
figure 6

Computed structures of 2A and 2B of 3-(trimethylammonium)-benzoic acid iodide hydrate

Full size image

The optimized structures well represent the crystal ones. The O(1)-H(1)∙∙∙O(1W) hydrogen bond is slightly shorter in 2B than in 2A, similarly as in the crystal (Table 2). The calculated energies are E(a.u) = -7590.8511393 and dipole moment μ = 16.18 D for 2A, and E(a.u) = -7590.8508038 and dipole moment μ = 15.87 D for 2B. The energy of structure 2A is lower by 0.88 KJ/mol than that of structure 2B. The optimized structures differ significantly in the orientation of the carboxylic group and slightly in the N+∙∙∙I– distances, which are 4.082 in 2A and 4.092 Å in 2B. The torsion angles O1-C7-C1-C2 and C8-N1-C3-C2 describing the orientations of the carboxyl and trimethylammonium groups are 179.90 and 0.24° in model 2A and 0.09 and 0.11° in model 2B, respectively (cf. Figs 3 and 4).

FTIR spectrum

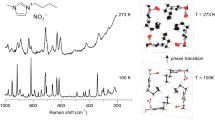
The solid-state spectrum of 3-(trimethylammonium)-benzoic acid iodide hydrate shown in Fig. 7 is consistent with the structure of 1. The band at 3447 cm-1 with a shoulder at 3555 cm-1 is attributed to the stretching vibration O(1W)-H(W) of water molecule. The broad absorption in the 3000-2000 cm-1 region is attributed to the νO(1)-H(1)∙∙∙O(1W) hydrogen bond vibration. It is typical for O-H∙∙∙O hydrogen bond of the length of ca. 2.6 Å. The splitting band at 1722 and 1704 cm-1 can be assigned to νCO modes in independent cations, while the intensive band at 1258 cm-1 to the δCO and δOH vibrations.

Fig. 7.
figure 7

(a) The solid-state FTIR spectrum of 3-(trimethylammonium)-benzoic acid iodide hydrate (1) and (b) the calculated, by the B3LYP/6-311++G(d,p) approach, spectra of 2A (black line) and 2B (red line).

Full size image

The calculated IR spectra of 2A and 2B, in vertical lines, are shown in Fig. 7b (the spectrum of 2A in black line and 2B in red line). The differences between the calculated and experimental frequencies follow from the fact that the experimental spectrum was recorded for the compound in solid state, while the computations were made for the vibrations of isolated molecule in gas phase. The calculated bands are shifted to higher wavenumbers relative to the experimental data, because the calculations are based on harmonic frequency, while the experimental ones are based on the anharmonic frequencies. In the computed theoretically IR spectra of 2A and 2B optimized structures the ν asO(1W)-H(W) and ν sO(1W)-H(W) bands are predicted at 3872 and 3696 cm-1, respectively. The νO(1)-H(1) mode is predicted at 3223 cm-1 in both spectra. The differences in the spectra of 2A and 2B are observed in the carboxylic group region. The νCO, δCO and δOH vibrations are calculated at 1764 and 1315 cm-1, respectively for 2A, whereas at 1770 and 1306 cm-1, respectively for 2B. The bands at 980 and 978 cm-1 are predicted to the γO(1)-H(1) vibrations in the spectra of 2A and 2B. The band at 611 cm−1 is calculated for γO(1W)-H(W) mode.

Conclusions

The high pseudosymmetry of crystal 1 can be attributed to the conformational freedom in the cations, where two opposite orientations of the carboxyl groups hardly change the potential energy of the cation. It discriminates the cations and also affects the positions of H-bonded water molecules. However the origin of further differentiation of the cations, by the orientations of trimethylammonium groups remains puzzling, particularly that this soft conformational parameter breaks the symmetry of inversion center. In the terms of crystal engineering, such a change could be most required for producing non-centrosymmetric crystals for second harmonic generation and other applications. It occurred that the crystals of 1 are quite stable and no transitions to any of higher-symmetric models II and III (both centrosymmetric) could be detected. It testifies that the factors differentiating the conformers are significant and their identification would significantly contribute to understanding of the rules governing the symmetry of molecules crystals.