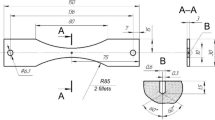
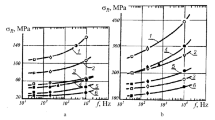
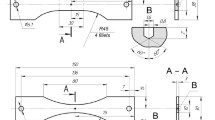
A methodology for theoretically estimating the endurance limit of a material for conditions of multicycle fatigue is proposed. The estimation is based on the fact that under these conditions, a nonpropagating surface fatigue crack of one grain size exists at the level of the applied stress range equal to the endurance limit. In this regard, the tools of linear-elastic fracture mechanics were used in the development of the methodology, but with corrections for the size and geometry of a short fatigue crack. The methodology allows for estimating the endurance limit of smooth specimens under symmetric and positive stress ratios of the loading cycle. The initial data for the estimation are the characteristics of the static strength and microstructure of the material. The reliability of the proposed estimation is confirmed by experimental fatigue data for structural alloys of various classes taken from the literature.






Similar content being viewed by others
References
ASTM E466-15. Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials (2015).
O. M. Herasymchuk, “Nonlinear relationship between the fatigue limit and quantitative parameters of material microstructure,” Int. J. Fatigue, 33, 649–659 (2011).
M. D. Chapetti, “Fatigue propagation threshold of short cracks under constant amplitude loading,” Int. J. Fatigue, 25, 1319–1326 (2003).
M. H. El Haddad, T. H. Topper, and K. N. Smith, “Prediction of non propagating cracks,” Eng. Fract. Mech., 11, No. 3, 573–584 (1979).
A. J. McEvily, M. Endo, and Y. Murakami, “On the \(\sqrt{area}\) relationship and the short fatigue threshold,” Fatigue Fract. Eng. Mater. Struct., 26, 269–278 (2003).
ASTM E647-00. Standard Test Method for Measurements of Fatigue Crack Growth Rates (2000).
H. Kitagawa and S. Takahashi, “Applicability of fracture mechanics to very small cracks or the cracks in the early stage,” in: Proc. of the Second Int. Conf. of Mechanical Behavior of Materials, ASM, Metals Park, OH (1976), pp. 627–631.
U. Krupp, Fatigue Crack Propagation in Metals and Alloys: Microstructural Aspects and Modelling Concepts, Wiley-VCH, Weinheim (2007).
R. W. Hertzberg, “A simple calculation of \(da/dN-\Delta K\) data in the near threshold regime and above,” Int. J. Fracture, 64, 53–58 (1993).
O. M. Herasymchuk, “Microstructurally-dependent model for predicting the kinetics of physically small and long fatigue crack growth,” Int. J. Fatigue, 81, 148–161 (2015).
J. P. Lukas and W. W. Gerberich, “A proposed criterion for fatigue threshold: dislocation substructure approach,” Fatigue Fract. Eng. Mater. Struct., 6, 271–280 (1983).
T. Hanlon, E. D. Tabachnikova, and S. Suresh, “Fatigue behavior of nanocrystalline metals and alloys,” Int. J. Fatigue, 27, 1147–1158 (2005).
O. M. Herasymchuk, O. V. Kononuchenko, P. E. Markovsky, and V. I. Bondarchuk, “Calculating the fatigue life of smooth specimens of two-phase titanium alloys subject to symmetric uniaxial cyclic load of constant amplitude,” Int. J. Fatigue, 83, 313–322 (2016).
J. O. Peters, B. L. Boyce, X. Chen, et al., “On the application of the Kitagawa–Takahashi diagram to foreign-object damage and high-cycle fatigue,” Eng. Fract. Mech., 69, 1425–1446 (2002).
O. M. Herasymchuk and O. V. Kononuchenko, “Peculiarities of short fatigue cracks growth from a blind hole in specimens made of steel 45. Part 1. Experimental results,” Strength Mater., 53, No. 2, 213–221 (2021). https://doi.org/10.1007/s11223-021-00277-z
K. Tanaka, Y. Nakai, and Y. Yamashita, “Fatigue growth threshold of small cracks,” Int. J. Fracture, 17, No. 5, 519–533 (1981).
J. S. Park, S. J. Kim, K. H. Kim, et al., “A microstructural model for predicting high cycle fatigue life of steels,” Int. J. Fatigue, 27, 1115–1123 (2005).
D. N. Hanlon and W. M. Rainforth, “Some observations on cyclic deformation structures in the high-strength commercial aluminum alloy AA 7150,” Metall. Mater. Trans. A, 29, 2727–2736 (1998).
Y. Akiniwa and K. Tanaka, “Statistical characteristics of propagation of small fatigue crack in smooth specimens of aluminium alloy 2024-T3,” Mater. Sci. Eng. A, 104,105–115 (1988).
K. Tokaji, M. Kamakura, Y. Ishiizumi, and N. Hasegawa, “Fatigue behaviour and fracture mechanism of a rolled AZ31 magnesium alloy,” Int. J. Fatigue, 26, 1217–1224 (2004).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Problemy Mitsnosti, No. 1, pp. 33 – 44, January – February, 2023.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Herasymchuk, O.M. Theoretical Estimation of the Endurance Limit of Metal Materials by the Characteristics of Their Static Strength and Microstructure Based on the Linear-Elastic Fracture Mechanics. Strength Mater 55, 25–34 (2023). https://doi.org/10.1007/s11223-023-00499-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11223-023-00499-3