Skip to main content
SpringerLink
Log in

Crack identification in reinforced concrete beams using ANSYS software

  • Published:
Strength of Materials Aims and scope

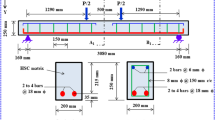
Three-dimensional nonlinear finite element model of reinforced concrete beam has been developed in this study. The general purpose finite element package, ANSYS 8.0, is employed for the numerical analyses. Using SOLID65 solid elements, the compressive crushing of concrete is facilitated using plasticity algorithm while the concrete cracking in tension zone is accommodated by the nonlinear material model. Smeared reinforcement is used and introduced as a percentage of steel embedded in concrete. Comparison with hand calculated results is presented for the concrete beam. Convergence of analytical results is showed. The capability of the model to capture the critical crack regions, loads and deflections for various types of loadings in reinforced concrete beam has been illustrated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Y. H. Bangash, Concrete and Concrete Structures: Numerical Modeling and Applications, Elsevier Science Publishers Ltd., London (1989).

    Google Scholar 

  2. Y. Hemmaty, “Modeling of the shear force transferred between cracks in reinforced and fibre reinforced concrete structures,” in: Proc. of the ANSYS Conf., Vol. 1, Pittsburgh, PA (1998).

  3. ANSYS 8.0 Manual Set, ANSYS Inc., Canonsburg, PA (1998).

  4. ANSYS Theory Reference, Seventh Edition, Swanson Analysis Systems (1998).

  5. ANSYS – Engineering Analysis System. Theoretical Manual (for ANSYS Revision 8.04), Swanson Analysis Systems (1998).

  6. D. Kachlakev and T. Miller, FE Modeling of Reinforced Concrete Structures Strengthened with FRP Lamiates, Final Report SPR 316, Oregon State University (2001).

  7. K. J. Willam, University of Colorado (Private communication) (1982).

  8. K. J. William and E. D. Warnke, “Constitutive model for the triaxial behavior of concrete,” in: Proc. of the Int. Association for Bridge and Structural Engineering, ISMES, Bergamo (1975), Vol. 19, p. 174.

  9. K. J. Bathe, Finite Element Procedures, Prentice-Hall Inc., New Jersey (1996).

    Google Scholar 

  10. W. F. Chen and D. J. Han, Plasticity for Structural Engineers, Springer-Verlag, New York (1988).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mouloud Mammeri University, Tizi-Ouzou, Algeria

    L. Dahmani & S. Kaci

  2. University of Southern Queensland, Toowoomba, Australia

    A. Khennane

Authors
  1. L. Dahmani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Khennane
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Kaci
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Problemy Prochnosti, No. 2, pp. 141 – 153, March – April, 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dahmani, L., Khennane, A. & Kaci, S. Crack identification in reinforced concrete beams using ANSYS software. Strength Mater 42, 232–240 (2010). https://doi.org/10.1007/s11223-010-9212-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11223-010-9212-6

Keywords

Search

Navigation