Unbiased approximation of posteriors via coupled particle Markov chain Monte Carlo

Abstract

Markov chain Monte Carlo (MCMC) is a powerful methodology for the approximation of posterior distributions. However, the iterative nature of MCMC does not naturally facilitate its use with modern highly parallel computation on HPC and cloud environments. Another concern is the identification of the bias and Monte Carlo error of produced averages. The above have prompted the recent development of fully (‘embarrassingly’) parallel unbiased Monte Carlo methodology based on coupling of MCMC algorithms. A caveat is that formulation of effective coupling is typically not trivial and requires model-specific technical effort. We propose coupling of MCMC chains deriving from sequential Monte Carlo (SMC) by considering adaptive SMC methods in combination with recent advances in unbiased estimation for state-space models. Coupling is then achieved at the SMC level and is, in principle, not problem-specific. The resulting methodology enjoys desirable theoretical properties. A central motivation is to extend unbiased MCMC to more challenging targets compared to the ones typically considered in the relevant literature. We illustrate the effectiveness of the algorithm via application to two complex statistical models: (i) horseshoe regression; (ii) Gaussian graphical models.

Appendices

A Systematic resampling

Algorithms 7 through 9 detail the systematic resampling methods used for the empirical results derived from Algorithm 6. They involve the floor function denoted by $\lfloor x\rfloor$, i.e., $\lfloor x\rfloor$ is the largest integer for which $\lfloor x\rfloor \le x$.

B Proofs for Section 4

Our results derive from Lee et al. (2020). They consider a smoothing set-up which maps to our context of approximating a general posterior $\pi (x)$ using adaptive SMC. Specifically, their target density is (Lee et al. 2020, Equation 1)

$$\begin{aligned} \Pi (x_{0:S}) \propto M_0(x_0)\, G_0(x_0)\ \prod _{s=1}^S M_s(x_{s-1}, x_s)\, G_s(x_{s-1},x_s). \end{aligned}$$

(4)

In our context, the term $M_0(x)=\pi _{\alpha _0}(x)$ is a tempered posterior, the term $G_0(x) = {p(y\mid x)}^{\alpha _1 - \alpha _{0}}$ a tempered likelihood, $M_s(x_{s-1}, x_s)$ the density of the Markov transition starting at $x_{s-1}$ resulting from the $m_s$ MCMC steps which are invariant w.r.t. $\pi _{\alpha _s}(x)$ in Step 2c of Algorithm 2 for $s=1,\dots ,S$, $G_s(x_{s-1}, x_s) = {p(y\mid x_s)}^{\alpha _{s+1} - \alpha _{s}}$ a tempered likelihood for $s=1,\dots ,S-1$, and $G_S(x_{S-1}, x_S) = {p(y\mid x_S)}^{1 - \alpha _{S}}$ a tempered likelihood. Then, the coupled conditional particle filter in Algorithm 2 of Lee et al. (2020) reduces to the coupled conditional SMC in our Algorithm 4. Thus, the results in Lee et al. (2020) apply to Algorithm 4.

1.1 B.1 Proof of Proposition 1

Since $G_s(x_{s-1}, x_s)$ does not depend on $x_{s-1}$, we can write $G_s(x_{s-1}, x_s) = G(x_s)$ for $s=1,\dots ,S$ as in Section 2 of Lee et al. (2020). Assumption 1, that ${p(y\mid x)}$ is bounded, implies that $G_s(x_s)$ is bounded for $s=0,\dots ,S$, which is Assumption 1 in Lee et al. (2020). Therefore, Theorem 8 of Lee et al. (2020) provides $\mathrm {Pr}(x_{0:S}' = {\bar{x}}_{0:S}') \ge N/(N+c).$

Part (iii) follows similarly to the proof for Theorem 10(iii) of Lee et al. (2020): We have $\mathrm {Pr}(\tau > t) \le \{1 - N/(N+c)\}^{t-1}$ for $t\ge 1$. Therefore,

$$\begin{aligned} \begin{aligned} E(\tau ) = \sum _{t=0}^\infty \mathrm {Pr}(\tau> t)&\le 1 + \sum _{t=1}^\infty \mathrm {Pr}(\tau > t) \\&\le 1 + \sum _{t=1}^\infty \left( 1 - \frac{N}{N+c} \right) ^{t-1} \\&= 2 + \frac{c}{N}, \end{aligned} \end{aligned}$$

where the last equality follows from the geometric series formula $\sum _{t=0}^\infty (1 - r)^t = 1/r$ for $|r|<1$. Part (iii) implies Part (ii). $\square$

1.2 Proof of Proposition 2

Theorem 10 of Lee et al. (2020) provides results for a statistic that we denote by $h_{0:S}: {\mathcal {X}}^{S+1}\rightarrow {\mathbb {R}}$. Consider $h_{0:S}$ defined by $h_{0:S}(x_{0:S})=h(x_S)$ where $h:{\mathcal {X}}\rightarrow {\mathbb {R}}$ is our statistic of interest. Then, $h_{0:S}$ is bounded by Assumption 2. The marginal distribution of $x_S$ under the density on $x_{0:S}$ in (4) is our posterior of interest $\pi (x)$. Consequently, the results for $h_{0:S}$ in Theorem 10 of Lee et al. (2020) provide the required results for h. $\square$

C Comparison with coupled HMC

The coupled HMC method of Heng and Jacob (2019) provides an alternative to coupled particle MCMC for unbiased posterior approximation if the posterior is amenable to HMC. The latter typically requires ${\mathcal {X}} = {\mathbb {R}}^{d_x}$ and that the posterior is continuously differentiable. Here, we apply coupled HMC to the posterior considered in Sect. 5.1 with a slight modification to make it suitable for HMC: the uniform prior over the hypercube $[-10, 10]^{d_x}$ is replaced by the improper prior $p(x)\propto 1$ for $x\in {\mathbb {R}}^{d_x}$ to ensure differentiability. The set-up of coupled HMC follows Section 5.2 of Heng and Jacob (2019) with the following differences. The leap-frog step size is set to 0.1 instead of 1 as the resulting MCMC failed to accept with the latter. We do not initialize both chains independently but instead set ${\bar{x}}(1)= x(0)$ as in Algorithm 6 since we found that this change reduces meeting times. We use code from https://github.com/pierrejacob/debiasedhmc to implement the method from Heng and Jacob (2019).

Fig. 5

Results from execution of coupled HMC from Heng and Jacob (2019) for the case of the mixture of Gaussians, under the adjustments described in Appendix C. The top row contains a violin plot of $\log (\tau )$. The bottom two rows show the integrated autocorrelation time and ${\hat{{{\,\mathrm{var}\,}}}}({\bar{h}}_k^l)\times \text {time}$ as a function of l, with their means and 95% bootstrapped confidence intervals in black and gray, respectively

Figure 5 presents the results analogously to Fig. 1. In terms of number of iterations, coupled HMC mixes worse and takes longer to meet than coupled particle MCMC. These increases are not offset by a lower computational cost per iteration. An important caveat here is that computation time depends on the implementation, and here coupled HMC is implemented using an R package and coupled particle MCMC in Python.

D Additional simulations studies

Here, we provide some further simulation studies where the set-up is the same as in Sect. 5.1 except for the following. We consider a probability of PIMH of $\rho = 0.05$ in addition to the other values of $\rho$, the maximum l is $l_{\max }=2\cdot 10^3$ and the number of repetitions is $R=128$. Figure 8 considers different number of particles of N. Figure 9 varies the dimensionality of the parameter $d_x$ where we use the true values $x^* = (-3, 0, 3)^\top$ and $x^* = (-3, 0, 3, 6)^\top$ for $d_x=3$ and $d_x=4$, respectively, based on the set-up in Middleton et al. (2019, Appendix B.2). Additionally, Fig. 9b uses independent inner MCMC steps across both chains except for that the MCMC step is faithful to any coupling. This contrasts with Sect. 5.1 which uses a common random number coupling for the Metropolis-Hastings inner MCMC step.

A higher number of particles N results in shorter meeting times. Criterion ‘${\hat{{{\,\mathrm{var}\,}}}}({\bar{h}}_k^l)\times \text {time}$’ is lowest for larger N, though beyond a certain N, not much improvement is gained. Jacob et al. (2020a) reach a similar conclusion when varying N for coupled conditional particle filters.

Performance deteriorates with increasing dimensionality $d_x$, especially for smaller values of $\rho$. For $d_x=4$ (Fig. 9d), the chains even often fail to meet within the maximum number of iterations of 2000 considered for $\rho =0,0.05$. We also see such lack of coupling in Fig. 9b for $\rho =0$, suggesting that the coupling of the inner MCMC is important for good performance when working with coupled conditional SMC. This is despite the fact that the theoretical results in Sect. 4 do not depend on the quality of the coupling of the inner MCMC.

For certain values of l, using $\rho$ away from 0 or 1 is competitive with conditional SMC or PIMH in terms of ‘${\hat{{{\,\mathrm{var}\,}}}}({\bar{h}}_k^l)\times \text {time}$’ although not notably better than using just one of them. The benefit of a mixture versus using only conditional SMC in terms of coupling is highlighted in Fig. 9b where the inner MCMC is uncoupled.

E Inner MCMC step for Gaussian graphical models

We set up an MCMC step with $p(x\mid y) = p(K,G\mid Y)$ as invariant distribution. The corresponding MCMC step for the tempered density ${p_\alpha (x\mid y)}$, $\alpha \in (0,1]$, required for Algorithm 6, follows by replacing n and U by $\alpha n$ and $\alpha U$, respectively, as $p(y\mid x)^\alpha =$

$(2\pi )^{-\alpha np/2}|K|^{\alpha n/2} \exp (-\frac{1}{2}\left<K, \alpha U\right>)$. We make use of the algorithm for sampling from a G-Wishart law introduced in Lenkoski (2013, Section 2.4). Thus, we can sample from ${K\mid G, Y} \sim {\mathcal {W}}_G(\delta +n,\, D^*)$. It remains to derive an MCMC transition that preserves $p(G\mid Y)$, as samples of G can be extended to $x=(K,G)$ by generating $K\mid G, Y$.

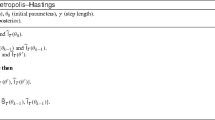
We consider the double reversible jump approach from Lenkoski (2013) and apply the node reordering from Cheng and Lenkoski (2012, Section 2.2) to obtain an MCMC step with no tuning parameters. The MCMC step is a Metropolis-Hastings algorithm on an enlarged space that bypasses the evaluation of the intractable normalisation constants $I_G(\delta , D)$ and $I_G(\delta +n,\, D^*)$ in the target distribution (3). It is a combination of ideas from the PAS algorithm of Godsill (2001), which avoids the evaluation of $I_G(\delta +n,\, D^*)$, and the exchange algorithm of Murray et al. (2006), which sidesteps evaluation of $I_G(\delta , D)$. We will give a brief presentation of the MCMC kernel that we are using as it does not coincide with approaches that have appeared in the literature.

Fig. 6

The enlarged hierarchical model giving rise to a posterior on an extended space that will be preserved by our MCMC kernel. The construction aims at: (i) removing the requirement for calculation of intractable normalising constants; (ii) avoiding introducing tuning parameters. The main text defines $\Phi =(\Phi _{-f}, \Phi _{p-1,p})$ and ${\tilde{\Phi }}=({\tilde{\Phi }}_{-f}, {\tilde{\Phi }}_{p-1,p})$

To attain the objective of suppressing the normalising constants in the method, one works with a posterior on an extended space, defined via the directed acyclic graph in Fig. 6. The left side of the graph gives rise to the original posterior $p(G)\, p(K\mid G)\, p(Y\mid K)$. Denote by ${\tilde{G}}$ the proposed graph, with law $q({\tilde{G}}\mid G)$. Lenkoski (2013) chooses a pair of vertices (i, j) in G, $i<j$, at random and applies a reversal, i.e. $(i,j)\in {\tilde{G}}$ if and only if $(i,j)\notin G$. The downside is that the probability of removing an edge is proportional to the number of edges in G, which is typically small. Instead, we consider the method in Dobra et al. (2011, Equation A.1) that also applies the reversal, but chooses (i, j) so that the probabilities of adding and removing an edge are equal.

We reorder the nodes of G and ${\tilde{G}}$ so that the edge that has been altered is $(p-1,p)$, similarly to Cheng and Lenkoski (2012, Section 2.2). Given ${\tilde{G}}$, the graph in Fig. 6 contains a final node that refers to the conditional distribution of $p({\tilde{K}}\mid {\tilde{G}})$ which coincides with the G-Wishart prior $p(K\mid G)$. Consider the upper triangular Cholesky decomposition $\Phi$ of K so that $\Phi ^\top \Phi = K$. Let $\Phi _{-f} = \Phi \setminus \Phi _{p-1,p}$. We work with the map $K \leftrightarrow \Phi =(\Phi _{-f}, \Phi _{p-1,p})$. We apply a similar decomposition for ${\tilde{K}}$, and obtain the map ${\tilde{K}} \leftrightarrow {\tilde{\Phi }}=({\tilde{\Phi }}_{-f}, {\tilde{\Phi }}_{p-1,p})$.

We can now define the target posterior on the extended space as

$$\begin{aligned} p\big (G, {\tilde{G}}, \Phi _{p-1,p}, {\tilde{\Phi }}_{p-1,p} \mid \Phi _{-f}, {\tilde{\Phi }}_{-f}, Y\big ) \\ \propto p\big (G)\,q({\tilde{G}}\mid G)\,p(\Phi \mid G)\,p({\tilde{\Phi }}\mid {\tilde{G}})\,p(Y\mid \Phi ). \end{aligned}$$

(5)

Given a graph G, the current state on the extended space comprises of

$$\begin{aligned} \big (G, {\tilde{G}}, \Phi _{-f}, \Phi _{p-1,p}, {\tilde{\Phi }}_{-f}, {\tilde{\Phi }}_{p-1,p}\big ), \end{aligned}$$

(6)

with ${\tilde{G}}\sim q({\tilde{G}}\mid G)$, and $\Phi$, ${\tilde{\Phi }}$ obtained from the Cholesky decomposition of the precision matrices $K\sim {\mathcal {W}}_G(\delta +n, D^{*})$, ${\tilde{K}} \sim {\mathcal {W}}_{{\tilde{G}}}(\delta , D)$, respectively. Note that the rows and columns of D, $D^{*}$ have been accordingly reordered to agree with the re-arrangement of the nodes we describe above. Consider the scenario with the proposed graph ${\tilde{G}}$ having one more edge than G. Given the current state in (6), the algorithm proposes a move to the state

$$\begin{aligned} \big ({\tilde{G}},G, \Phi _{-f}, \Phi ^\text {pr}_{p-1,p}, {\tilde{\Phi }}_{-f}, {\tilde{\Phi }}^\text {pr}_{p-1,p}\big ). \end{aligned}$$

(7)

The value $\Phi ^\text {pr}_{p-1,p}$ is sampled from the conditional law of ${\Phi }_{p-1,p}\mid {\Phi }_{-f}, Y$.

We provide here some justification for the above construction. The main points are the following: (i) the proposal corresponds to an exchange of $G\leftrightarrow {\tilde{G}}$, coupled with a suggested value for the newly ‘freed’ matrix element $\Phi ^\text {pr}_{p-1,p}$; (ii) from standard properties of the general exchange algorithm, switching the position of $G, {\tilde{G}}$ will cancel out the normalising constants of the G-Wishart prior from the acceptance probability; (iii) the normalising constants of the G-Wishart posterior never appear, as the precision matrices are not integrated out.

Fig. 7

Posterior edge inclusion probabilities for the Gaussian graphical model fit on the metabolite data from SMC with $N=10^5$ particles (upper triangle) and their absolute difference from the estimates from coupled particle MCMC in Fig. 3 (lower triangle). LDL, HDL and FA stand for low-density lipoprotein, high-density lipoprotein and fatty acids, respectively

Fig. 8

Results from execution of Algorithm 6 with $\rho =0$ (conditional SMC), $\rho = 0.05$, $\rho = 0.5$ and $\rho = 1$ (PIMH), for the case of the mixture of Gaussians for various number of particles N. The top row contains violin plots of $\log (\tau )$. The bottom two rows show the integrated autocorrelation time and ${\hat{{{\,\mathrm{var}\,}}}}({\bar{h}}_k^l)\times \text {time}$ as a function of l, with their means and 95% bootstrapped confidence intervals in black and gray, respectively

Fig. 9

Results from execution of Algorithm 6 with $\rho =0$ (conditional SMC), $\rho = 0.05$, $\rho = 0.5$ and $\rho = 1$ (PIMH), for the case of the mixture of Gaussians for various parameter dimensionalities $d_x$ and, in (b), for when the inner MCMC steps are not coupled beyond being faithful. The top row contains violin plots of $\log (\tau )$. The bottom two rows show the integrated autocorrelation time and ${\hat{{{\,\mathrm{var}\,}}}}({\bar{h}}_k^l)\times \text {time}$ as a function of l, with their means and 95% bootstrapped confidence intervals in black and gray, respectively

Appendix F derives that

$$\begin{aligned} {\Phi }_{p-1,p}\mid {\Phi }_{-f}, Y \sim {\mathcal {N}}\left( \frac{-D^*_{p-1,p} {\Phi }_{p-1,p-1}}{D^*_{p,p}},\, \frac{1}{D^*_{p,p}} \right) \end{aligned}$$

(8)

This avoids the tuning of a step-size parameter arising in the Gaussian proposal of Lenkoski (2013, Section 3.2). The variable ${\tilde{\Phi }}^\text {pr}_{p-1,p}$ is not free, due to the edge $(p-1,p)$ assumed being removed, and is given as (Roverato 2002, Equation 10)

$$\begin{aligned} {\tilde{\Phi }}^\text {pr}_{p-1,p} = - \sum _{i=1}^{p-2} {\tilde{\Phi }}_{i,p-1}{\tilde{\Phi }}_{ip} / {\tilde{\Phi }}_{p-1,p-1} \end{aligned}$$

The acceptance probability of the proposal is given in Step 6 of the complete MCMC transition shown in Algorithm 10 for exponent $\epsilon =1$. In the opposite scenario when an edge is removed from G, then, after again re-ordering the nodes, the proposal ${\tilde{\Phi }}^\text {pr}_{p-1,p}$ is sampled from

$$\begin{aligned} {\tilde{\Phi }}_{p-1,p}\mid {\tilde{\Phi }}_{-f} \sim {\mathcal {N}}\left( \frac{-D_{p-1,p} {\tilde{\Phi }}_{p-1,p-1}}{ D_{p,p}},\, \frac{1}{D_{p,p}} \right) \end{aligned}$$

whereas we fix $\Phi _{p-1,p}^\text {pr} = - \sum _{i=1}^{p-2} \Phi _{i,p-1}\Phi _{ip} /\Phi _{p-1,p-1}$. The corresponding acceptance probability for the proposed move is again as in Step 6 of Algorithm 10, but now for $\epsilon =-1$.

F Proposal for precision matrices

This derivation is similar to Appendix A of Cheng and Lenkoski (2012). Assume that the edge $(p-1,p)$ is in the proposed graph ${\tilde{G}}$ but not in G. The prior on ${\tilde{\Phi }}_{p-1,p}\mid {\tilde{\Phi }}_{-f}$ follows from Equation 2 of Cheng and Lenkoski (2012) as

$$\begin{aligned} p({\tilde{\Phi }}_{p-1,p}\mid {\tilde{\Phi }}_{-f},{\tilde{G}}) \propto \exp \left( -\frac{1}{2} \langle {\tilde{\Phi }}^\top {\tilde{\Phi }}, D\rangle \right) . \end{aligned}$$

The likelihood is

$$\begin{aligned} p(Y\mid {\tilde{K}}) \propto |{\tilde{K}}|^{n/2} \exp \left( -\frac{1}{2} \langle {\tilde{K}}, U\rangle \right) . \end{aligned}$$

Here, $|{\tilde{K}}|$ does not depend on ${\tilde{\Phi }}_{p-1,p}$ since $|{\tilde{K}}| = |{\tilde{\Phi }}|^2 = (\prod _{i=1}^p {\tilde{\Phi }}_{ii})^2$. Combining the previous two displays thus yields $p({\tilde{\Phi }}_{p-1,p}\mid {\tilde{\Phi }}_{-f},Y) \propto \exp ( -\langle {\tilde{\Phi }}^\top {\tilde{\Phi }}, D^*\rangle / 2)$. Dropping terms not involving ${\tilde{\Phi }}_{p-1,p}$ yields (8).

G Comparison with SMC for the metabolite application

We compare the results in Fig. 3 with those from running the SMC in Algorithm 2 with a large number of particles $N=10^5$. Comparing Figs. 3 and 7 shows that the results are largely the same. The edge probabilities for which they differ substantially are harder to estimate according to the Monte Carlo standard errors from coupled particle SMC in Fig. 3.