Skip to main content
SpringerLink
Log in

A flexible statistical and efficient computational approach to object location applied to electrical tomography

  • Published:
Statistics and Computing Aims and scope Submit manuscript

Abstract

In electrical tomography, multiple measurements of voltage are taken between electrodes on the boundary of a region with the aim of investigating the electrical conductivity distribution within the region. The relationship between conductivity and voltage is governed by an elliptic partial differential equation derived from Maxwell’s equations. Recent statistical approaches, combining Bayesian methods with Markov chain Monte Carlo (MCMC) algorithms, allow to greater flexibility than classical inverse solution approaches and require only the calculation of voltages from a conductivity distribution. However, solution of this forward problem still requires the use of the Finite Difference Method (FDM) or the Finite Element Method (FEM) and many thousands of forward solutions are needed which strains practical feasibility.

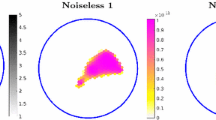
Many tomographic applications involve locating the perimeter of some homogeneous conductivity objects embedded in a homogeneous background. It is possible to exploit this type of structure using the Boundary Element Method (BEM) to provide a computationally efficient alternative forward solution technique. A geometric model is then used to define the region boundary, with priors on boundary smoothness and on the range of feasible conductivity values. This paper investigates the use of a BEM/MCMC approach for electrical resistance tomography (ERT) data. The efficiency of the boundary-element method coupled with the flexibility of the MCMC technique gives a promising new approach to object identification in electrical tomography. Simulated ERT data are used to illustrate the procedures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Besag J., Green P.J., Higdon D., and Mengersen K. 1995. Bayesian computation and stochastic systems. Statistical Science 10: 1–41.

    MATH  MathSciNet  Google Scholar 

  • Brebbia C.A., Telles J.C.F., and Wrobel L.C. 1984. Boundary Element Techniques: Theory and Applications. New York, USA, Springer-Verlag.

    Google Scholar 

  • Cheney M., Isaacson D., and Newell J.C. 1999. Electrical impedance tomography. SIAM Review 41: 85–101.

    Article  MATH  MathSciNet  Google Scholar 

  • Duraiswami R., Chahine G.L., and Sarkar K. 1997. Boundary element techniques for efficient 2-D and 3-D electrical impedance tomography. Chem. Eng. Sci. 52: 2185–2196.

    Article  Google Scholar 

  • Garabedian P.R. 1964. Partial Differential Equations. London, UK, AMS Chelsea Publishing.

  • Hanselman D. and Littlefield, D. 2001. Mastering Matlab 6—A Comprehensive Tutorial and Reference. New Jersey, USA, Prentice and Hall.

    Google Scholar 

  • Hoyle B. 2004. Industrial process tomography progress. In: Proceedings of the 3rd International Symposium on Process Tomography in Poland, Lodz, Poland, pp. 9.

  • Ider Y.Z., Gencer N.G., Atalar E., and Tosun H. 2004. Electrical impedance tomography of translationally uniform cylindrical objects with general cross-sectional boundaries. IEEE Trans. Medical Imaging 9: 49–59.

    Article  Google Scholar 

  • Jaswon M.A. and Symm G.T. 1977. Integral Equation Methods in Potential Theory and Electrostatics. London, Academic Press.

    Google Scholar 

  • Katsikadelis J.T. 2002. Boundary Elements: Theory and Applications. Elsevier Science.

  • Liu J.S. 2001. Monte Carlo Strategies in Scientific Computing. Berlin, Springer-Verlag.

  • Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller, A.H., and Teller E. 1953. Equations of state calculations by fast computing machine. J. Chem. Phys. (1953) 21: 1087–1091.

    Article  Google Scholar 

  • Spiegel M.R. 1974. Theory and problems of vector analysis. Schaum’s Outline Series. New York, USA, McGraw–Hill book company.

    Google Scholar 

  • Somersalo E., Cheney M., and Cheney D. 1992. Existence and uniqueness for electrode models fore electric computed tomography. SIAM J. Appl. Math. 52: 1023–40.

    Article  MATH  MathSciNet  Google Scholar 

  • Stitt E.H. and James K. 2003. Process tomography and particle tracking: Research tool and commercial diagnostic tool. In: Proceedings of the 3rd World Congress on Industrial Process Tomography, Banff, Canada.

  • Vilhunen T., Kaipio J.P., Vauhkonen P.J., Savolainen T., and Vauhkonen M. 2002. Simultaneous reconstruction of electrode contact impedances and internal electrical properties: I. Theory. Meas. Sci. Technol. 13: 1848–1854.

    Article  Google Scholar 

  • West R.M., Aykroyd R.G., Meng S., and Williams R.A. 2004. Markov Chain Monte Carlo techniques and spatial-temporal modelling for medical EIT. Physiological Measurements 25: 181–194.

    Article  Google Scholar 

  • West R.M., Meng S., Aykroyd R.G., and Williams R.A. 2005. Spatial-temporal modelling for EIT of a mixing process. Review of Scientific Instruments 76: 3703/1–10.

    Google Scholar 

  • Wrobel L.C. 2002. The Boundary-Element Method: volume 1, Applications in Thermo-Fluids and Acoustics. John Wiley publishers.

Download references

Author information

Authors and Affiliations

  1. Department of Statistics, University of Leeds, Leeds, LS2 9JT, UK

    Robert G. Aykroyd

  2. Department of Applied Mathematics, University of Leeds, Leeds, LS2 9JT, UK

    Brain A. Cattle

Authors
  1. Robert G. Aykroyd
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brain A. Cattle
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robert G. Aykroyd.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Aykroyd, R.G., Cattle, B.A. A flexible statistical and efficient computational approach to object location applied to electrical tomography. Stat Comput 16, 363–375 (2006). https://doi.org/10.1007/s11222-006-9619-x

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11222-006-9619-x

Keywords

Search

Navigation