1 Introduction

In the general understanding of flare/coronal mass ejection (CME) occurrences, the events must follow a “buildup and release” (BUR) pattern, in which slow subphotospheric stresses on the magnetic field drive essentially direct currents (DC) into the solar corona, which then restructure suddenly into a flare and/or a CME eruption. The stress could reflect simple energy build-up and release, or other physical parameters such as helicity.

In other astrophysical contexts, clear “relaxation oscillator” (Van der Pol and Van der Mark, 1927) behavior does appear. These include objects such as the X-ray bursts of the accreting binary system (e.g. Lamb, 1984) called the “rapid burster” (Lewin et al., 1976) and the timing glitches of the pulsar PSR J0537-6910 (Middleditch et al., 2006). Both of these objects show events with distinct correlations between the time after a given event, and the event magnitude in some measure. Note that two different forms of BUR could happen: a “reset” form, in which the reservoir emptiesFootnote 1 fully, or a “saturation” form, in which the trigger occurs at a specific threshold. In the former case the interval before a flare correlates with its magnitude; in the latter case the interval after the flare shows the correlation. Figure 1 sketches these possibilities.

Figure 1
figure 1

Top, model timeseries for the “reset” (left) and “saturation” (right) forms of a BUR process for random events in a power-law magnitude distribution as found for flares (e.g. Wheatland, 2000b). The lower panels show the different interval-size correlations for these before and after cases. From Hudson (2020).

Full size image

In the solar case there has been a long history of searches for empirical evidence of a BUR scheme at work. In particular, the “flare build-up study” activity, with its initial meeting in 1975 (Svestka et al., 1976) eventually did not succeed in this respect (Gaizauskas and Švestka, 1987). More recently Wheatland (2000a) explicitly searched for an interval-size relationship, again to no avail. The elusiveness of such a relationship, in view of the apparent necessity for a BUR process in flare/CME occurrence, suggests that some important global property of coronal dynamics remains to be discovered.

Recently Hudson (2020) presented evidence for a solar BUR relationship, but based only on the examination of two unusual active regions (ARs): NOAA 7978 in 1997 and NOAA 10930 in 2006, the “last best” major active regions of Solar Cycles 22 and 23, respectively. That search relied upon GOES soft X-ray peak fluxes in the standard 1-8 Å band, and this study continues that approach. Note that this readily available datum serves as a proxy here for the total radiated energy. Unfortunately the GOES peak flux only represents a tiny fraction (≈1%) of the total radiated energy (Shimizu, 1995). Accordingly any correlation detected will incorporate variance due not only to the uncertainty of the measurement, but also to its interpretation. Both of the regions studied previously appeared at the very ends of their sunspot cycles. This paper attempts to confirm this basic result and to test its generality, based on a larger sample of 14 major active regions in Cycle 24.

2 Data

To test for the generality of the Hudson (2020) result, this article describes the search for interval-size relationships in the major sunspot groups in the recent Cycle 24, 2008-2018. The selection took all groups whose peak sunspot area exceeded 1,000 MSH at some point during their lifetime on the visible hemisphere, numbering 14 in allFootnote 2. Figure 2 shows their daily sunspot areas as given by NOAA, and tabulated in Table 1. Note that for all regions, as expected, the selected regions predominate, and that NOAA 12403, in particular, was almost fully isolated in this sense. The three regions distinguished by dash-dotted lines are, in decreasing order of peak area, AR 12192, AR 12403 (the most isolated), and AR 12673 (a “last best” region of Cycle 24).

Figure 2
figure 2

The day-by-day variation of reported sunspot group areas for the 14 regions selected. AR 12192 (October 2014, at the top) had the largest areas, and AR 12673 (September 2017, at the bottom) had the most powerful flare (SOL2017-09-06). The middle dash-dotted-line region is AR 12403, the region with the least apparent conflict in its magnetic environment in terms of competing flaring active regions (Table 3).

Full size image
Table 1 Active regions: Time spans (indicated as year-month-day-time) and flare occurrences
Full size table

Figure 3 shows the flare/CME event selection, based here upon location as obtained from the Heliophysics Events Knowledgebase (HEK) database (Hurlburt et al., 2012; Martens et al., 2012); this finds locations for GOES 1-8 Å M- and X-class soft X-ray event times via difference-imaging the corresponding EUV images. Note that associating a flare with a given active region requires screening against all three coordinates (including time). To check this screening we fitted the rotational motion of each active region and required flare occurrence to fall within 10 solar degrees in heliolongitude, and a variable range (\(> 4\) degrees) in heliolatitude.

Figure 3
figure 3

Three examples (as listed for Figure 2 of the event selection, showing the heliographic coordinates of flares in competing active regions during the target region time frame. Symbol sizes scale with the logarithm of the peak GOES flux; circles show flares from the selected region, x’s those from other regions.

Full size image

We initially do global correlations across the entire population of flares in each active region, as listed in Table 2, characterizing the correlation as a linear fit of the magnitude-interval scatter plot in log–log space, i.e. the values of the power-law index \(\gamma \) for \(P \propto \Delta t^{\gamma }\), where \(P\) is the GOES peak flux. The table also shows the Pearson correlation coefficients \(r\) and the number of samples (M and X flares). This provides one measure of significance, and the power-law fits to the points provides another. Three exceptional cases appear, as highlighted in boldface in the table. AR 12673 shows a positive correlation in the saturation sense, but below the \(3 \sigma \) level; the strongest positive correlation in the reset case (AR 12371) is not significant. The well-known major region AR 12192 also shows a saturation property, but again below the \(3\sigma \) level. Interestingly a \(2.3\sigma \) negative correlation shows up in AR 11654 for the “reset” case; this result is non-physical in that the toy models cannot predict it. We conclude from these global correlations that there are hints of a preference for the saturation over the reset form of BUR, but that weak correlations and fit errors render these correlations insignificant. Section 3.2 has further discussion of the exceptional cases.

Table 2 Pearson correlation coefficient \(r\) and power-law fit indices for \(P \propto (\Delta t)^{\gamma }\) in terms of both saturation (\(\Delta t\) after a given event) and reset (\(\Delta t\) before a given event) interval-magnitude relationship
Full size table

The results in Table 2 almost uniformly fail to reveal any significant correlations, excepting the regions discussed in Section 3.2 below. The strongest cases for BUR saturation, in either sense, do not attain a 3\(\sigma \) level by either test. The negative correlations (all insignificant) are in any case non-physical in terms of the two toy models, but are included because they reflect the actual properties of the data.

Our earlier result suggested an intermittent appearance of the saturation correlation, based on one-day accumulations of flares from the specific active regions. This ad hoc choice was motivated by the idea that the “saturation” ordering might not persist as the target region evolved over longer periods. We have systematically examined similar one-day integrations in each region, at half-day steps across the time range listed in Table 1. This sampling typically yielded about 10 flares per one-day interval. In these checks no systematic pattern occurred, in disagreement with the earlier results on two isolated regions studied previously in this way (Hudson, 2020).

3 Discussion

3.1 General

As implied by the sketches in Figure 1, a correlation between flare magnitude and waiting time might have two possible realizations, either of which would correspond to a BUR process. A “reset” behavior, in which some parameter such as free energy induces an instability that then discharges to a zero state, has never seemed likely because of the clear evidence for continuing stress in the coronal magnetic field even following a major flare (Wang et al., 1994). The other alternative (“saturation”) behavior envisions a slowly-varying upper limit to a stress parameter, leading to a discharge that can then recur. In either scenario a random Poisson occurrence must dictate the actual times of flare occurrence (Wheatland, 2000b), but the two alternatives respectively predict that the flare magnitudes would correlate with intervals before or after the event, respectively.

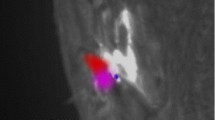
Searches for either pattern (Wheatland, 2000a) had previously reported null results, but Hudson (2020) recently suggested positive results for the “saturation” process in two isolated active regions. Interestingly, these regions appeared at the very ends of their respective Solar Cycles 23 and 24 and were well isolated from other centers of activity. As described in the next section, AR 12673 also was a “last best” region (Hudson et al., 1998) in this sense, but was not isolated. Table 3 provides some information about the environments of the active regions studied here, via a snapshot of activity in other regions present at the time of central meridian passage (CMP) for the target region. None of the targets had zero competition in the sense that other regions were present in all cases, as listed in column 5, with their net areas in column 6 for epochs near central-meridian passage. Of the studied regions, NOAA 12403 was the least conflicted, in the sense of having other regions simultaneously present on the disk, and interestingly the “last best” AR 12673 region was not isolated at all; the snapshots in Figure 4 show that the comparably large region AR 12674 was nearby both in location and in time, peaking in area only a few days before AR 12673,

Figure 4
figure 4

Regions 12673 (the target region) and 12674 (a nearby competing region) at two times, CMP for AR 12673 (left) and on the date of the flare SOL2017-09-06 (right); these are file magnetograms from HMI. The target region NOAA 12673 appears at the lower right (SE quadrant) of the right-hand magnetogram.

Full size image
Table 3 Region complexity: One-day snapshots at CMP for target and other regions
Full size table

3.2 Specific Regions

Only three of the 13 regions examined showed even weak evidence for an interval-magnitude relationship, namely NOAA 12192 and NOAA 12673 (saturation) and NOAA 11654 (reset, but a negative and therefore non-physical correlation). These entries are bold-faced in Table 2. None reach 3\(\sigma \) significance for either sense of BUR, by the two criteria considered. Of these, the “last best” region NOAA 12673 had the smallest area of all, barely exceeding 1000 MSH on one day (comparison shown in Figure 2). Nevertheless this region produced both the most energetic flare of Cycle 24, namely SOL2017-09-06 (X9.3), plus the spectacular limb event SOL2017-09-10 (X8.2). Figure 5 shows the two senses of correlation of soft X-ray peak power in 1–8Å vs. the waiting times for flares covering SOL2017-09-03T09:26 through SOL2017-09-09T06:56. The saturation ordering of the data shows more organization than the reset ordering, but the correlation is not strong. The Pearson correlation coefficient also suggests only weak significance, \(r = 0.17\) for 71 degrees of freedom, P = 85%, with the power-law \(\gamma = 0.50 \pm 0.18\) for the full data interval. As an additional check of significance, the linear fit for the log–log points for the “saturation” ordering (left panel) has slope value \(\gamma = 0.50 \pm 0.18\) for the forward case (\(P \propto \Delta t^{\gamma }\)) and \(\gamma = 0.21\pm 0.07\) with variables reversed. This time range does not extend to the time of the limb flare SOL2017-09-10 because of the incompleteness of the database close to the W limb. Note that the detected correlation depends upon flares with GOES classes M and X, which minimizes any systematic effect due to the obscuration of weaker events following brighter ones (Wheatland, 2001; Hudson, Fletcher, and McTiernan, 2014). This would in any case result in longer intervals, rather than shorter ones.

Figure 5
figure 5

Interval-magnitude correlation plots for AR 12673: the “saturation” (left) and “reset” case (right), for events in the time range of SOL2017-09-03T09:26 through SOL2017-09-09T06:56.

Full size image

The behavior here differs from that found by Hudson (2020) in at least two ways. First, NOAA 12673 was distinctly not an isolated group, suggesting that the coronal environment of this region has not masked its BUR behavior. The correlation appears in a long (six-day) integration, whereas in the previous study it appeared intermittently and not in long integrations. This suggests that any hypothetical saturation level defining successive flares, as implied by the “saturation” form of BUR, somehow does not vary greatly over the full six-day span.

4 Conclusions

The results presented here extend the search for evidence of a build-up/release pattern of flare/CME behavior, commonly regarded as an essential attribute of flare statistics, but to the author’s knowledge something that has never previously been confirmed empirically. The new search of GOES flare statistics for the largest sunspot groups of Cycle 24 has not revealed the existence of a correlation between flare magnitude and the waiting time until the next flare, thought to reveal a mechanism in which a reservoir (containing free magnetic energy, for example) releases random amounts of its content at a prescribed threshold level. This contradicts the earlier finding (Hudson, 2020) of such a correlation, apparently present in two isolated regions. The weakness and intermittency of any such correlation means that it has no application to the prediction of flare properties, unlike the case of the pulsar PSR J0537-6910, for which Middleditch et al. (2006) found a precise predictive capability.

How can we reconcile the negative results here with the commonly accepted picture of magnetic energy storage and release? For weak events it seems natural to turn to a “sandpile” model (Lu and Hamilton, 1991), in which the reservoir has great depth and is unaffected by event occurrence, by design. Such a “nonstationary avalanche model” is consistent with the waiting-time distributions of GOES events (Wheatland, 2000b). But the energy of a major solar flare/CME event may involve a large fraction of the available energy (e.g. Hudson, 2011). In the well-studied case of SOL2011-02-15, Sun et al. (2012) compared the flare total energy with the estimated free energy as inferred from an extrapolation of the magnetic field. As shown in their Fig. 4, the flare consumed of order 1/4 of the total available (free) magnetic energy. Such a finding might not agree with a scale-invariant avalanche model, because it implies a major perturbation of the reservoir and conflicts with the model assumption of a time-stationary “sandpile.” Indeed, both observation (Wang et al., 1994) and theory (Melrose, 1995) require that some free energy must remain in the corona even after a major event.

Despite the negative findings in this study, the importance of this topic suggests that further investigations should proceed, perhaps using better proxies than the GOES peak fluxes.