A Model of a Tidally Synchronized Solar Dynamo

Abstract

We discuss a solar dynamo model of Tayler–Spruit type whose $\Omega$-effect is conventionally produced by a solar-like differential rotation but whose $\alpha$-effect is assumed to be periodically modulated by planetary tidal forcing. This resonance-like effect has its rationale in the tendency of the current-driven Tayler instability to undergo intrinsic helicity oscillations which, in turn, can be synchronized by periodic tidal perturbations. Specifically, we focus on the 11.07-years alignment periodicity of the tidally dominant planets Venus, Earth, and Jupiter, whose persistent synchronization with the solar dynamo is briefly touched upon. The typically emerging dynamo modes are dipolar fields, oscillating with a 22.14-years period or pulsating with a 11.07-years period, but also quadrupolar fields with corresponding periodicities. In the absence of any constant part of $\alpha$, we prove the sub-critical nature of this Tayler–Spruit type dynamo. The resulting amplitude of the $\alpha$ oscillation that is required for dynamo action turns out to lie in the order of $1~\mbox{m}\,\mbox{s}^{-1}$, which seems not implausible for the Sun. When starting with a more classical, non-periodic part of $\alpha$, even less of the oscillatory $\alpha$ part is needed to synchronize the entire dynamo. Typically, the dipole solutions show butterfly diagrams, although their shapes are not convincing yet. Phase coherent transitions between dipoles and quadrupoles, which are reminiscent of the observed behavior during the Maunder minimum, can easily be triggered by long-term variations of dynamo parameters, but may also occur spontaneously even for fixed parameters. Further interesting features of the model are the typical second intensity peak and the intermittent appearance of reversed helicities in both hemispheres.

Appendix

In this appendix, we validate our numerical model by considering again the model of Jennings and Weiss (1991) which includes a (not very physical) quenching of the $\Omega$-effect by the back-reaction of the magnetic field in the specific form

$$\begin{aligned} \omega (\theta ,t) =&\omega _{0} \sin (\theta )/ \bigl(1+q_{\omega } B^{2}( \theta ,t)\bigr), \end{aligned}$$

(9)

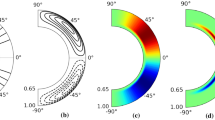
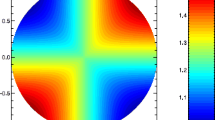
while leaving the $\alpha$-effect unaffected. Fixing $\alpha _{0}=-1$ and the quenching parameter $q_{\omega }=1$, Figure 17 shows the arising spatio-temporal dynamo behavior for two different values $\omega _{0}=170$ (a), (b), (c) and $\omega _{0}=250$ (d), (e), (f). The first row (a), (d) shows $B(\theta ,t)$, the second row shows $A(\theta ,t)$, and the third row shows $\omega (\theta ,t)$ (we skip $\alpha (\theta )= \alpha _{0} \cos (\theta )$ because it is time-independent). Interestingly, depending on the value of $\omega _{0}$, the system develops a butterfly diagram pointing either away from (a) or towards (d) the equator. In either case, the direction follows basically the isolines of $\omega$; see (c) and (f), according to a theorem by Yoshimura (1975).

Figure 17

Spatio-temporal behavior of a simple $\alpha$–$\Omega$ model with pure $\Omega$-quenching, for two different intensities of the differential rotation, $\omega _{0}=170$ (a) – (c), and $\omega _{0}=250$ (d) – (f). The upper two panels (a), (d) show $B(\theta ,t)$, the central two panels (b), (e) show $A(\theta ,t)$, the lower two panels (c), (f) show $\omega (\theta ,t)$. Note the “wrong” butterfly direction for $\omega _{0}=170$ (a), and the correct direction for $\omega _{0}=250$ (d). In either case, the toroidal flux (a), (d) is mainly transported along the isolines of $\omega (\theta ,t)$ (see (c), (f)), according to Yoshimura’s rule.