Wage Inequality and Structural Change

Abstract

Income inequality in the context of large structural change has received a lot of attention in the literature, but most studies relied on household post-transfer inequality measures. This study utilizes a novel and fairly comprehensive collection of micro data sets from between 1980’s and 2010 for both advanced market economies and economies undergoing transition from central planning to market based system. We show that wage inequality was initially lower in transition economies and immediately upon the change of the economic system surpassed the levels observed in advanced economies. We find a very weak link between structural change and wages in both advanced and post-transition economies, despite the predictions from skill-biased technological change literature. The decomposition of changes in wage inequality into a part attributable to changes in characteristics (mainly education) and a part attributable to changes in rewards does not yield any leading factors.

1 Introduction

There is a number of theoretical reasons why a structural shock may matter for the relationship between wage compression and normatively understood inequality. Shocks usually occur with adjustment frictions, which typically imply a larger role for the unexplained component (adjustment in characteristics of the labor force takes longer time than adjustment in rewards to these characteristics). In the context of a Mincerian wage regression ($w = \beta X + \epsilon$) changes in $\beta$ will drive changes of w, given roughly stable X. Accordingly, changes in wage dispersion will signify changes in inequality, until quantities fully adjust. Moreover, since eventually shocks trigger adjustment in X, the question is if immediate reaction in $\beta$ drives the incentives for these adjustments in a way that restores initial compression or leads to a reshuffling of the social structures.

Importantly, the earnings (de)compression and the household income (in)equality need not be directly related. The difference between the two is not only statistical (gross for an individual vs. net of taxes and subsidies for a household) but also conceptual. Namely, with high dispersion of individual characteristics, one would expect low compression of wages which need not imply inequality in the normative understanding of the term (Salverda and Checchi 2014). Consider a frictionless wage process $w=X\beta +\epsilon$, where the random noise to wage process ($\epsilon \sim i.i.d$) is negligible and there are no biases/constraints in choosing the relevant characteristics X. Under such setting, any dispersion in X will be reflected in the dispersion of wages, but this dispersion need not reflect normatively understood inequality, since there are no constraints on the choice is X. Naturally, $\beta$ may amplify or mitigate the dispersion of wages, conditional on X, but given $\beta$, change in labor structure automatically translates to a change in the wage distribution. However, if a process is characterized by a large $\epsilon$ component or if there are constraints on which X individuals may possess, then for a given dispersion of X, wage dispersion would be amplified relative to characteristics.

Compelling evidence shows that structural shocks triggered an increase of income inequality (Milanovic 1998). However, the typical indicators of income inequality measure post-redistribution household income inequality rather than wage inequality. Note, that changes in post-redistribution total household income inequality are much more complex from a theoretical perspective than wage inequality: they may additionally involve tax policy, transfer policy, returns to wealth, household joint strategies on labor supply decisions, etc. None of these factors needs to be associated with a structural change per se, whereas changes in wage inequality remain intimately related to the process of structural change. This paper attempts to fill the gap in the literature on wage compression and structural change analyzing the case of transition from centrally planned to market economy.

Indeed, replacing central planning with a market based system created room for unprecedented and rapid wage decompression in the Central and Eastern Europe (CEE, see e.g.Milanovic 1999; Brainerd 2000). Highly centralized wage-setting mechanisms were replaced by market mechanisms, while high inflation along with large shocks to employment levels and employment structure along with high churning made it essentially impossible to “preserve”wages from either a firm-level or an individual-level perspective.

Transition from a centrally planned to a market economy, as experienced by Central and Eastern European (CEE) countries, constitutes an interesting case study for, at least, two reasons. First, the region comprises a relatively large set of dispersed economies, while these countries have also followed somewhat different policies, also in terms of labor market equality. Suffice it to say that, in spite of being a single country prior to 1992, Czech Republic has one of the lowest and Slovak Republic one of the highest unemployment rates in Europe. Second, the transition started nearly three decades ago, which yields a sufficiently long period to observe the wage compression processes. However, due to limitations in data availability, there was little comparative research so far into wage (de)compression in the course of a large structural shock. In most transition economies, household surveys do not permit direct identification of wages by person, while not all labor force surveys collect information on wages. Also, one needs a sufficiently long horizon. For example, Gernandt and Pfeiffer (2009) analyze wage convergence between East and West Germany showing that even after 15 years, wages of workers in East and West Germany are still different.¹ Milanovic (1999), Milanovic and Ersado (2012) analyze household survey data and provide evidence that increase in inequality stems mostly from disappearing middle of the wage distribution.² By contrast, Pryor (2014) argues that despite transition, around the year 2000 CEE countries are characterized by lesser income inequality than would have been expected given their economic development. One of the reasons behind this result may be the institutional inertia. Indeed, institutional setting seems to matter for wage compression, as shown in a recent comprehensive comparative study by Salverda and Checchi (2014). Building on earlier insights by Bertola et al. (2001) they argue that what matters most for the inequality is the wage compression “from below”.³ Unfortunately, both Pryor (2014) and Salverda and Checchi (2014) analyze data from a decade or two past the transition, they pay only a lip service to the structural change from a centrally planned to a market economy.

In this study we utilize a large and novel collection of micro-economic data from as many as 31 countries of which 14 are transition economies. Our earliest samples come from 1984 and in some cases coverage continues to 2014, with over 42 million individuals observed. These data sets have been harmonized for conforming definitions of variables.⁴ Hence, for each country we are able to produce comparable measures of wage distribution as well as provide a variety of counterfactual exercises.

Given the main interests of the earlier literature as well as policy relevance, we formulate the following three research objectives. First, we provide a description of the trends in the wage compression across time in the process of transition from a centrally planned to a market economy. We utilize the data from non-transition countries to provide a baseline scenario, as every country experienced skill-biased technological change and globalization over this horizon. Our findings show that the initial shock to wage distribution was essentially instantaneous, whereas countries experiencing a rapid structural change effectively do not return to the initial levels of wage compression.

Second, we provide a series of counterfactual analyses, which help to understand whether changes in wage distribution reflect adjustment in prices ($\beta$’s) or in quantities (X’s). Namely, earlier literature seems to suggest that economic processes affect the returns to individual characteristics and thus influence the wage distribution. However, an important feature in all transition economies has been an increase in tertiary enrollment as well as massive reallocation of the labor force coupled with relatively high unemployment in some of these countries. We construct counterfactual distributions of wages to assess how much of the change in the wage structure occurred due to change in labor force structure as opposed to the changing evaluation of the individual characteristics in the course of transition. Given its strong foundation in the economic theory, we pay particular attention to the skill biased technological change. We show that most of the decompression stems from diverging wages, because the labor force remains substantially more homogeneous in terms of productive characteristics than in the advanced market economies.

Third, we provide an analysis of the link between wage inequality and structural changes. The earlier literature argues that the role of the institutional framework is decisive for determining wage compression, particularly “from below”. Given the richness of our data, we are able to develop a series of counterfactual scenarios to assess the role of human capital in the course of a large structural shock. While these estimates do not aspire to be causal in terms of the relationship between a given institution and a level of wage compression, they are informative about the effects of shocks— such as transition—on the distribution of wages given the institutional design. We show that more structural change is actually associated with lower extent of wage decompression.

Our study is structured as follows. In the next section we provide an overview of the existing literature, showing how our paper contributes to the body of earlier research. We also discuss how wage compression is measured in the literature so far. Given the diversity of data sources and its heterogeneity, we discuss at large the characteristics of the acquired datasets and limits to their usefulness from the perspective of our main research question in Sect. 4. The methodology for constructing the counterfactual distributions is discussed in Sect. 4.2, whereas the estimates for the original data and the counterfactual scenarios are presented in Sect. 5. In concluding remarks we emphasize the policy implications of our study along with directions for future research.

2 Literature Review

Analyzing the case of the US over 1980s and 1990s DiNardo and Card (2002) provide a list of possible explanations for changes in wage distribution. In addition to the usual suspect of the skill-biased technical change (SBTC) they also point to gender gaps, racial gaps and cohort gaps within educational groups.⁵ SBTC hypothesis postulates that the demand for “more-skilled”workers combined with the relative abundance of skilled workers determine jointly the dynamics of the wages disaggregated by educational groups increasing the dispersion between high earners and low earners due to technology-skill complementarities. Indeed, as shown by Autor et al. (2008), there have been substantial price adjustments in the bottom of the earnings distribution in the US, but their effect on total wage inequality has been moderated (or effectively wiped out) by the upward quantitative adjustment for workers with low earnings.

While the role of SBTC seems to have been corroborated empirically, the trends in gender, racial and other gaps are less systematic. For example, in the US the gender wage gaps appear to drop (Blau and Kahn 2016), but this trend is not universal (Polachek and Xiang 2014; Rendall 2013). Racial gaps tend to be remarkably stable in the US (Heywood and Parent 2012; Kreisman and Rangel 2015) and other countries (Longhi et al. 2012; Lang et al. 2012). College premium have first exhibited a stark increase (Grogger and Eide 1995; Dinardo et al. 1996), but in many countries it was followed by a substantial decline (Walker and Zhu 2008; Acemoglu and Autor 2011) with increasing dispersion of returns to higher education (Reimer et al. 2008; Green and Zhu 2010). Overall, in advanced economies, changes in the wage distribution do not follow one single pattern, with multiple processes interacting (Checchi et al. 2016).

There are also natural limitations to this strand of the literature. First, since SBTC and equalization of opportunities are slow moving processes, analyzing the effects of these structural changes on wage compression is very data intensive both in terms of length of comparable micro-level data and in terms of data quality. Short periods of observation make it impossible to notice substantial changes in wage distribution, and only few countries can offer comparable micro-level datasets for a few decades. Second, it is also relatively rare in most countries that wage data is systematically collected in labor force surveys (or analogous studies). Hence, most of the analyses concern few countries for which data is readily available: the US (e.g. Lee 1999; Acemoglu and Autor 2011), Canada (Lemieux 2006), Japan (Kawaguchi and Mori 2008) and Germany (Beaudry and Green 2003; Dustmann et al. 2009).

Given these high data requirements, substantially less research analyzed changes of wage distribution in countries undergoing a sudden structural change of replacing centrally planned with a market based system. This rather unique case of shock to the economic system involved both types of processes expected to drive SBTC: opening of the transition economies to global trade and immediate installation of direct price incentives where there were substantially compressed direct rewards to individual skills and characteristics. This process is modeled in a general equilibrium simulation framework by Aghion and Commander (1999), who show that indeed technological and organizational change may drive wage decompression if asymmetrically affected groups cannot smoothly adjust their skills. However, in their setup, majority of the effect comes from differentiated employment opportunities for various groups and not directly from changing distribution of wages for the respective groups. This stylized framework is useful for interpreting the empirical findings in the (scarce) literature. For example, Milanovic (1999) argues that the decompression of wages stems from dismantling of the state sector with compressed wage structure, and its replacement by the newly-emerging private sector with much broader wage distribution. Similar insights stem from study by Keane and Prasad (2006), who argue that the reallocation of workers from the state owned sector to private sector translated to replacing a compressed distribution of wages with a more dispersed one.

These micro-level studies were complemented by multiple cross-country comparisons utilizing more or less standardized measures of income inequality (e.g. Milanovic and Ersado 2012; Aristei and Perugini 2012, 2014), and which mostly focus on household income inequality rather than earnings dispersion. Gernandt and Pfeiffer (2009) rely on data from Germany and analyze the convergence between the average in the East and the West. However, this study does not address the dispersion of wages inside the two regions. Unfortunately, majority of other empirical studies focuses on issues such as poverty incidence and utilizes household after-transfer income inequality rather than earnings dispersion (Ott and Wagner 2013, provide an overview of earlier literature in the field).

The literature referring to the sudden structural change of transition so far failed to address a number of issues relevant for the literature on structural change and wage compression.⁶ First, studies tend to attribute increased income inequality to increased earnings dispersion due to the flow of workers from state owned firms to the emerging private sector with more decompressed wage distribution. However, recent studies show that there was in fact little reallocation of workers per se, rather premature exits to retirement and entry of young cohorts drove the overall change in employment structure (Tyrowicz and van der Velde 2018). There is also substantial evidence that privatizations rather than worker flows explain the change in ownership structure of employment. Hence, although there has possibly been different wage dispersion patterns between the emerging private sector and the state owned sector, the actual flows of workers appear to have been smaller than initially expected. Moreover, these studies do not explain why the wage distribution in the private sector should be more dispersed—in other words, due to which processes and how much more dispersed should one expect it to be.

Second, there has been little insights into the role played by the changing composition of the labor force in changing the distribution of wages. Namely, well documented phenomenon, such as the increase in tertiary enrollment, growth in service sector employment and relatively fast aging of the population all may contribute to changing the dispersion of wages, even if returns to individual characteristics do not change. Analyses of the SBTC and wage compression show that ‘prices’ matter substantially for the changes in the distributions of wages, because they react to the changes in the (relative) abundance of demanded skills. However, with SBTC, because all these changes are gradual, there can be adjustments in both prices and quantities. With changes as sharp as transition from a centrally planned to a market economy one should expect prices to play a bigger role in changing wage distribution, at least in the short and medium run. These are the issues our analysis will help to address.

3 Measuring Wage Inequality

Literature provides several concepts to describe wage distribution. Salverda and Checchi (2014) highlight conceptual difference between dispersion and inequality. In their view, dispersion is just a mathematical difference, which does not have to be always an inequality—e.g. dispersion does not have to include differences in efforts or characteristics. From a definitional perspective, dispersion measures are typically position-dependent measures, i.e. capturing the distance between given percentiles of the distribution, whereas the inequality literature typically relies on synthetic indicators about the shape of the distributions, such as Theil index, Gini index or mean log deviation for example. In this section, we provide information on wage inequality and wage compression measures, and thus justify the use of position-dependent measures as preferred indicators in our study.

Due to a wider availability of micro-level wage or income data, empirical literature on inequality has frequently relied on synthetic indicators, such as Gini or Theil index as well as measures based on distribution moments (e.g. coefficient of variation, mean log deviation, standard deviation of logs, etc. Card et al. 2004; Töngür and Elveren 2014; Checchi et al. 2016). Mathematical structure of these measures allows to fulfill basic properties such as mean independence, size independence, symmetry, transfer sensitivity as well as decomposability (Shorrocks 1980). Gini satisfies the first four, but not the last of these five properties, whereas most generalized entropy measures satisfy them all (e.g. mean log deviation, Theil index). Despite this, Gini coefficient is the most popular in inequality research, possibly due to its intuitive character and interpretation.

Still there are some drawbacks of using synthetic measures. First, none of them has theoretical confidence intervals, so the only feasible alternative is bootstrapping. Second, most of the studies rely on survey data and thus are bounded with survey error if they are to be treated as approximation for the entire underlying population. Third and most important, these indicators exhibit the same dynamics no matter whether the compression of wages changes from below or from above. Hence, while these indicators are intuitive for discussion of inequality, they are less informative from the perspective of the research question in this study.

Literature also formulated measures dedicated to poverty and exclusion, such as low pay incidence (Meulders et al. 2004), in-work poverty (Bennett 2014), share of income accruing to the top 1%, etc. We abstract from these measures in the reminder of this paper due to definitional issues: poverty lines definitions differ across countries and usually refer to household level, whereas top 1% share of income cannot be adequately measured in survey data as these are often censored. It is well documented that top earners are weakly represented in surveys studies, such as the majority of data sources utilized here. Also, structure of earnings survey do not report the earnings of individuals below the legal limits such as minimum wage (that would be self-incrimination in many legal systems, which firms naturally attempt to avoid even if they violate the minimum wage regulations). In sum, some sources of data particularly poorly capture high earners, whereas others particularly poorly capture low earners. Hence, focusing only on the wages from the top or the bottom of the distribution may be relatively more biased than measures based on ranges between wages.

Given the nature of the analyzed processes—large structural change and skill biased technological change—one would expect the patterns to differ between the rich, the poor and middle class workers. Considering such research question and knowing the strength and weaknesses of inequality and compression/dispersion measures, we decided to focus on changes in positional measures. Rather than choosing one specific measure, we analyze several most frequently used measures as indicators of changes in the wage compression: log difference between the 90th, the 50th and the 10th percentiles, as well as the difference between 75th and the 25th percentiles (e.g. Blau and Kahn 1996b; Koeniger et al. 2007; Koeniger and Leonardi 2007; Autor et al. 2008). The popularity of the mentioned measures of wage compression is well reasoned. First, 90th and 10th percentiles combined with the median allow to distinguish within the whole distribution the dispersion from above and the dispersion from below. Both are likely to be driven by other processes, not necessarily occurring under the same circumstances (see also Beaudry and Green 2003; Milanovic and Ersado 2012). Measures focused on quartiles of the distribution capture the non-extreme majority of the labor market and thus complement the picture. To compare dynamics of changes in wage distribution, we also include in our analysis the most popular representatives of the synthetic measures—the Gini index and the mean log deviation⁷.

4 Data and Empirical Strategy

In this section, we describe the data collected and the empirical strategy followed. First, we describe data sources used to build a novel, coherent international and multiannual database employed in this study. Then we show how the wide array of micro-data sets was used to compute measures of wage dispersion comparative across time and between countries. We also show how our measures fare against the widely accessible indicators from OECD Statistics. Finally, we show the main advantage of using the microeconomic data, i.e. we describe the counterfactual scenarios.

4.1 Data

In order to address the question at hand we collected a large number of micro-level data sets. Already in 1990s, International Social Survey Program (ISSP) made individual data on wages available for some selected countries (see Blau and Kahn 1992, 2003; Polachek and Xiang 2014). However, ISSP often changes the way wage data is collected between nominal and categorical, which makes it rare that data for a given country could be analyzed continuously over time. Montenegro and Hirn (2009) develop The World Bank micro-database with data from 120 countries, in total app. 600 surveys (utilized by Nopo et al. 2012; Rendall 2013; Gindling et al. 2016 among others).⁸ However, the focus of The World Bank is on the most recent years and on developing countries, which results in relatively poorer coverage of 1980s and 1990s as well as Europe. Luxembourg Income Study operates an initiative to standardize data from European countries, LISSY (utilized by Polachek and Xiang 2014; Pryor 2014 among others). However, LISSY comprises mostly data from European Household Community Panel and EU Survey of Income and Living Conditions (EU-SILC). ECHP covers EU member states from 1994, with poor coverage of CEECs. In the latter coverage of CEECs starts usually in late 1990s. Moreover, for many countries and years EU-SILC collects detailed data on annual salaries, but not on hours and months worked. Hence, meaningful comparisons are only possible between full-time full-year salaried workers.

Given these constraints, we created a novel collection of individual-level datasets from transition countries. We addressed all statistical offices in CEE region and acquired labor force surveys (LFS) and household budget surveys (HBS) data. We asked for data from as early as they are available, which is typically 1993–1995 for most CEECs. Data for benchmark countries were acquired from the standardized EU data sources such as ECHP and EU-SILC as well as Structure of Earnings Survey (SES), provided by the Eurostat. In the case of Hungary and Poland we also acquired SES data from statistical offices, which gave us access to a larger number of years for these countries. In addition, for two large transition countries—Ukraine and Russia—we utilize a dedicated large-scale representative panel data: Ukrainian Labor Market Survey and Russian Labor Market Survey.

Compared to these earlier efforts, our database is rich and comprehensive. We can track labor markets of 31 countries (of which 14 are post-transition economies) between 1984 and 2014. The data sources are discussed in Appendix 1 and country coverage is summarized in the Table 2. While the number of countries covered is lower than in The World Bank study, regional coverage of the transition economies is more comprehensive (14 countries in our database vs. 7 in the World Bank analysis). Also our coverage of 1990s is richer than in earlier literature. For example, compared to Milanovic (1999) we have weaker coverage of the pre-transition years, but we are able to comprise many transition economies from 1992/1993 onwards.

In total, we collected information on over 40 million individuals. A data set was included in our study if it contained information on individual wages, hours worked, education, age, gender and occupation. As data for each country (and often each source) have differentiated variable definitions, we harmonize all variables to identify the same concepts. Wages are expressed in local currency units, in net value (the only exception is SES, where wages are given in gross terms). For the definition of hours we use the answer to a question about “hours typically worked” or “hours normally worked”. If a survey did not ask about either of the two, the hours variable was not constructed and sample was not used in hourly wage analyses. If a given dataset contained data on monthly wage and weekly hours, we recoded wages to reflect hourly compensation, assuming four weeks per month. Since hours are not available in each dataset, we also utilize average monthly wages for full time workers.

Similar steps were taken to harmonize education, age, gender and occupation variables. This harmonization of data is typically not controversial, but it did narrow the number of categories to be considered for each variable. For example, in the case of education, after comparing all the sources, the only possible consistent definition comprises three levels: primary or below, secondary and tertiary or above. As in some sources age has been aggregated in age groups, we follow this classification for all the sources (below 19, 20–29, 30–39, 40–49, 50–59 and 60+). The basic statistics of the harmonized characteristics over time are presented in Fig. 3.

4.2 Measures of Wage Inequality

Using the novel, large, individual-level labor market dataset described above, we calculate indicators of wage compression. All measures are derived for hourly wages, but some datasets do not contain information on hours. Hence, we also develop these indicators for monthly reported wage income and present these results in the “Appendix”. All the indicators are computed in the same manner across all the datasets, which makes them methodologically comparable.

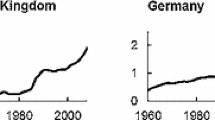
Not all indicators we derive are identical to measures reported in various data sources on income inequality. For example, comparing to the OECD database reveals relatively strong correlation where our selection of countries and OECD data coverage overlaps for the income percentile ratios, but not for Gini, see Fig. 1. This comparison shows how numerous assumptions are taken to compute the OECD indicators and how sometimes they need not reflect the actual wage compression patterns. The highest correlation—app. 50%—is found for the p90/p10 ratio. We also find roughly similar figures for the upper half of the wage distribution. Much lower correlation concerns the bottom half of the wage distribution—correlation between our indicators and those reported by the OECD falls to 24%. The reasons behind this lower correlation stem from the data shortages discussed earlier (e.g. in EU-SILC). Since indicators for the lower half of the wage distribution differ between OECD and our data, one should expect Gini to be an accumulation of these discrepancies, which indeed is the case.

Fig. 1

Source: indicators of inequality based on total monthly wages of full time workers in OECD (http://stats.oecd.org/section:Labour/Earnings), total monthly wages in own measures. Data coverage from OECD is smaller than reported in Table 2. Overall, correlations computed for the following countries: Czechia, Estonia, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Latvia, Lithuania, Luxembourg, Netherlands, Norway, Poland, Portugal, Slovakia, Spain, Sweden. Transition countries coverage in the OECD data starts usually in 2000s. Detailed comparative statistics reported in Table 4 in the “Appendix”

Comparison of the inequality measures derived from micro-datasets and OECD indicators.

However, knowing the methodological choices in constructing the OECD indicators, one should expect exactly these discrepancies. First, OECD only uses wages of full-time employees. Hence, own measures show substantially more dispersion than the OECD data. Second, OECD relies mostly on household level data (such as the EU-SILC for example), which makes it less comparable to studies focusing on labor issues (such as the labor force surveys) and studies focusing on other issues, which also inquire about self-reported wages. For example, measures of wage compression for one selected country— Poland—derived from EU-SILC and from Polish LFS differ substantially, with household level data revealing much lower wage compression at the bottom half of income distribution. On the other hand, some outcomes differ also because the data collection used in this study are sometimes not fully representative surveys. For example, data from the ISSP show systematically higher measures of dispersion. While this data source has been used extensively in labor market research (cfr.Blau and Kahn 1992, 1996b, 2003), one needs to recognize smaller sample size than in representative surveys as well as the fact that in self-administered surveys responders tend to report more rounded numbers when reporting wages.

Overall, the comparison reported in Fig. 1 reveals the advantages of the methodological approach taken in this study. First, unlike studies utilizing wage compression measures compiled by other sources, we may obtain measures which reflect the general population of workers, not a systematically selected subsample (e.g. full-time workers). Second, we may obtain these indicators for years and countries for which standard data sources such as OECD, World Income Inequality Database or Transmonee are short in coverage. Finally, we are specific to utilize worker earned income rather than household income measures. Naturally, not all data sources are characterized by the same reliability of the indicators. To address this issue, all estimations include data source fixed effects. Having discussed data characteristics, in the remainder of this study we pursue with the empirical analysis.

4.3 Obtaining the Counterfactual Distribution of Wages

So far, we were focused only on actual reported wages to measure changes in (hourly) wage inequality. However, change in wages may stem from two distinct processes: structural change of the underlying labor force characteristics (e.g. increase in tertiary attainment) and the change in rewards to these characteristics. To isolate the first effect we provide counterfactual scenarios utilizing estimated structure of rewards from a benchmark dataset. Given the richness of this data, we rely on American Community Survey. For the sake of robustness, we obtain three sets of benchmark rewards: from ACS wave of 1990, wave of 2000 and wave of 2010. Using these estimates we provide counterfactual structures of wages for each micro-data set in our sample, independently. Then, changes across time reflect only changes in labor force structure— not how it is being rewarded. The models to obtain the counterfactual structure of wages are highly saturated, with two-way interactions of education (3 levels), age (5 groups), gender and occupation (9 levels).

The parametric approach to wage structure is appealing, but may be susceptible to several methodological hazards. Thus, we also utilize Dinardo et al. (1996) semi-parametric approach (henceforth, interchangeably DFL). Using ACS data from 1990 wave, we estimate the likelihood function that a given person from a given country and data source in a given year has the same characteristics as an average American worker.

$$\begin{aligned} weight_{i, j} = \frac{1-Pr_{i,j}(ACS = 1 | x)}{Pr_{i,j}(ACS = 1 | x)} \cdot \frac{Pr_{i,j}(ACS = 1)}{1-Pr_{i,j}(ACS = 1)} \end{aligned}$$

(1)

where ACS is equal to 1 if the worker is from the US ACS sample and zero otherwise, x are the characteristics of the worker and conditional probabilities are obtained from probit models. Characteristics used in the probit model are the same as in the case of parametric approach, with models run separately for every analyzed sample. These weights are then used to obtain counterfactual distribution of wages as if a given country and data source had identical employment structure as the US from a given wave. On these semi-parametric counterfactual distributions we also obtain measures of wage compression.

This approach has an additional advantage that it allows to partially account for differentiated selectivity patterns. Similar approach was employed by Campos and Jolliffe (2007). By the means of Dinardo et al. (1996) correction, we replicate the weights in the population as if employment was as likely, given age, gender, education and other relevant characteristics. For majority of the distribution, the two counterfactual distributions are expected to correlate relatively well. However, the parametric approach cannot recover dispersion in the top of the earnings distribution. By contrast, DFL reflects it relatively well. This difference stems from the fact that probably high earned incomes are associated not only with highly rewarded characteristics, but also unusually high compensation for them. Hence, although the parametric model is highly saturated (interactions of all the involved characteristics), this part of compensation must be residual in parametric approach and hence cannot be recovered in fitted wages. DFL, meanwhile, only reweighs distributions to replicate the structure of individual characteristics, but takes wages as given. Hence, what is residual and thus omitted in parametric approach, remains on the distribution in the semi-parametric approach of Dinardo et al. (1996). We portray these considerations using example of one transition and one advanced economy in Fig. 4. This comparison yields two important insights for the interpretations of the counterfactual wage compression measures. First, it appears that especially in the top, counterfactuals from DFL may reflect actual distributions closer than parametric one. Hence, for the p90/p50 ratio one should consider estimates on counterfactuals from DFL as more reliable. Second, the estimates concerning p50/p10 are expected to produce similar outcomes.

The exercise with the counterfactual scenarios reveals that changes in the wage structures had a relatively big importance. When cleared of the rewards effect in parametric approach, the time variation in the indicators of wage compression are substantially larger, but in DFL counterfactual scenario the result is the opposite—especially in the case of p50/p10 ratio, see Table 5. This is especially pronounced in the “from the top” compression. These might suggest that the counterfactual scenarios show slightly different stories on changes in workers characteristic and rewards with DFL taking into account more variation caused by other than time trend effects.

5 Results

The results are reported then in three substantive parts. We start from providing the overview of the time patterns as well as cross-sectional heterogeneity. Then we analyze time trends of wage compression measures based on the counterfactual wage distributions. This way we show the contribution of changes in characteristics of workers (mainly connected to increased educational attainment and occupational structure changes) in wage compression processes. In some cases we find that if wage structure would follow only changes in characteristics, the distribution of wages would change in the opposite direction than observed in the data. Finally, we provide analyses on the relationship between selected specific structural changes and wage compression measures. We pay special attention to, separately, inequity on the top and on the bottom of the distribution. Differences between transition and non-transition countries are highlighted.

5.1 Variation of Wage Compression Across Time: Actual and Counterfactual

In the first step we present the estimators of the year effects from a regression with country and source fixed effects for all four indicators of wage compression. These predictive margins report both the magnitude of the effect and the size of the estimated confidence interval and thus permit fairly reliable comparisons across time. Since we control for time and data source fixed effects, the changing country availability in the sample has as small bearing on the results as possible. For the sake of comparison, there were separate estimations for the transition countries and the benchmark countries. The results are reported in Fig. 2.

Fig. 2

Source: hourly wages from data sources described in Table 2, results for the total (monthly) wages available in Fig. 5 in the “Appendix”. Analogous estimations for Gini coefficient and mean log deviation reported in Fig. 6 in the “Appendix”. Marginal effects of years obtained from regressions of wage compression measures as dependent variable on country, source, year and interaction of year and transition dummies as independent variables. Regressions for the full collection of data sets were hourly wage was coherently defined. Robust standard errors used

Wage compression—time trends.

Even this relatively simple descriptive statistic reveals several important observations. First, the adjustment in wage compression were almost immediate, occurring in the first few years of transition. Second, while wages were substantially more compressed in the upper half of the distribution in the transition economies, this is where the adjustment took place—from levels below the benchmark countries, the indicators of compression jump almost instantaneously to the much higher levels and this initial differential continues for the reminder of the sample. Third, there appears to be a very slow, negative trend indicating more wage compression in both transition and benchmark countries, especially in the years post the global financial crisis. Fourth, beyond this initial jump in the upper half of the wage distribution, there were not much changes in the subsequent 20 years of transition. This last conclusion is potentially puzzling—adjustments such as skill biased technical change, plugging into global value chains, etc.— involve substantial adjustments by firms and henceforth by the workers.

Time variation provides for only a small share of changes in inequality. Table 6 reports the estimates of the level effect between transition countries and the benchmark countries along with the estimates of the time trend. We interact the time trend and transition to observe if there are statistically significant differences between the two groups of countries. The results reveal a level effect of transition countries—from 0.6 for the p90/p10 ratio and 0.2–0.3 for p50/p10 and p90/p50 ratios. These differences are persistent over time, but not very large: with the current rate of change, it would take the transition countries approximately 10 years to close down the gap. Recall Fig. 2, the gap emerged in the first 2–3 years of early transition. There is no catching-up effect when it comes to a top-down inequality (p90/p10).

We complement these estimates with a similar analysis but for the counterfactual distributions, parametric and non-parametric, also reported in Table 6. Using “prices” of individual characteristics from the US, we reestimate the distributions of wages based on individual characteristics in both transition and benchmark countries. First, we find that the counterfactual wage distributions are in fact more compressed in transition countries than in the advanced economies. The negative estimate of the transition dummy is consistent across all indicators of wage compression (sometimes insignificant, but never positive). This means that increase in the dispersion of wages was due to swiftly adjusting prices of individual characteristics rather than characteristics of workers before the introduction of the market economy.

Second, the speed of convergence between the two groups of countries appears much faster, in the parametric counterfactuals and much slower or even inexistent in semi-parametric counterfactuals. Hence, it appears that any divergence between the two groups of countries stems from prices, whereas any convergence between the two groups of countries comes from characteristics of the labor force becoming more similar. Lack of convergence revealed by the DFL counterfactuals suggests that the abnormally high wages received by some individuals, beyond their characteristics, stand behind relatively higher dispersion of wages in transition countries. On the other hand, the top-bottom comparisons (p90/p10 and p90/p50) reveal relatively high convergence, requiring approximately 10 years for the transition countries to catch up with the advanced market economies.

Third, the disparities in wage dispersion between the two groups of countries are particularly pronounced at the bottom half of the wage distribution. This is especially relevant from a policy perspective—most of the transition countries kept the institutional features such as minimum wages and centralized wage bargaining. Despite these institutional arrangements, wage distribution decompressed rapidly and remained as decompressed ever since. Comparison of the parametric and semi-parametric counterfactuals reveals that this process was stronger for the unexplained part of the variation in wages.

5.2 Wage Compression and the Indicators of Structural Change

The analysis of time trends alone is not satisfactory. To address the economics behind the time trends we follow the vast literature on the structural change. We collected several standard indicators: share of trade in GDP (to reflect globalization), share of services in employment (to reflect the transition between industrial and service based society), high-technology share in exports and high-skill share in employment (to reflect the position of an economy in the global value chain). Each of these indicators measures a secular, global trend. However, countries absorb these changes at varied pace. Our objective is to test if, and to which extent, differences in absorbing these global trends explain the variation in wage compression.⁹ We include country (and data source) fixed effects, so mostly the variation over time is exploited. To account for possible differences between the countries undergoing a rapid structural change and countries experiencing it gradually, we provide also estimates of the interaction term for the dummy denoting transition countries. These correlations are computed for original measures of the wage compression and for the counterfactual ones. Following the theoretical insight that the effects of structural change will differ for workers at the bottom and at the top of the wage distribution, we include the positional measures that allow to compare the effects for below median and above median workers. Results are reported in Table 1.

Table 1 Wage compression and the indicators of structural change

The indicators of structural change correlate mostly with the decompression in the lower half of the wage distribution. Most indicators of structural change exhibit negative correlation, which implies that more compressed wage distributions and more structural change coexist, not the vice versa. Since some changes have been more rapid in transition economies, some of the interaction terms provide significant estimates, but usually making the negative correlations larger not weaker. In particular, technology intensity of exports is only significant for the transition countries whereas the compression is twice as strong for the share of R&D expenditures in GDP in transition than in non-transition countries. For the top of the distribution, most correlations become insignificant once we take away the effects of the prices. The only exception is the share of high-skilled workers in the economy, which too is associated with lower wage compression. Hence, these results suggest that structural shocks correlate mostly with changes in prices, but not changes of individual characteristics.

Clearly, correlations discussed above cannot be indicative of causality. Rather, they document that despite controlling for country-level heterogeneity, there seems to be significant correlation between the level of structural change and changes in the wage compression. This correlation is driven predominantly by changing prices.

6 Conclusions

In explaining wage inequality, existing literature has focused on skill-biased technical change (SBTC, e.g. DiNardo and Card 2002; Acemoglu and Autor 2011), related notion of college premium (e.g. Grogger and Eide 1995; Walker and Zhu 2008) as well as unionization (e.g. Gosling and Machin 1995; Hibbs and Locking 1996; Card et al. 2004). The notion of institutional or structural change is crucial in all these strands of the literature in explaining the changes in the wage distribution. However, most of the analyzed countries experienced gradual, slow-moving changes, which makes the identification troublesome. The exceptional event of rapid economic transition from a centrally planned to market economies is a great example of a rapid change, where identification may be clearer. Using a novel, unique collection of micro-datasets on wages in this paper we provide consistent estimates of unconditional and conditional wage distribution to analyze the sources of changes in the wage compression.

We show that indeed wage dispersion increased rapidly in early transition and that adjustment was immediate. Since then a slow, negative trend is visible. While wages were more compressed than in the benchmark group of advanced market economies, the rapid increase made wages persistently more dispersed. This effect lasts despite being driven mostly by adjustment in prices—when the variation in prices is eliminated in the counterfactual scenarios, the wages continue to be more compressed in the transition countries. This implies that despite massive labor reallocation and the unprecedented spike in tertiary enrollment, characteristics of the salaried workers still remain more similar in transition countries than in advanced market economies.

To understand the sources of the observed time trends in wage dispersion, we sought to identify to what extent they may be attributed to globalization or skill-biased technical change. We correlate the measures of wage compression—both raw and counterfactual—on the indicators of globalization and structural change. We find that if anything, these processes correlate with more compressed wage distributions. This result partly disappears when we fix the prices of individual characteristics, which implies that adjustment in prices go in the opposite direction as the adjustments in characteristics, reducing the incentives to invest in skills. In fact, adjustment in prices must outpace on average the adjustment in characteristics. However, these effects are contained to the bottom half of the wage distribution. There is substantially less compelling evidence for the top of the wage distribution that globalization and skill-biased technical change affect the distribution of wages.

Usually in one country setting, earlier studies argue that changing returns to skills influence the observed inequality indicators. This evidence was consistent for the US, but less so for Germany and Japan. Our study is not to argue against these earlier findings. We focus on the alternative measures of wage dispersion to emphasize differences in the ‘from below’ and ‘from above’ inequality. We find that indeed most of the effects occur in the bottom half of the distribution, especially if changes happen rapidly, as was the case of transition economies. However, the initial shock in demand appears to have been relatively swiftly absorbed.

Appendices

Appendix 1: Data Sources and Descriptives

1.1 Labor Force Surveys (LFS)

Many of the LFS samples do not contain information on wages (or information on wages is not disclosed due to national legislative implementation of the statistical secrecy clauses; in some cases wages are reported as deciles, which may be used for some studies, but not in wage compression analyses). Hence, in this study we could utilize the data for Croatia, Poland, Serbia as well as France and the UK.

LFS data are self-reported worker data and contain information individual labor market status. LFS are standardized in terms of sample design and general definitions, but not variables. Coding for education, labor market status, occupation and industry differed and were harmonized (ISCO for occupations, NACE for industries). Hourly wages were calculated based on the self-reported monthly net wage and averaged hours of worked per week. The only exception if LFS Croatia where hours information is missing.

1.2 Household Budget Surveys (HBS)

Many of HBS do not comprise individual incomes, rather household incomes by source. In household with two wage earners, individual earnings may only be attributed if the head of the household is a wage earner. This feature makes the wage data not comparable across countries and years. Given these constraints, we only utilize HBS data where individual earnings are reported (along with individual characteristics). This limits the choice of countries to Belarus and Latvia. Another constraint of HBS is that it often lacks data about hours worked. Hence, we can only utilize monthly earnings. Similar to LFS, HBS data is self-reported, typically in net terms.

1.3 Structure of Earnings Survey (SES)

Employers with more than 9 employees, FTE, participate in this large survey program in most European biennially. This data comprises detailed information on earnings, hours and worker as well as employer characteristics. As of 2002 it is standardized within the EU and the data are distributed by the Eurostat. Some of the countries collected their own SES data and thus we were able to extend the data coverage for Hungary and Poland to 1990s. SES data is typically very detailed, with two digit NACE and four digit ISCO. However, this level of data disaggregation is typically missing in other sources. Hence, we resort to one digit aggregation.

1.4 European Community Household Panel (ECHP) and EU-Study of Income and Living Conditions (EU-SILC)

Developed by the Eurostat, ECHP was a European level analog of the household budget surveys in Member States. In principle it contains high quality data on both household structure and earnings, but some relevant data are missing (e.g. coding for urban/rural residence in some countries). This study was done among the EU Member States between 1994 and 2001 and was subsequently replaced by EU Study of Income and Living Conditions. EU-SILC initially comprised only six Member States, with other countries joining in later years. ECHP did not cover any of the transition countries, but it is a great source of data for early years in benchmark countries. EU-SILC only covers transition countries from 2005 onwards and thus is less useful for the analysis of the wage compression in transition.

1.5 Living Standards Measurement Survey (LSMS)

Recognizing data shortage, The World Bank initiated standardized survey program with a number of developing countries, including the transition economies. It is a household budget survey with a number of modules in the questionnaire relating labor market status and wages. While LSMS is coordinated by The World Bank, it is usually implemented by statistical offices from the beneficiary countries. This implies that the wage module was not implemented in each country. Moreover, there can be some doubts concerning both the quality of the data (e.g. many missing values) and representativeness of the sample. LSMS sample sizes for comprise between app. 10,000 observations for smaller countries up to 30,000 individuals for larger countries. Data availability makes LSMS from three transition countries useful in our study: Albania, Armenia, Azerbaijan, Bulgaria, Bosnia and Herzegovina, Kazakhstan, Kyrgystan, Romania, Serbia and Tajikistan. Notably, for most of the countries there is no data on hours worked.

1.6 Russian Longitudinal Monitoring Survey (RLMS)

Prepared and conducted together by Carolina Population Center and Demoscope team, this is a unique project designed to track changes and effects of post-transition reforms on households and individuals in the Russian Federation. Currently data are available for years from 1994 to 2011. RLMS respondents report monthly net wage and hours worked.

1.7 Ukrainian Longitudinal Monitoring Survey (ULMS)

Ukrainian Monitoring Survey is an irregular study conducted by Insititue for the Study of Labor, IZA together with Kiev International Institute of Sociology. So far, three waves were conducted—in 2003, 2004 and 2007. ULMS was created to provide detailed information on households and labor force in Ukraine. It is nationally representative for working-age population. It includes both information on monthly wages and usual hours worked per week.

1.8 International Social Survey Programme (ISSP)

The International Social Survey Programme is one of the longest and most comprehensive dataset used in the study. In total program that started in 1984, includes now about 50 countries from all over the world. Unfortunately, national surveys are inconsistent both between years and within one country. Thus, we carefully selected countries and years for which question on monthly (or yearly) wages was asked. We excluded countries for which salaries were presented in categories, keeping only those with continous wage structure. For some countries, there are missing information on hours worked, so they are excluded from the analysis on the counterfactual wage distribution. Finally, excluding countries from outside of Europe, we were able to collect indicators for 19 countries (Table 2, 3; Fig. 3).

Table 2 Countries and periods covered with data sources

Table 3 Indicators of structural changes—descriptive statistics

Fig. 3

Source: Combined datasets described in the Table 2. Statistics for the working population aged 18–65

Characteristics of individuals across years.

Appendix 2: Robustness of Micro-derived Measures

See Tables 4, 5 and Fig. 4.

Table 4 Correlation between our and OECD measures of wage inequality

Table 5 Share of the variation of wage inequality measures attributed to time

Fig. 4

Source: counterfactual hourly wages of workers in two selected sources, countries and years—LFS France and in Slovakia from EU SES in 2010. Parametric counterfactual wages are obtained as fitted values from probit regression on sample of US population in ACS 1990 dataset and assigned to European workers based on gender, age group, education level and occupation. DFL counterfactual wages are weighted averages of hourly wages in US in 1990 in gender, age, education level and occupational groups

Comparison: individual hourly wages from parametric and DFL approach.

Appendix 3: Detailed Results and Sensitivity Analyses

See Figs. 5 and 6, Tables 6, 7, 8, 9 and 10.

Fig. 5

Source: monthly wages from data sources described in Table 2. Marginal effects of years obtained from regressions on wage compression measures and country, source, year and interaction of year and transition dummies as independent variables, robust variance estimator

Wage compression—predictive margins of year effects—monthly wage.

Fig. 6

Source: hourly wages, as described under Fig. 2. Marginal effects of years obtained from regressions on wage compression measures and country, source, year and interaction of year and transition dummies as independent variables, robust variance estimator

Wage compression—predictive margins of year effects—Gini index and MLD.

Table 6 Time trends in wage compression

Table 7 Time trends in wage compression

Table 8 Time trend and structural changes

Table 9 Wage compression and structural change

Table 10 Wage compression and the indicators of structural change—9th-to-1st