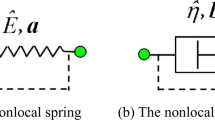
In this paper, a new viscoelastic constitutive model is proposed based on fractional-order differential theory, replacing the Newtonian dashpot of the classical Kelvin-Voigt model with the Abel dashpot. The analytic solutions for the fractional-order three-element model and classical three-element model are presented. The results estimated by the fractionalorder three-element model correlate better with experimental data than those of the classical three-element model. The parameters of the fractional-order three-element model were further optimized using the nonlinear least squares method. The proposed fractional-order three element model was able to accurately describe the viscoelastic dynamic mechanical properties of soil during vibratory compaction.
Similar content being viewed by others
References
A. Q. Shen, N. X. Zheng, and Y. Su, "Study of compacting mechanism and construction technology of filling road bed with bearing sand silt of low liquid limit," China J. Highway and Transport, 13(4), 12-15 (2000).
J. H. Qian, "The application of viscoelastic theory in soil mechanics," J. Natural Science of Higher Education, 2(1), 73-81 (1966).
D. S. Yin, J. J. Ren, C. L. He, and W. Chen, "The stress-strain relation of soft soil based on fractional calculus operators theory," Chin. J. Rock Mech. Eng., 28, 2973-2979 (2009).
H. H. Zhu, L. C. Liu, H. F. Pei, and B. Shi, "Settlement analysis of viscoelastic foundation under vertical line load using a fractional Kelvin-Voigt model," Geomech. Eng., 4(1), 67-78 (2012).
M. Liingaard, A. Augustesen, and P. V. Lade, "Characterization of models for time-dependent behavior of soils," Int. J. Geomech., 4(3), 157-177 (2004).
A. Gemant, "A method of analyzing experimental results obtained from elasto-viscous bodies," Physics, 7(8), 311-317 (2004).
F. Mainardi, "An historical perspective on fractional calculus in linear viscoelasticity," Fract. Calc. Appl. Anal., 15(4), 712-717 (2010).
I. Podlubny, Fractional Differential Equations, Academic press, San Diego (1999).
R. L. Bagley and P. J. Torvik, "A theoretical basis for the application of fractional calculus to viscoelasticity," Rheology, 27(3), 201-210 (1983).
R. C. Koeller, "Applications of fractional calculus to the theory of viscoelasticity," J. Appl. Mech., 51(2), 299-307 (1984).
S. W. J. Welch, R. A. L. Rorrer, and R. G. D. Jr, "Application of time-based fractional calculus methods to viscoelastic creep and stress relaxation of materials," Mech. Time-Depend Mat., 3(3), 279-303 (1999).
R. L. Bagleyand and P. J. Torvik, "On the fractional calculus model of viscoelastic behavior," Rheology, 30(1), 133-155 (1986).
W. Zhang and N. Shimizu, "Numerical algorithm for dynamic problems involving fractional operators," JSME Int. J., 41(3), 364-370 (1998).
Y. A. Rossikhin and M. V. Shitikova, "Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results," Appl. Mech. Rev., 63(1), 1-52 (2009).
N. Shimizu and W. Zhang, "Fractional calculus approach to dynamic problems of viscoelastic materials," JSME Int. J., 42(4), 825-837 (1999).
Y. A. Rossikhin and M. V. Shitikova, "A new method for solving dynamic problems of fractional derivative viscoelasticity," Int. J. Eng. Sci., 39(2), 149-176 (2001).
K. B. Oldham and J. Spanier, The Fractional Calculus, Academic Press, London (1974).
S. Millerand B. Ross, An Introduction to Fractional Calculus and Fractional Differential Equations, Wiley, New York (1993).
A. I. Zayed, Handbook of Function and Generalized Function Transformations, CRC Press, Florida (1996).
R. Gorenflo and M. Francesco, Essentials of Fractional Calculus, MaPhySto Center, Aarhus (2000).
S. G. Samko, A. A. Kilbas, and O. I. Marichev, Fractional Integrals and Derivatives and Some of Their Applications, Nauka i Technika, Minsk (1987).
J. H. Yin and F. Tong, "Constitutive modeling of time-dependent stress-strain behaviour of saturated soils exhibiting both creep and swelling," Can. Geotech. J., 48 (12), 1870-1885 (2011).
Z. Y. Yin, M. Karstunen, C. S. Chang, M. Koskinen, and M. Lojander, "Modeling time-dependent behavior of soft sensitive clay," J. Geotech. Geoenviron., 137 (11), 1103-1113 (2011).
V. O. Shestopal and P. C. Goss, "The estimation of column creep buckling durability from the initial stages of creep," Acta. Mech., 52(3-4), 269-275 (1984).
L. B. Eldred, W. P. Baker, and A. N. Palazzetto, "Kelvin-Voigt versus fractional derivative model as constitutive relations for viscoelastic materials," AIAA J., 33(3), 547-550 (2012).
A. Visintin, "Homogenization of the nonlinear Kelvin-Voigt model of viscoelasticity and of the Prager model of plasticity," Continuum Mech. Therm., 18(3-4), 223-252 (2006).
M. Bulicek, P. Kaplicky, and M. Steinhauer, "On existence of a classical solution to a generalized Kelvin-Voigt model," Pac. J. Math., 262(1), 11-33 (2013).
V. Venudharan, A. K. Chandrappa, K. P. Biligiri, and K. E. Kaloush, "Predictive models for storage modulus and loss modulus of asphalt mixtures," J. Mater. Civil Eng., 28(7), 04016038 (2016).
F. Cortes and M. Elejabarrieta, "Modelling viscoelastic materials whose storage modulus is constant with frequency," Int. J. Solids Struct., 43(25), 7721-7726 (2006).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Osnovaniya, Fundamenty i Mekhanika Gruntov, No. 6, p. 7, November-December, 2018.
Rights and permissions
About this article
Cite this article
Zhang, Q., Zhang, Q. & Ji, M. Dynamic Mechanical Properties of Soil Based on Fractional-Order Differential Theory. Soil Mech Found Eng 55, 366–373 (2019). https://doi.org/10.1007/s11204-019-09550-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11204-019-09550-5