1 Introduction

In the last decades, a new type of currency has been launched on the financial market and has gained importance.

Bitcoin is a special kind of asset called cryptocurrency. It was designed by Satoshi Nakamoto (allegedly a pseudonym of one person or a group of people) to work as a medium of exchange Nakamoto (2009). Since its introduction, it has been gaining more attention from the media, the finance industry, and academics. Contrary to ‘‘traditional’’ fiat currencies, bitcoin does not rely on any central authority but uses cryptography to control its creation and management. Some business already began accepting bitcoins in addition to national currencies (Williamson 2018). However, the legal status of bitcoin varies substantially from country to country.

There are several reasons for this interest: Firstly, Japan and South Korea have recognized Bitcoin as a legal method of payment (Bloomberg 2017a; Cointelegraph 2017). Second, some central banks are exploring the use of cryptocurrencies (Bloomberg 2017b). Third, the Enterprise Ethereum Alliance was created by a large number of companies and banks to make use of cryptocurrencies and the related technology called blockchain (Forbes 2017). Bitcoin (BTC) is based on decentralisation, which means that it is controlled and owned by its users. This decentralization is often criticized due to the lack of control over the whole system. Despite this criticism, Bitcoin increased in value from a couple of cents in the beginning (2009) to about 20,000 US dollars at the end of 2017. In China, cryptocurrency trade was banned in October 2017.

With Bitcoin’s increasing popularity, understanding how its prices are correlated with other financial assets is of interest to investors, regulators and policymakers.

As a peer-to-peer crypto-currency, Bitcoin holds the promise of being free from central banks’ and governments’ interventions. A decade after its inception following Satoshi Nakamoto’s (2008) vision, its price movements are far from being tamed nowadays. This study contributes to the existing literature on the empirical characteristics of virtual currency allowing for a dynamic transition between different economic regimes and considering various crashes and rallies over the business cycle, that is captured by jumps.

Stochastic volatility (SV) models are workhorses for the modeling and prediction of time-varying volatility on financial markets, and are essential tools in risk management, asset pricing and asset allocation. In financial mathematics and financial economics, stochastic volatility is typically modeled in a continuous-time setting which is advantageous for derivative pricing and portfolio optimization. Nevertheless, since data is typically only observable at discrete points in time, in empirical applications, discrete-time formulations of SV models are equally important. Volatility plays an important role in determining the overall risk of a portfolio and identifying hedging strategies that make the portfolio neutral concerning for to market moves. Moreover, volatility forecasting is also crucial in derivatives trading.

Recently, SV models allowing the mean level of volatility to ‘jump’ have been used in literature, see Chang et al. (2007) and Chib et al. (2002). The volatility of financial markets is a subject of constant analysis movements in the price of financial assets which directly affects the wealth of individuals, companies, charities, and other corporate bodies. Determining whether there are any patterns in the size and frequency of such movements, or their cause and effect, is critical in devising strategies for investments at the micro-level and monetary stability at the macro level. Shephard and Pitt (1997) used improved and efficient Markov Chain Monte-Carlo (MCMC) methods to estimate the volatility process ‘‘in block’’ rather than one point of time such as highlighted by Jacquier et al. (1994), for a simple SV model. Furthermore, Hsu and Chiao (2010) analyze the time patterns of individual analyst’s relative accuracy ranking in earnings forecasts using a Markov Chain model by treating two levels of stochastic persistence. Least squares and maximum likelihood techniques have long been used in parameter estimation problems. However, those techniques provide only point estimates with unknown or approximate uncertainty information. Bayesian inference coupled with the Gibbs Sampler is an approach to parameter estimation that exploits modern computing technology.

Kliber et al. (2019) apply the Stochastic Volatility Model with the Dynamic Conditional Correlation between main stock indices and the bitcoin price in the US dollar (Bitfinex exchange).

Baur and Lucey (2010) verified whether gold can be treated as a safe haven asset, estimating a regression model for the returns of gold, where the explanatory variables were the returns of bonds and stocks, as well as the bitcoin. It was also assumed that the error term from the regression model follows an asymmetric GARCH model.

Together with the development of the market of cryptocurrencies, many researchers like Smith (2018) and Kim (2018) started the debate over the possible role of the new asset from the investment perspective. One of the research hypotheses assumed that it can be treated as an alternative gold by some investors.

As noted by Pieters and Vivanco (2017), although bitcoin is indeed a homogeneous and identical virtual good across all online markets on which it is traded, its prices behave differently across these markets. Matkovskyy (2019) who compared the euro, U.S. dollar, and British pound sterling (GBP) with centralized and decentralized bitcoin cryptocurrency markets in terms of return volatility and interdependency. His results demonstrate that the markets differ for instance in terms of volatility which tends to be higher in the decentralized markets. Centralized markets have higher tail dependence regarding returns.

Our motivation for the research was to analyze the volatility of bitcoin using MCMC and detect if the bitcoin price converges and tends to zero like the other indices.

No study—to our knowledge has investigated in stochastic volatility using Metropolis Hasting, then assured comparison with other stock indices for the different international markets.

This paper is organized as follows, Sect. 2 presents the Bayesian approach and the MCMC algorithms. The SV model is introduced in Sect. 3, whereas empirical illustrations are given in Sect. 4.

2 The Bayesian approach and the MCMC algorithm

The Bayesian approach is a classical methodology where we assume that there is a set of unknown parameters. Alternatively, in the Bayesian approach, the parameters are considered as random variables with given prior distributions. We then use observations (the likelihood) to update these distributions and obtain the posterior distributions.

$$ P\left( {\theta /X} \right)\,\infty \,{\text{P}}({\text{X}}/\theta )*{\text{P}}(\theta ) $$

It would seem that to be subjective and to use the observations as much as possible, one should use non normative priors. However, this sometimes creates degeneracy issues and one should choose a different prior for this reason. Markov Chain Monte-Carlo (MCMC)includes the Gibbs Sampler as well as the Metropolis–Hastings (MH)algorithm.

2.1 The Metropolis Hasting

The Metropolis-Hasting is the baseline for MCMC schemes that simulate a Markov chain \( \theta^{\left( t \right)} \) with \( p(\theta /y \)) as the stationary distribution of a parameter h given a stock price index X. For example, we can define \( \theta_{1} , \theta_{2} \) and \( \theta_{3} \) such that \( \theta = \left( {\theta_{1} ,\theta_{2} ,\theta_{3} } \right) \) where each \( \theta_{i} \) can be scalar, vectors or matrices. Markov Chain Monte-Carlo algorithms are iterative and so at iteration t we will sample in turn from the three conditional distributions. Firstly, we update \( \theta_{1} \) by drawing a value \( \theta_{1}^{\left( t \right)} \) from \( p(\theta_{1} /Y,\theta_{2}^{{\left( {t - 1} \right)}} ,\theta_{3}^{{\left( {t - 1} \right)}} ) \). Secondly, we draw a value for \( \theta_{2}^{\left( t \right)} \) from \( p(\theta_{2} /Y, \), \( \theta_{1}^{{\left( {t - 1} \right)}} ,\theta_{3}^{{\left( {t - 1} \right)}} ) \) and finally, we draw \( \theta_{{\begin{array}{*{20}c} 3 \\ {} \\ \end{array} }}^{\left( t \right)} \) from \( p(\theta_{3} /Y,\theta_{1}^{{\left( {t - 1} \right)}} ,\theta_{2}^{\left( t \right)} ). \)

We start the algorithm off by selecting initial values, \( \theta_{i}^{\left( 0 \right)} \), for the three parameters. Then sampling from the three conditional distributions, in turn, will produce a set of Markov chains whose equilibrium distributions can be shown to be the joint posterior distributions that we require.

Following Hastings (1970), a generic step from a MH algorithm to update the parameter \( \theta_{i} \) at iteration t as follows:

  1. 1.

    Sample \( \theta_{i}^{*} \) from the proposal distribution \( p(\theta_{i} /,\theta_{i}^{{\left( {t - 1} \right)}} ). \)

  2. 2.

    Calculate \( f = p_{t} \left( {\theta_{i}^{{\left( {t - 1} \right)}} /\theta_{i}^{*} } \right)/p_{t} \left( {\theta_{i}^{*} /\theta_{i}^{{\left( {t - 1} \right)}} } \right) \) which is known as the hasting ratio and which equal 1 for symmetric proposals as used in pure Metropolis sampling.

  3. 3.

    Calculate \( s_{t} = fp\left( {\theta_{i}^{*} /y,\emptyset_{i} } \right)/p_{t} \left( {\theta_{i}^{{\left( {t - 1} \right)}} /y,\theta_{i} } \right) \) where \( \emptyset_{i} = \left\{ \theta \right\}/\left\{ {\theta_{i} } \right\} \) is the acceptance ratio and gives the probability of accepting the proposed value.

  4. 4.

    Let \( \theta_{i}^{\left( t \right)} = \theta_{i}^{*} \) with probability \( min\left( {1, s_{t} } \right) \) otherwise let \( \theta_{i}^{\left( t \right)} = \theta_{i}^{{\left( {t - 1} \right)}} \)

A popular and more efficient method is the acceptance-rejection (A-R) M-H sampling method which is available. Whenever the target densities are bounded by a density from which it is easy to sample.

2.2 The Gibbs sampler

The Gibbs sampler (Casella and George 1992; Gelfand and Smith 1990; Gilks and Wild 1992) is the special M-H algorithm whereby the proposal density for updating \( \theta_{j} \) equals the full conditional \( p(\theta_{j}^{*} /,\theta_{j} ). \) So that proposals are accepted with probability 1.

The Gibbs sampler involves parameter-by-parameter or block-by-block updating, which when completed from the transaction from \( \theta^{\left( t \right)} \) to \( \theta^{{\left( {t + 1} \right)}} \).

  1. 1.

    \( \theta_{1}^{{\left( {t + 1} \right)}} \sim f_{1} \left( {\theta_{1} /\theta_{2}^{t} ,\theta_{3}^{\left( t \right)} , \ldots \theta_{D}^{\left( t \right)} } \right). \)

  2. 2.

    \( \theta_{2}^{{\left( {t + 1} \right)}} \sim f_{2} \left( {\theta_{2} /\theta_{1}^{t + 1} ,\theta_{3}^{\left( t \right)} , \ldots \theta_{D}^{\left( t \right)} } \right). \)

  3. 3.

    \( \vdots \)

  4. 4.

    \( {\text{D}}. \theta_{D}^{{\left( {t + 1} \right)}} \sim f_{D} \left( {\theta_{D} /\theta_{1}^{t + 1} ,\theta_{3}^{{\left( {t + 1} \right)}} , \ldots \theta_{D - 1}^{{\left( {t + 1} \right)}} } \right). \)

Repeated sampling from M-H samplers such as the Gibbs samplers generates an autocorrelated sequence of numbers that, subject to regularity condition (ergodicity, etc.), eventually ‘forgets’ the starting values \( \theta^{0} = \left( {\theta_{1}^{\left( 0 \right)} ,\theta_{2}^{\left( 0 \right)} , \ldots ,\theta_{D}^{\left( 0 \right)} } \right) \) used to initialize the chain, and converges to a stationary sampling distribution \( p(\theta /y \)).

In practice, Gibbs and M-H algorithms are often combined, which results in a ‘‘hybrid’’ MCMC procedure.

3 The stochastic volatility model

3.1 Autoregressive SV model with studient’s distribution

In this paper, we will consider the p-th order ARSV-t model, ARSV(p)-t, as follows:

$$ \left\{ {\begin{array}{*{20}l} {y_{t} = \sigma \xi_{t} exp\left( {\upsilon_{t} /2} \right)} \hfill \\ {v_{t} = \phi_{1} v_{t - 1} + \cdots + \phi_{p} v_{t - p} + \eta_{t - 1} } \hfill \\ \end{array} } \right. $$
$$ \xi_{t} = \frac{{\varepsilon_{t} }}{{\sqrt {\kappa_{t} /(\nu } - 2)}}\quad {\text{with}}\quad \kappa_{t} \sim \chi^{2} \left( \nu \right) $$

where νt is independent of (εt, ηt), and vt is the log volatility which is assumed to follow a stationarity AR(p) process with a persistent parameter φ <1. By this specification, the conditional distribution, ξt, follows the standardized t-distribution with mean zero and variance one. Since κt is independent of (st, ηt), the correlation coefficient between ξt and ηt is also ρ.

If \( \phi \sim N\left( {0,100} \right) \), then:

$$ \emptyset_{1} = \frac{{\left( {\mathop \sum \nolimits_{t = 1}^{T} v_{t} v_{t - 1} } \right) - \emptyset_{2} \left( {\mathop \sum \nolimits_{t = 1}^{T} v_{t} v_{t - 2} } \right) + \overline{{\emptyset_{1} }} }}{{\left( {\mathop \sum \nolimits_{t = 1}^{T} v_{t - 1}^{2} } \right) - 1}} $$

And

$$ \emptyset_{2} = \frac{{\left( {\mathop \sum \nolimits_{t = 2}^{T} v_{t} v_{t - 2} } \right) - \emptyset_{1} \left( {\mathop \sum \nolimits_{t = 2}^{T} v_{t - 1} v_{t - 2} } \right) + \overline{{\emptyset_{2} }} }}{{\left( {\mathop \sum \nolimits_{t = 2}^{T} v_{t - 2}^{2} } \right) - 1}} $$

The conditional posterior distribution of the volatility is given by:

$$ \varvec{p}\left( {\varvec{V}/{\varvec{\Theta}}, {\mathbf{Y}}} \right)\infty \varvec{e}^{{\left( {\frac{1}{{2\varvec{*\sigma }^{2} }}\left( {\mathop \sum \nolimits_{{\varvec{t} = 1}}^{\varvec{T}} \varvec{Y}_{\varvec{t}}^{2} \varvec{e}^{{ - \varvec{V}_{\varvec{t}} }} } \right) - \frac{1}{2}\mathop \sum \nolimits_{{\varvec{t} = 1}}^{\varvec{T}} \left( {\varvec{V}_{\varvec{t}} - \emptyset_{1} \varvec{V}_{{\varvec{t} - 1}} - \emptyset_{2} \varvec{V}_{{\varvec{t} - 2}} } \right)^{2} - \frac{1}{2}\mathop \sum \nolimits_{{\varvec{t} = 1}}^{\varvec{T}} \left( {\varvec{V}_{{\varvec{t} + 1}} - \emptyset_{1} \varvec{V}_{\varvec{t}} - \emptyset_{2} \varvec{V}_{{\varvec{t} - 2}} } \right)^{2} } \right)}} $$

The representation of the SV-t model in terms of a scale mixture is particularly useful in a MCMC context since it allows sampling a non-log-concave sampling problems into a log-concave one. This permits sampling algorithms which guarantee convergence infinite time (see Frieze et al. 1994) allowing log returns to be student-t-distributed naturally changes the behavior of the stochastic volatility process, in the standard SV model, a large value of |yt| induce large value of the vt.

3.2 Basic SVOL model

Jacquier et al. (1994), hereafter JPR, introduced Markov Chain technique (MCMC) for the estimation of the basic SVOL model with normally distributed conditional errors.

$$ \left\{ {\begin{array}{*{20}l} {Y_{t} = \sqrt {V_{t} } \varepsilon_{t}^{s} } \hfill \\ {\log \left( {V_{t} } \right) = \alpha + \delta \log \left( {V_{t - 1} } \right) + \sigma_{v} \varepsilon_{t}^{v} } \hfill \\ \end{array} } \right. $$
$$ \left( {\varepsilon_{t}^{s} ,\varepsilon_{t}^{v} } \right)\sim N\left( {0,I_{2} } \right) $$

Let Θ be the vectors of parameters of the basic SVOL(α, δ, σv), and V = (Vt)T

The basic SVOL specifies zero correlation, the errors of the mean and variance equations.

Briefly, the Hammersley-Clifford theorem states that having a parameter-set Θ, a state v and an observation y, we can obtain the joint distribution \( p(\Theta , {\text{V}}/{\text{Y)}} \) from \( p(\Theta , {\text{V}}/{\text{Y)}} \) and \( p({\text{V}}/\Theta ,{\text{Y)}} \), under some mild regularity conditions. Therefore by applying the theorem iteratively, we can break a complicated multidimensional estimation problem into many sample one-dimensional problems.

Creating a Markov Chain Θ(i)via a Monte Carlo process, the Ergodic Averaging theorem states that the time-average of a parameter will converge towards its posteriors mean.

The formula of Bayes factorize the posterior distribution likelihood function with the prior hypotheses:

$$ P\left( {\Theta ,V/Y} \right)\infty P\left( {Y/V,\Theta } \right)P\left( {V/\Theta } \right)P\left(\Theta \right) $$

where α is the intercept, δ the volatility persistence and σv is the standard deviation of the shock to logVt. We use a Normal-Gamma prior, so, the parameter α, δ ~ N and σ2 ~ Itt, then:

$$ P(\alpha ,\delta /\sigma_{v} ,V,{\text{Y}})\sim \prod P(V_{t} /V_{t - 1} ,\alpha ,\delta ,\sigma_{v} )P(\alpha ,\delta )\infty N $$

And for \( \sigma_{v} , \) we obtain:

$$ P(\sigma^{2} /\alpha ,\delta ,{\text{V}},{\text{Y}})\infty P(V_{t} /V_{T - 1} ,\alpha ,\delta ,\sigma_{v} )P\left( {\sigma_{v}^{2} } \right)\infty IG $$

4 Empirical illustration

4.1 The data

Bitcoin (BTC) daily price data from January 2010 to October 2019 was retrieved from the Coindesk Price Index (2017). Like the majority of researchers, we used the Coindesk Price Index Dyhrberg (2016) and Bouri et al. (2018). It lists the average price of bitcoin against the US dollar from leading trading platforms from around the globe. Thus, the movements of the index are driven by investors from all over the world and we cannot indicate the country of origin.

Five indices including S&P 500 (GSPC), Nikkei (N225), Nasdaq, Down Jones, and Euro Index (Stoxx) are chosen to represent different regions whose currencies top the share of Bitcoin trade. Bitcoin trading against the Chinese Yuan accounted for most of Bitcoin’s trading volume until China started to clamp down on digital currency exchanges in early 2017, eventually banning the trading of Bitcoin in September of 2017. Japan’s Yen then took over as the largest trading volume with the Japanese regulators adopted digital currency-friendly rules. The US Dollar and Euro are also among the top five most active Bitcoin trading currencies. The return is defined as:

$$ y_{t} = 100*\left( {logS_{t} - logS_{t - 1} } \right). $$

We used the last 2350 observations for all indices.

Table 1 reports the mean, standard deviation, median, and the empirical skewness as well as kurtosis of the five series. Outlines the summary statistics for the daily, data for all assets. Bitcoin’s mean returns are 0.805% for daily data. As expected, Bitcoin returns exhibit much higher volatility than the stock indices.

Table 1 Summary statistics for daily returns
Full size table

Another interesting statistic is the skewness; Bitcoin is the one with negative skewness. This indicates that the tail is at the left side of the distribution, so the probability of lower values than the mean is higher than the normal distribution, which has a skewness of zero. With a positive skewness, this is the case for the other indices, the opposite is true. As before, Bitcoin has the highest volatility due to the highest kurtosis comparing to the other indices.

4.2 Estimations of SV models

The standard SV model is estimated by running the Gibbs and A-R M-H algorithm based on 20,000 MCMC iterations, where 5000 iterations are used as a burn-in period.

Tables 2 and 3 show the estimation results in the basic SVOL model and the SV-t model of the daily indexes. α and δ are prior independent. The prior in δ is essentially flat over [0,1]. We impose stationarity for log(Vt) by truncating the prior of δ. Other priors for δ are possible.

Table 2 Estimation results for the SVOL models
Full size table
Table 3 Estimation results for the SV-t models
Full size table

Geweke (1994a) proposes alternative priors to allow the formulation of odds ratios for non-stationarity. Wheras Kim et al. (1998) center an informative Beta Prior to around 0.9.

Table 2 shows the results for the daily indexes. The posterior of δ are higher for the daily series.

The highest mean is − 0.1173, 0.0765, − 0.1945, − 0.1774, 0.1601 and − 0.1501.

Well, as the basic SVOL, there is no apparent evidence of a unit of volatility. There are other factors that can deflect this rate such as the marcoeconomics variable (inflation, interest rate).

The Leverage effect is directly modeled in the model of JPR (1994, 2004). Also, the volatility at time t can be positively or negatively influenced by the volatility at time t-1. Similarly, the coefficient associated with the shocks is significant and positive for all the indices. Similarly, it is high in the majority of observations. We deduce that the nature of the shock can have a remarkable influence on volatility. This will generate excessive volatility which is well observed on the bitcoin series. Without neglecting the other indexes. Our results are similar to those of where psychological biases represent an explanatory factor. Guney et al. (2017), Edgars et al. (2018), Walid and Ahmed (2020), Kraaijeveld and De Smedt (2020).

Table 3 explores the Metropolis Hasting estimates of the basic autoregressive SV-t model.

The estimates of φ is between 0.2086 and 0.6711, while those of σ are between 0. 013 and 0. 075.

Against, the posterior of φ for the SV-t model is located higher. This result confirms the typical persistence reported in the GARCH literature. After the result, the first volatility factors have lower persistence while the values of φ2 indicate the high persistence of the second volatility factors.

The second factorφ2 plays an important role in the sense that it captures extreme values, which may produce the leverage effect, then it can be considered conceivable.

The estimates of ρ are positive for the same cases except for Down Jones and S&P when the estimates is respectively − 0.0226 and − 0.0389. Using Metropolis Hasting for each data set, the innovations in the mean and volatility are negatively correlated. Negative correlations between mean and variance errors can produce a “Leverage” effect in which negative (positive) shocks to the mean are associated with increases (decreases)in volatility (Mbanga et al. 2018; Andersen et al. 2003; Black 1976; Caraiani and Calin 2019; Hung et al. 2020).

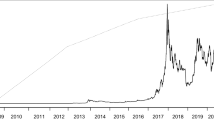
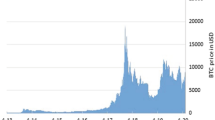
The return of different indexes is influenced by different crises observed in the international market (see Fig. 1) for example about bitcoin, the crash of April 2013 came after Bitcoin’s first significant brush with the mainstream. The currency had never crossed $30 before 2013 but a flood of media coverage helped drive it well above $200. Bitcoin spent most of the rest of 2013 around $120. Then prices jumped ten-fold in the fall: Bitcoin hit a high of $1150 in late November, and then the party ended abruptly, and prices tumbled below $500 by mid-December. It would take more than four years for Bitcoin to reach $1000 again.

Fig. 1
figure 1figure 1

Return for indexes

Full size image

Also, the price of Bitcoin had been making significant gains after 2013 when, in February, the price fell from $867 to $439 (a 49% drop). This triggered a doldrums period for Bitcoin that lasted until late 2016. The 6 February crash came after the operator of Mt. Gox-long the go-to trading place for longtime Bitcoin owners—announced the exchange had been hacked. On February 7, the exchange halted withdrawals and later revealed thieves had made off with 850,000 Bitcoins (which would be worth around $3.5 billion today). The incident, which created existential doubts about the security of Bitcoin and undercut liquidity in the currency, likely harmed the currency’s value for years.

Then in summer 2017: In early January, Bitcoin broke $1000 for the first time in years and started climbing like crazy. By June, the currency nudged $3000—but then lurched back all of a sudden, falling 36% to $1869 by mid-July.

The Great China Chill: After fears over the fork subsided, Bitcoin went on another crazy tear: It climbed close to $5000 at the start of September before plunging 37% by September 15, shaving off over $30 billion from Bitcoin’s total market cap in the process. Recovery is already underway, though, as prices climbed above $4000 three days later.

After 2017 was marked by tranquility in the financial markets, volatility finally rebounded in February and, most recently, in October and November 2018. Many financial analysts have indicated that these sudden increasing changes may be related to changes in expectations of the pace of monetary policy normalization US. Such increases would typically occur when inflation and employment figures are released.

More generally, the financial markets react to the publication of macroeconomic data, and in particular in the current context of international trade tensions. In all likelihood, therefore, do not exclude those specific events or the announcement inducing new bursts of volatility. Wu et al. (2019) prove the importance of the Economic Policy Uncertainty Index (EPU) in forecasting the volatility of Bitcoin prices.

More recently, stock market volatility was relatively high in 2015—when the fall of Chinese stock indices spread to the United States and Europe—and when Brexit was voted in mid-2016. Volatility then drastically decreased until 2018, when two corrections occurred on the US and European stock markets in February and October revived it.

Recently, researchers have discovered a significant influence on the cycle of business on the low-frequency component of volatility, while the abrupt increases in volatility partly due to reversals of market sentiment (Adrian and Rosenberg 2008; Engle and Rangel 2008; Engle et al. 2013; Corradi et al. 2013; Chiu et al. 2018; Rognone et al. 2020; Guégan and Renault 2020).

Developing in concert with measures of US volatility, the volatility of euro area stock markets began to decrease after the Brexit vote held in mid-2016. The Stoxx index at 1 month which measures the implied volatility of the Euro Stoxx 50 index—stood at 10% at the end of 2017, i.e. a level comparable to that before the crisis. This drop-in volatility was probably partly due to the good economic conditions of the moment and with a resolutely accommodating orientation of monetary policy (see also ECB 2017).

In February 2018, however, market volatility suddenly increased after the release of relative figures inflation and employment in the United States. These figures suggested that the Fed could normalize its policy faster than expected, which caused the stock market indices to fall. The Stoxx indices at 1 month jumped to 40 and 30% respectively. In the weeks that followed, these indices gradually declined to fall back to 12% in May. This episode, therefore, seems to be part of the high frequency component of volatility, that is, an increase in volatility (almost) unpredictable and without major consequences for the real economy.

In October 2018, a further correction occurred on the stock markets and volatility increased again.

The Stoxx one-month indices reached 21 and 25%. This event indicates that the markets remain particularly responsive to specific announcements in the context of a rate range recovery Fed director, declining net asset purchases by the ECB, trade and political tensions (Brexit, Italy).

We deduce also that the American market is volatile and this can be explained by the primordial role of investor sentiment in predicting the achievement of volatility based on the ranges of the S&P 500 index (Zhang and Mo 2019).

When the new information coming into the market, it can be disrupted and this affects the anticipation of shareholders for the evolution of the return.

The resulting plots of the smoothed volatilities are shown in Fig. 2. We take our analysis in the Bitcoin cryptocurrency, but the other is reported in Appendix 1 (Fig. 4).

Fig. 2
figure 2

Smoothed estimates of Vt Basic SVOL and SV-t model

Full size image

It is nicely illustrated that the technique of MCMC used for estimated the latent volatility reveals that the SV-t model is more performing than the SVOL. The convergence is very remarkable for the Nikkei, Down Jones, Stoxx, and the Bitcoin indices. This has proved that the algorithm used for estimated volatility is a good choice.

The basic SVOL model mis-specified can induce substantial parameter bias and error in inference about vt, Geweke (1994a, b) showed that the basic SVOL has the same problem with the largest outlier, summer 2017. The vt for the model SVOL reveals a big outlier on period crises.

The corresponding plots of innovation are shown in Fig. 3 for two model basic SVOL and SV-t model for Nikkei indices. Appendix B (Fig. 5) shows the QQ plot for the other indices respectively for the Nasdaq, S&P, the Down Jones, Nikkei and the Stoxx for the two models. The Quantile–Quantile plot can be used to determine whether two data sets come from populations with a common distribution. In this graphical technique, quantiles of the first data set against the quantiles of the second data set are plotted and a 45-degree reference line is used to interpret. If the two data sets come from a population with the same distribution the points should fall approximately along this reference line. The greater the departure from this reference line, the greater the evidence for the conclusion that the two data sets have come from populations with different distributions. This technique can provide an assessment of “goodness of fit” that is graphical and a more powerful approach than the common technique of comparing histograms of the samples.

Fig. 3
figure 3

QQ plot of normalized innovation based on the basic SVOL

Full size image

The advantages of Asymmetric basic SV are able to capture some aspects of the financial market and the main properties of their volatility behavior (Danielsson 1994; Eraker et al. 2003).

The following figure illustrates the Q–Q plot drawn to evaluate the fitted Scaled t-distribution graphically. In general, Q–Q plot demonstrates linear patterns which confirms that the two distributions considered in the graph are similar. Therefore, it can be said that the fitted Scaled t distributions with respective parameters exhibit a good fit for the return distribution for all indexes.

The algorithm used to estimate the volatility using the SV-t model ensures much higher normality for bitcoin than the SVOL.

Table 4 documents the performance of the algorithm and the consequence of using the wrong model on the estimates of volatility.

Table 4 MSE and AIC for two models
Full size table

The MCMC is more efficient for all parameters used in these two models. A certain threshold, all parameters are stable and converge to a certain level. Appendix C and D (Figs. 6 and 7) show that the α, δ, σ, φ converge and stabilize, this shows the power of MCMC.

The results for both simulated show that the algorithm of the SV-t model is fast and converges rapidly with acceptable levels of numerical efficiency. Then our sampling provides strong evidence of convergence of the chain.

5 Conclusion

Bitcoin is an innovative payment network and a new kind of money, then is a digital payment currency that utilizes crypto-currency and peer-to-peer technology to create and manage monetary transactions.

We have applied these MCMC methods to the study of various indexes and crypto-currency. The ARSV-t models were compared with SVOL models of JPR (1994) models using S&P, Down Jones, Nasdaq, Nikkei, and the STOXX. We wanted to study the behavior of this cryptocurrency, and it turned out that it behaves like the stock market indices of the different international markets facing different shocks (Efe Caglar (2019)).

The empirical results show that the SV-t model can describe extreme values to a certain extent and it is more appropriate to accommodate outlier. First, that the ARSV-t model provides a better fit than the MFSV model and second, the positive and negative shocks haven’t the same effect in volatility Manabu Asai (2008). Our result proves the efficiency of Markov Chain for our sample and the convergence and stability for all parameter to a certain level. Our results are consistent with the work of Dyhrberg (2016) and contradict those of Baur et al. (2018a, b) claim that bitcoin has unique risk-return characteristics, follows a different volatility process when compared with other assets. This view is endorsed by many researchers, e.g. Glaser et al. (2014) and Baek and Elbeck (2015a, b).

To our knowledge, no paper has processed bitcoin by conducting a comparative study using stochastic volatility models. Our results prove that this cryptocurrency does not behave differently from stock market indices although it is traded on a virtual market. Observing the market, several investors are wary of this cryptocurrency while justifying themselves by several considerations. Our results will help investors better diversify their portfolio by adding this cryptocurrency and this was clearly approved, especially after the “covid 19” crisis, where the volume of transactions has risen sharply in this type of market.

This paper has made certain contributions, but several extensions are still possible, and it can find the best results if you opt for extensions of SVOL like the model of Singleton (2001), knight et al. (2002) and others.