Abstract
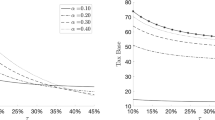
Standard discounted cash flow approaches suffer from a rudimental modeling of the possibility of a default, as the main characteristics such as the default probability and potential bankruptcy costs are commonly disregarded. This paper aims at providing a tractable extension of the well-known WACC approach for both default risk and bankruptcy costs. The corrected WACC discount rate reveals that default risk results in a systematically higher WACC because the tax component is scaled by the survivorship probability and an aditional component for bankruptcy costs must be added. This difference between the classical WACC discount rate and the simple modified WACC rate can be remarkable especially for firms from businesses with high bankruptcy costs and a relevant default probability.

Similar content being viewed by others
Notes
Noteworthy exceptions for DCF approaches dealing with bankruptcy are Cooper and Nyborg (2008), Molnar and Nyborg (2012). In these approaches the tax shield consequences for defaultable debt are quantified. However, the explicit default probability and bankruptcy costs are not considered and the resulting discount rate does not exhibit a tractable form.
Moosa and Li (2012) provide empirical determinants of firms’ capital structure choice.
The nominal interest rate c might contain a risk premium for default risk and bankruptcy costs. However, regardless of the size of c, the company cost of capital k V within the DCF approach ensure a consistent pricing of the firm value (see Fernandez (2012), topic 3) for the treatment of nominal interest rates.
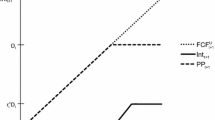
In the case in which only a default and a survivorship with full use of tax shields occurs, the expected level of tax shields is equal to the survivorship probability p and the expected level of bankruptcy costs equal to the default probability 1 − p.
References
Andrade G, Kaplan S (1998) How costly is financial (not economic) distress? Evidence from highly leveraged transactions. J Financ 53:1443–1493
Ang JS, Chua JH, McConnell JT (1982) The administrative costs bankruptcy: a note. J Financ 37:219–226
Báez-Díaz A, Alam P (2012) Tax conformity of earnings and the pricing of accruals. Forthcoming in Rev Quant Financ Account
Booth L (2002) Finding value where none exists: pitfalls in using adjusted present value. J Appl Corp Financ 15 (95–104)
Cooper IA, Nyborg KG (2006) Consistent methods of valuing companies by DCF: methods and assumptions. Working Paper
Cooper IA, Nyborg KG (2007) Valuing the debt tax shield. J Appl Corp Financ 19:50–59
Cooper IA, Nyborg KG (2008) Tax-adjusted discount rates with investor taxes and risky debt. Financ Manag 37:365-379
Couch R, Dothan M, Wu W (2012) Interest tax shields: a barrier options approach. Rev Quant Financ Account 39:123-146
Farber A, Gillet R, Szafarz A (2005) A general formula of the WACC. Working Paper
Fernandez P (2012) Ten badly explained topics in most corporate finance books. Working Paper
Fich EM, Slezak SL (2008) Can corporate governance save distressed firms from bankruptcy? An empirical analysis. Rev Quant Financ Account 30:225–251
Graham J (2001) Estimating the tax benefits of debt. J Appl Corp Financ 14:42–54
Inselbag I, Kaufold H (1997) Two DCF approaches for valuing companies under alternative financing strategies (and how to choose between them). J Appl Corp Financ 10:114–122
Kraus A, Litzenberger RH (1973) A state-preference model of optimal financial leverage. J Financ 28:911–922
Laughton D, Guerrero R, Lessard D (2008) Real asset valuation: a back-to-basics approach. J Appl Corp Financ 20:46–65
Leland H (1994) Corporate debt value, bond covenants, and optimal capital structure. J Financ 49:1213–1252
Miles JA, Ezzell JR (1980) The weighted average cost of capital, perfect capital markets, and project life: a clarification. J Financ Quant Anal 15:719–730
Modigliani F, Miller MH (1963) Corporate income taxes and the cost of capital: a correction. Am Econ Rev 53:433-443
Molnar P, Nyborg KG (2012) Tax-adjusted discount rates: a general formula under constant leverage ratios. Eur Financ Manag (Forthcoming)
Moosa I, Li L (2012) Firm-specific factors as determinants of capital structure: evidence from Indonesia. Rev Pac Basin Financ Mark Pol 15:1150007-1150001-1150007-1150017
Myers SC (1974) Interactions of corporate financing and investment decisions: implications for capital budgeting. J Financ 29:1–25
Oded J, Michel A (2007) Reconciling DCF valuation methodologies. J Appl Financ 17:21–40
Ruback RS (2002) Capital cash flows: a simple approach to valuing risky cash flows. Financ Manag 31:85–103
Standard & Poor’s (2009) 2008 Annual global corporate default study and rating transitions
Wang AT, Yang S-Y (2007) A simplified firm value-based risky discount bond pricing model. Rev Pac Basin Financ Mark Pol 10:445–468
Warner JB (1977) Bankruptcy costs: some evidence. J Financ 32:337–347
Author information
Authors and Affiliations
Corresponding author
Appendix: WACC formula for multi-state case
Appendix: WACC formula for multi-state case
To account for a very general case of tax shields, in which the firm does not default but only obtains a part of the full tax shield, we can extend the model framework as follows:
Let the tax shields at time t + 1:
where \(\phi_{\tau}\in\left[ 0;1\right] \) denotes the fraction of the full tax shield \(\tau\cdot D_{t}\cdot c\) that is in effect at time t + 1. In the case of positive earnings, ϕ τ is obviously one, and in the case of a default in which the tax deductions cannot be used, ϕ τ amounts to zero. In other cases, ϕ τ can take values between zero and one which can be interpreted as a firm that is currently able to satisfy its interest payments but does not have positive earnings in order to take full advantage of their feasible tax shields. Hence, \(\phi_{\tau}\cdot\tau\cdot D_{t}\cdot c\) is the present value of tax shields that is obtained from carrying forward the tax deductions \(\tau\cdot D_{t}\cdot c\) to future periods. Technically speaking, ϕ τ is a random variable from the perspective of time t and realizations are observed at time t + 1. We impose the assumption that the distribution of the realization of ϕ τ at time t + 1 is known at time t. Hence, we no longer have two states in which ϕ τ can only be zero or one but now we can incorporate arbitrarily many cases with arbitrary distributions for ϕ τ.
We can apply a similar notion for the bankruptcy costs. Let us denote the bankruptcy costs at time t + 1 as:
where ϕ α denotes the fraction of bankruptcy costs that is in effect at time t + 1. Apparently, without a default ϕ α is zero and in the case of a default it amounts to one. However, in the case of a reorganization, in which both outcomes a liquidation and a recovery are thinkable, ϕ α can be between zero and one. In line with the modelling of the discount factor ϕ τ for tax shields, we also assume that the statistical distribution for ϕ α is known one period in advance.
When modifying Eq. (6) with the notation introduced in this appendix, we now obtain for the expectation of total wealth from holding a firm alive at time t for one more period:
The second equation is a straightforward consequence of the linearity of the expectation operator \({\mathbb{E}_{t}\left( \cdot\right) . }\) Combining this representation with the representation for the WACC discount factor in Eq. (5), we obtain:
As a result, the WACC discount is the company cost of capital k V reduced by a tax shield component and increased by a bankruptcy component. The tax shield term equals the well-known term \(\tau\cdot\frac{D}{V}\cdot c\) multiplied by the expected level \({\mathbb{E}_{t}\left( \phi_{\tau}\right). }\) The same is true for the bankruptcy term.
Rights and permissions
About this article
Cite this article
Koziol, C. A simple correction of the WACC discount rate for default risk and bankruptcy costs. Rev Quant Finan Acc 42, 653–666 (2014). https://doi.org/10.1007/s11156-013-0356-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11156-013-0356-x