Abstract
We compare the performance of cartel penalties that are proportional to a cartel’s revenue and cartel penalties that are proportional to the difference between the cartel price and the competitive price: the overcharge. Prior literature has shown that when the probability of cartel detection does not depend on the cartel price, penalties that are based on a cartel’s overcharge generate greater total surplus and consumer surplus than do penalties that are based on a cartel’s revenue. In contrast, we find that when the probability of detection depends on the cartel price, penalties that are based on revenue can generate greater total surplus and consumer surplus.


Similar content being viewed by others
Notes
For example, Taro Pharmaceuticals U.S.A., Inc. and Sandoz, Inc. were fined $205.7 million and $195 million respectively for involvement in a price fixing conspiracy (U.S. vs. Taro Pharmaceuticals U.S.A, Inc. (E.D. Pa., No. 2:20-CR-00214-RBS 7/23/20) and U.S. vs. Sandoz Inc. (E.D. Pa., No. 2:20-CR-00111-RBS 3/02/20)). Starkist Co. admitted to conspiring with other major canned tuna suppliers to “fix, raise, and maintain the prices of packaged seafood products” and agreed to a fine of $100 million (U.S. vs. Starkist Co. (N.D. Ca., No. 3:18-CR-00513-EMC 11/14/18)).
International Competition Network Cartels Working Group, “Setting Fines for Cartels in ICN Jurisdictions”, Report to the 16th Annual Conference, Porto (2017).
A number of cartel cases suggest that the probability of cartel detection is endogenous and depends on the cartel price. In the stainless steel cartel case, an investigation began as a result of buyers reporting a suspiciously large increase in prices to the European Commission (Levenstein et al., 2004). Anomalous pricing also created suspicions of collusion in the Nasdaq case (Christie and Schultz, 1995). In the auto parts cartel, the cartel members specifically set prices in order to avoid detection by buyers (In re Automotive Parts Antitrust Litigation (E.D. Mich,. No. 12-md-02311, 03/08/17)).
We analyze and build on the model of Katsoulacos et al. (2015) for comparability and analytical tractability. However, as the primary forces that underly our main results are more general, our conclusions are expected to hold under other demand or cost assumptions.
We consider leniency programs, which allow firms to report the cartel in exchange for reduced penalties, in the online appendix (see https://www.douglascturner.com/endogenous-detection-online-appendix/). Our results are qualitatively unchanged.
We assume that penalties depend only on the price in the period of detection and do not depend on the length of time that a cartel has operated. See Akyapi and Turner (2021) for an exploration of cartel penalties that depend on duration.
We write the defection profit as a function of the cartel price p. If \(p\le p^{m}\), the defecting firm infinitesimally undercuts the cartel price and the defecting firm’s price is \(p-\epsilon \). If \(p>p^{m}\), the defecting firm charges a price of \(p^{m}\).
This reflects the fact that, once a cartel has dissolved, evidence of collusion is less likely to be uncovered. Additionally, as the market is now competitive, buyers or other observers are less likely to form or report suspicions of collusion. We explore the possibility of detection after cartel breakdown in the online appendix (https://www.douglascturner.com/endogenous-detection-online-appendix/).
When a cartel reforms after detection, we again consider the initial price to be c. This reflects the expectation of competitive market conditions after detection. A large deviation from marginal cost pricing, or a high value of \(\phi (c,p)\), indicates a cartel may have reformed. Alternatively, we could assume that the market operates competitively for one period after detection and then a cartel reforms. Results are robust to this alternative assumption.
If a cartel does not form for any discount factor, we set \(\delta _{i}=1\) as a convention.
Certain mechanisms of cartel detection—such as internal whistleblowers, random auditing, or the uncovering of evidence in a separate antitrust investigation—are likely unrelated to the cartel price. \(\alpha _{0}\) captures the probability of detection due to these mechanisms.
If \(\gamma _{R}<1\) or \(\gamma _{O}<1\), cartels could profitably collude by ignoring the possibility of raising suspicions of collusion and setting prices such that the cartel is detected with certainty in every period: a price greater than \(c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\). Immediate detection after one period of collusion is inconsistent with empirical evidence (Levenstein and Suslow, 2006). In addition, the examples in footnote 5 suggest that cartels do not ignore the possibility of raising suspicions of collusion.
The continued detection of illegal cartels suggests this is a reasonable assumption.
Recall that no cartel forms for any \(\delta \) when \(\delta _{R}=1\).
Theorem 2 can also be understood by analyzing the ratio of a cartel’s penalty to its per-period profit: \(\frac{x_{R}(p)}{\pi (p)}=\frac{\gamma _{R}D(p)p}{D(p)(p-c)}=\frac{\gamma _{R}p}{p-c}\). As \(\alpha _{1}\rightarrow \infty \) and \(p\rightarrow c\), this ratio approaches \(\infty \) which implies that the penalty from collusion becomes infinitely larger then per-period profit.
Recall that the price is c if a cartel does not form. Also, note that the cartel price must exceed marginal cost if a cartel forms because collusion must be profitable.
Recall that no cartel forms for any \(\delta \) when \(\delta _{R}=1\).
Per-period profit in period t is \(\pi (p_{t})\), and the expected penalty in period t is \(\phi (p_{t-1},p_{t})x_{R}(p_{t})\). As \(p_{t},p_{t-1}\rightarrow c\), \(\pi (p_{t})\rightarrow \pi (c)=0\) and \(\phi (p_{t-1},p_{t})x_{R}(p_{t})\rightarrow \alpha _{0}x_{R}(c)>0\).
See the online appendix (https://www.douglascturner.com/endogenous-detection-online-appendix/) for details.
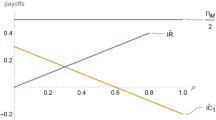
The monopoly price is 0.55. The overcharge-based cartel penalty when \(p=0.55\) is \(3.05(.55-0.1)D(0.1)\approx 1.24\). The revenue-based cartel penalty when \(p=0.55\) is \(5(0.55)D(0.55)\approx 1.24\).
Harrington (2004) makes a similar observation with regard to the limiting (or steady-state) cartel price (see Theorem 2 in Harrington (2004)). Recall that, as Katsoulacos et al. (2015) showed, the cartel price under revenue-based penalties is greater than the cartel price under overcharge-based penalties when the probability of detection is constant.
Revenue-based penalties have an additional advantage. Revenue-based penalties are less costly to calculate than alternative penalty types, because they require no information about a firm’s marginal cost or but-for price. Information on firm revenue is often readily available to investigators.
\(c\le p<\frac{1+c}{2}\) implies \(p(1-p)\ge H(c)\) because \(p(1-p)\ge c(1-c)\) if \(p<\frac{1}{2}\) and \(p(1-p)\ge \frac{1+c}{2}(1-\frac{1+c}{2})\) if \(p\ge \frac{1}{2}\).
The optimal price under aggregate overcharge-based penalties does not exceed the monopoly price. To see this, suppose that the optimal cartel price is \(p>p^{m}\). The cartel could increase profit and reduce the expected penalty by reducing the cartel price to \(p^{m}\). In addition, the payoff from defection is unchanged. Thus, \(p>p^{m}\) is not optimal.
If \(\pi (p)-\alpha _{0}x_{R}(p)\le 0\) for all \(p\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \), then \(W_{R}(p)=\frac{1}{1-\delta }\left[ \pi (p)-\phi x_{R}(p)\right] \le 0\) for all \(p\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \) (by \(\phi \ge \alpha _{0}\)) and collusion is unprofitable.
\(W_{R}(p;\alpha ''_{1},\delta )\le W_{R}(p;\alpha '{}_{1},\delta )\) if \(\alpha '_{1}<\alpha ''_{1}\) because
$$\begin{aligned} W_{R}(p;\alpha ''_{1},\delta )=\frac{(1-p)(p-c)-\phi (p;\alpha ''_{1})x_{R}(p)}{1-\delta }\le \frac{(1-p)(p-c)-\phi (p;\alpha '_{1})x_{R}(p)}{1-\delta }=W_{R}(p;\alpha '{}_{1},\delta ) \end{aligned}$$which follows from \(\phi (p;\alpha ''_{1})\ge \phi (p;\alpha '_{1})\), where \(\phi (p;\alpha _{1})=\min \{\alpha _{0}+\alpha _{1}(p-c)^{2},1\}\).
\(\alpha _{1}>{\bar{\alpha }}_{1}^{L}\ge \frac{9\left( 1-\alpha _{0}\right) }{(1-c)^{2}}>\frac{4\left( 1-\alpha _{0}\right) }{(1-c)^{2}}\) implies that \(p<c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\le c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\frac{4\left( 1-\alpha _{0}\right) }{(1-c)^{2}}}}\le c+(1-c)\frac{\sqrt{1-\alpha _{0}}}{2\sqrt{1-\alpha _{0}}}=\frac{1+c}{2}\).
Note that collusion is also profitable at price \(p_{R}+\epsilon \) under overcharge-based penalties because \(W_{O}(p_{R}+\epsilon )>W_{R}(p_{R})\ge \pi ^{D}(p_{R})>0\) where the last inequality follows from the fact that \(p_{R}>c\) by Lemma 1.
Suppose \(p_{i}>p_{i}^{NB}\) where \(i\in \left\{ O,R\right\} \). \(p_{i}\) is not optimal because \(W_{i}(p_{i}^{NB})>W_{i}(p_{i})\ge \pi ^{D}(p_{i})\ge \pi ^{D}(p_{i}^{NB})\) where the first inequality follows from the definition of \(p_{i}^{NB}\) and the strict concavity of \(W_{i}(p)\), the second inequality follows from the incentive compatibility of \(p_{i}\) and the last inequality follows from the observation that \(\pi ^{D}(p_{i})\) is nondecreasing. Thus, \(p_{i}^{NB}\) is incentive compatible and yields a greater collusive payoff.
Recall that L denotes the price-level specification and C denotes the price-change specification.
Specification L and specification C are equivalent when \(\alpha _{1}=0\).
Note that \(p_{1},p_{2},p_{3}\dots \) is sustainable when the price in the prior period was \(p_{t-1}\) because
$$\begin{aligned}&\pi (p_{1})-\phi (p_{t'-1},p_{1})x(p_{1})+\delta \left[ 1-\phi (p_{t'-1},p_{1})\right] V(p_{1})+\delta \phi (p_{t'-1},p_{1})V(c)\\ \ge&\pi (p_{1})-\phi (c,p_{1})x(p_{1})+\delta \left[ 1-\phi (c,p_{1})\right] V(p_{1})+\delta \phi (c,p_{1})V(c)\\ \ge&\pi ^{D}(p_{1}) \end{aligned}$$where the first inequality follows from \(\phi (p_{t'-1},p_{1})\le \phi (c,p_{1})\). The second inequality follows from the sustainability of \(p_{1}\) when the price in the prior period is c.
\(\pi (p)-\gamma _{R}p(1-p)=(1-p)(p(1-\gamma _{R})-c)=(1-p)(-p(\gamma _{R}-1)-c)=-(1-p)(p(\gamma _{R}-1)+c)\le 0\) and \(\pi (p)-\gamma _{O}Q_{N}(p-c)=(p-c)(1-p-\gamma _{O}Q_{N})\le (p-c)(1-c-\gamma _{O}Q_{N})=-(p-c)Q_{N}(\gamma _{O}-1)\le 0\).
\(V(p_{1})\ge V(c)\) because the probability of detection is a decreasing (or constant) function of the price in the previous period.
\(V(p_{t})\ge V(c)\) because the probability of detection is a decreasing (or constant) function of the price in the previous period.
If no cartel forms, then \(p_{t}=c\) for all \(t\ge 1\), and \(CS_{1}=\frac{CS(c)}{1-\delta }\).
Specifically, \(TS(p)=CS(p)+N\pi (p)\). If no cartel forms, then \(p_{t}=c\) for all \(t\ge 1\), and \(TS_{1}=\frac{TS(c)}{1-\delta }\).
References
Akyapi, B. & Turner, D. (2021). On the design of cartel penalties. In Working paper.
Bageri, V., & Katsoulacos, Y. (2014). A simple quantitative methodology for the setting of optimal fines by antitrust and regulatory authorities. European Competition Journal, 10(2), 253–278.
Bageri, V., Katsoulacos, Y., & Spagnolo, G. (2013). The distortive effects of antitrust fines based on revenue. The Economic Journal, 123(572), F545–F557.
Block, M. K., Nold, F. C., & Sidak, J. G. (1981). The deterrent effect of antitrust enforcement. Journal of Political Economy, 89(3), 429–445.
Bolotova, Y., Connor, J. M., & Miller, D. J. (2009). Factors influencing the magnitude of cartel overcharges: An empirical analysis of the us market. Journal of Competition Law and Economics, 5(2), 361–381.
Bos, I., Davies, S., Harrington, J. E., Jr., & Ormosi, P. L. (2018). Does enforcement deter cartels? A tale of two tails. International Journal of Industrial Organization, 59, 372–405.
Chen, Z., & Rey, P. (2013). On the design of leniency programs. The Journal of Law and Economics, 56(4), 917–957.
Christie, W. G., & Schultz, P. H. (1995). Policy watch: Did Nasdaq market makers implicitly collude? Journal of Economic Perspectives, 9(3), 199–208.
Dargaud, E., Mantovani, A., & Reggiani, C. (2016). Cartel punishment and the distortive effects of fines. Journal of Competition Law & Economics, 12(2), 375–399.
Garrod, L., & Olczak, M. (2018). Explicit vs tacit collusion: The effects of firm numbers and asymmetries. International Journal of Industrial Organization, 56, 1–25.
Harrington, J. E., Jr. (2004). Cartel pricing dynamics in the presence of an antitrust authority. RAND Journal of Economics, 35, 651–673.
Harrington, J. E., Jr. (2005). Optimal cartel pricing in the presence of an antitrust authority. International Economic Review, 46(1), 145–169.
Houba, H., Motchenkova, E., & Wen, Q. (2010). Antitrust enforcement with price-dependent fines and detection probabilities. Economics Bulletin, 30(3), 2017–2027.
Houba, H., Motchenkova, E., & Wen, Q. (2012). Competitive prices as optimal cartel prices. Economics Letters, 114(1), 39–42.
Houba, H., Motchenkova, E., & Wen, Q. (2015). The effects of leniency on cartel pricing. The BE Journal of Theoretical Economics, 15(2), 351–389.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2015). Penalizing cartels: The case for basing penalties on price overcharge. International Journal of Industrial Organization, 42, 70–80.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2018). Sophisticated revenue-based cartel penalties vs overcharge-based penalties. In School of Business and Economics Research Memorandum.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2019a). Penalizing cartels: A spectrum of regimes. Journal of Antitrust Enforcement, 7(3), 339–351.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2019b). Public and private antitrust enforcement for cartels: Should there be a common approach to sanctioning based on the overcharge rate? Revista de Economia Contemporanea, 23(2), 1–19.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2020a). Combining cartel penalties and private damage actions: The impact on cartel prices. International Journal of Industrial Organization, 73, 1–18.
Katsoulacos, Y., Motchenkova, E., & Ulph, D. (2020b). Penalising on the basis of the severity of the offence: A sophisticated revenue-based cartel penalty. Review of Industrial Organization, 57, 627–646.
Katsoulacos, Y., & Ulph, D. (2013). Antitrust penalties and the implications of empirical evidence on cartel overcharges. The Economic Journal, 123(572), F558–F581.
Levenstein, M. C., & Suslow, V. Y. (2006). What determines cartel success? Journal of Economic Literature, 44(1), 43–95.
Levenstein, M., Suslow, V. Y., & Oswald, L. J. (2004). Contemporary international cartels and developing countries: Economic effects and implications for competition policy. Antitrust Law Journal, 71, 801–852.
Motta, M., & Polo, M. (2003). Leniency programs and cartel prosecution. International Journal of Industrial Organization, 21(3), 347–379.
Acknowledgements
We thank David Sappington, Jeongwoo Lee, two anonymous refrees and the Editor Lawrence J. White for excellent comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: Proofs
1.1 Price-Level Specification
Let \(W_{R}(p)\) denote the present discounted value of profit less expected penalties under revenue-based penalties when the cartel price is p. Let \(W_{O}(p)\) denote the present discounted value of profit less expected penalties under overcharge-based penalties when the cartel price is p. \(p_{R}=\text {argmax}_{p\in [c,1]}W_{R}(p)\) subject to \(W_{R}(p)\ge \pi ^{D}(p)\) is the cartel price under revenue-based penalties, if a cartel forms. \(p_{O}=\text {argmax}_{p\in [c,1]}W_{O}(p)\) subject to \(W_{O}(p)\ge \pi ^{D}(p)\) is the cartel price under overcharge-based penalties, if a cartel forms.
Lemma 1 provides bounds on the cartel price, which necessarily hold if a cartel forms.
Lemma 1
\(p_{O}\in \left( c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \) and \(p_{R}\in \left( c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \) if a cartel forms.
Proof
If \(p_{R}=c\), the payoff from collusion is
which implies that collusion is not profitable.
If \(p_{R}\ge c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\), then the probability of detection is 1. Therefore, the payoff from collusion, when the cartel price is \(p_{R}\), is
which implies that collusion is not profitable (the first inequality follows from \(\gamma _{R}>1\)).
If \(p_{O}=c\), the payoff from collusion is
which implies that collusion is not profitable.
If \(p_{O}\ge c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\), then the probability of detection is 1. Therefore, the payoff from collusion, when the cartel price is \(p_{O}\), is
which implies that collusion is not profitable (the first inequality follows from \(\gamma _{O}>1\)). \(\square \)
Lemma 2
\(W_{R}(p)\) and \(W_{O}(p)\) are strictly concave on \(\left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \) if \(\alpha _{1}>\max \left\{ \left( \frac{5}{H(c)}\right) ^{2}(1-\alpha _{0}),\frac{4\left( 1-\alpha _{0}\right) }{(1-c)^{2}}\right\} \) where \(H(c)=\min \left\{ c(1-c),\left( \frac{1+c}{2}\right) \left( 1-\frac{1+c}{2}\right) \right\} \).
Proof
First, we consider revenue-based penalties. Note that \(W_{R}(p)=\frac{1}{1-\delta }\left( (1-p)(p-c)-\left( \alpha _{0}+\alpha _{1}(p-c)^{2}\right) \gamma _{R}p(1-p)\right) \) when \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \). The second derivative of \(W_{R}(p)\) when \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \) is
which is less than 0 if \(4(p-c)-2(p-c)^{2}-8p(p-c)+2p-2p^{2}\ge 0\). Note that \(p(1-p)\ge H(c)\) because \(c\le p\le c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}<\frac{1+c}{2}\) where the last inequality follows from \(\alpha _{1}>\frac{4\left( 1-\alpha _{0}\right) }{(1-c)^{2}}\).Footnote 33 Therefore,
Therefore, \(W_{R}(p)\) is strictly concave on \(\left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \).
Next, we show \(W_{O}(p)\) is strictly concave. Note that \(W_{O}(p)=\frac{1}{1-\delta }\left( (1-p)(p-c)-\left( \alpha _{0}+\alpha _{1}(p-c)^{2}\right) \gamma _{O}Q_{N}(p-c)\right) \) when \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \). The second derivative is
Therefore, \(W_{O}(p)\) is strictly concave when \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right] \). \(\square \)
Proof of Theorem 1
We show that a cartel forms when \(\delta >\delta _{O}\) and does not form when \(\delta \le \delta _{O}\). A cartel forms if collusion is sustainable and profitable. For collusion to be sustainable, collusion must be incentive-compatible: The constraint in Eq. (1) must hold. Note that the cartel price p satisfies both \(c<p<c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\), by Lemma 1, and \(p\le p^{m}\).Footnote 34 Collusion is sustainable at a price \(p=c+\epsilon \) where \(p\le p^{m}\) and \(p\in \left( c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \) if
If \(\delta >\delta _{O}=\frac{N-1}{N}+\frac{\alpha _{0}\gamma _{O}}{N}\), then there exists a sufficiently small \(\epsilon >0\) such that inequality (4) holds and collusion is sustainable. Collusion is also profitable at price \(p=c+\epsilon \) because
where the first inequality follows from \(c<p\le p^{m}\) and the second inequality follows from the sustainability of collusion at price \(p=c+\epsilon \). Therefore, collusion is profitable and sustainable if \(\delta >\delta _{O}\). If \(\delta \le \frac{N-1}{N}+\frac{\alpha _{0}\gamma _{O}}{N}\), collusion is unsustainable for all \(\epsilon \in \left( 0,\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \) (see inequality (4)) and unprofitable for \(\epsilon =0\) and \(\epsilon \ge \sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\) (see Lemma 1). Thus, a cartel does not form. \(\square \)
Proof of Theorem 2
First, we show \(\delta _{R}\rightarrow 1\) as \(\alpha _{1}\rightarrow \infty \). A cartel forms if collusion is sustainable and profitable. By Lemma 1, \(p\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \). We show collusion is unprofitable for all \(\delta <1\) if \(\alpha _{1}>\frac{(1-\alpha _{0})\left( 1-\alpha _{0}\gamma _{R}\right) ^{2}}{\left( \alpha _{0}\gamma _{R}c\right) ^{2}}\). Therefore, a cartel does not form and \(\delta _{R}=1\) if \(\alpha _{1}>\frac{(1-\alpha _{0})\left( 1-\alpha _{0}\gamma _{R}\right) ^{2}}{\left( \alpha _{0}\gamma _{R}c\right) ^{2}}\). For collusion to be profitable, \(\pi (p)-\alpha _{0}x_{R}(p)>0\) must hold for some price \(p\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \).Footnote 35 Note that
for all \(p\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \) where the last inequality follows from \(\alpha _{1}>\frac{(1-\alpha _{0})\left( 1-\alpha _{0}\gamma _{R}\right) ^{2}}{\left( \alpha _{0}\gamma _{R}c\right) ^{2}}\). Thus, collusion is unprofitable and a cartel does not form – \(\delta _{R}=1\)—if \(\alpha _{1}>\frac{(1-\alpha _{0})\left( 1-\alpha _{0}\gamma _{R}\right) ^{2}}{\left( \alpha _{0}\gamma _{R}c\right) ^{2}}\), which implies \(\delta _{R}\rightarrow 1\) as \(\alpha _{1}\rightarrow \infty \).
Next, we show \(\delta _{R}\rightarrow 1\) monotonically as \(\alpha _{1}\rightarrow \infty \). Let \(\delta _{R}(\alpha _{1})\) denote the critical discount factor when the sensitivity of the probability of detection to the overcharge is \(\alpha _{1}\). Suppose that \(\delta _{R}(\alpha '_{1})>\delta _{R}(\alpha ''_{1})\) for some \(\alpha '_{1}<\alpha ''_{1}\). Let \(\delta \) be such that \(\delta _{R}(\alpha ''_{1})<\delta <\delta _{R}(\alpha '_{1})\). A cartel forms when the discount factor is \(\delta \) if \(\alpha _{1}=\alpha ''_{1}\) and does not form if \(\alpha _{1}=\alpha '_{1}\). Let \(p''\) denote the cartel price when \(\alpha _{1}=\alpha ''_{1}\) and the discount factor is \(\delta \). Let \(W_{R}(p;\alpha _{1},\delta )\) denote the payoff from collusion when the cartel price is p, the sensitivity of the probability of detection to the overcharge is \(\alpha _{1}\) and the discount factor is \(\delta \). Note that \(\pi ^{D}(p'')\le W_{R}(p'';\alpha ''_{1},\delta )\) because collusion is sustainable when the cartel price is \(p''\). Also, note that \(0<W_{R}(p'';\alpha ''_{1},\delta )\) because collusion is profitable when the cartel price is \(p''\). However, \(\pi ^{D}(p'')\le W_{R}(p'';\alpha ''_{1},\delta )\le W_{R}(p'';\alpha '_{1},\delta )\) and \(0<W_{R}(p'';\alpha ''_{1},\delta )\le W_{R}(p'';\alpha '_{1},\delta )\) because \(\alpha '_{1}<\alpha ''_{1}\).Footnote 36 Thus, collusion is sustainable and profitable at a price of \(p''\) when \(\alpha _{1}=\alpha '_{1}\). This implies that a cartel forms when \(\delta <\delta _{R}(\alpha '_{1})\), which is a contradiction. Therefore, we conclude that \(\delta _{R}\rightarrow 1\) monotonically as \(\alpha _{1}\rightarrow \infty \). \(\square \)
Proof of Theorem 3
Let
where \(H(c)=\min \left\{ c(1-c),\left( \frac{1+c}{2}\right) \left( 1-\frac{1+c}{2}\right) \right\} \). Suppose that \(\alpha _{1}>{\bar{\alpha }}_{1}^{L}\).
The proof involves three steps: In step 1, we establish that the cartel price under overcharge-based penalties exceeds the cartel price under revenue-based penalties when \(\alpha _{1}>{\bar{\alpha }}_{1}^{L}\) and incentive compatibility constraints do not bind. This is proven by establishing that the derivative of the payoff from collusion under revenue-based penalties is negative at the unconstrained cartel price under overcharge-based penalties. In step 2, we establish that, when \(\alpha _{1}>{\bar{\alpha }}_{1}^{L}\), revenue-based penalties exceed overcharge-based cartel penalties. In step 3, we show, using the results from step 1 and step 2, that \(p_{R}<p_{O}\) generally.
Step 1: Let \(p_{i}^{NB}\) denote the cartel price when the incentive compatibility constraint does not bind under penalty type \(i\in \left\{ R,O\right\} \). First, we show \(p_{R}^{NB}<p_{O}^{NB}\). Note that \(p_{O}^{NB},p_{R}^{NB}\in \left( c,c+\frac{\sqrt{1-\alpha _{0}}}{\sqrt{\alpha _{1}}}\right) \) by Lemma 1. By the concavity of \(W_{O}(p)\) (Lemma 2), the first order condition which determines \(p_{O}^{NB}\) is
Solving for p yields
By the strict concavity of \(W_{R}(p)\) (Lemma 2), the first-order condition that determines \(p_{R}^{NB}\) is
Note that
where the first inequality follows from \(-\left( \alpha _{0}+\alpha _{1}(p-c)^{2}\right) \gamma _{R}(1-2p)<\gamma _{R}\) and the second inequality follows from \(p>c\). By the strict concavity of \(W_{R}(p)\), \(p_{R}^{NB}<p_{O}^{NB}\) if \(\frac{\partial W_{R}(p_{O}^{NB})}{\partial p}<0\).
where the last inequality follows from \(p_{O}^{NB}(1-p_{O}^{NB})\ge H(c)\), which follows from \(c<p_{O}^{NB}<\frac{1+c}{2}\).Footnote 37 Next, note that
which holds by (5). Therefore, \(\frac{\partial W_{R}(p_{O}^{NB})}{\partial p}<0\) and \(p_{R}^{NB}<p_{O}^{NB}\).
Step 2: Next, we show that revenue-based penalties are greater than overcharge-based penalties for all \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \). Note that
\(\gamma _{R}H(c)-\gamma _{O}Q_{N}\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}>0\) holds if
which holds by (5). Thus, \(x_{R}\left( p\right) >x_{O}\left( p\right) \) and \(W_{O}(p)>W_{R}(p)\) for all \(p\in \left[ c,c+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\right) \).
Step 3: Suppose \(p_{O}<p_{R}\). We show that \(p_{R}+\epsilon \), for sufficiently small \(\epsilon >0\), is incentive-compatible under aggregate overcharge-based penalties and achieves a greater payoff than \(p_{O}\). Therefore, \(p_{O}\) is not optimal. Note that
where the first inequality follows from \(W_{O}(p)>W_{R}(p)\) and the continuity of \(W_{O}(p)\). The second inequality follows from the incentive-compatibility of \(p_{R}\).Footnote 38 Thus, \(p_{R}+\epsilon \) is incentive compatible under overcharge-based penalties.
Next, note that \(p_{O}<p_{R}\le p_{R}^{NB}<p_{O}^{NB}\) which implies that \(p_{O}<p_{R}+\epsilon <p_{O}^{NB}\) for sufficiently small \(\epsilon >0\).Footnote 39 Therefore, \(W_{O}(p_{O})<W_{O}(p_{R}+\epsilon )\) by the strict concavity of \(W_{O}(p)\). We have shown \(p_{R}+\epsilon \) is incentive-compatible under overcharge-based penalties and results in a greater collusive payoff. Therefore, \(p_{O}\) is not the optimal cartel price, which is a contradiction. \(\square \)
Proof of Theorem 4
First, consider the case of \(\delta >\delta _{O}\). The proof follows from the observation that, by Theorems 1 and 2, there exists an \({\tilde{\alpha }}_{1}^{L}\) such that \(\delta _{R}>\delta >\delta _{O}\) if \(\alpha _{1}>{\tilde{\alpha }}_{1}^{L}\). Next, consider the case of \(\delta \le \delta _{O}\). When \(\delta \le \delta _{O}\), a cartel does not form under overcharge-based penalties (see the proof of Theorem 1). By Theorem 2, there exists an \({\tilde{\alpha }}_{1}^{L}\) such that \(\delta _{R}>\delta \) if \(\alpha _{1}>{\tilde{\alpha }}_{1}^{L}\). Thus, a cartel does not form under either penalty type when \(\alpha _{1}>{\tilde{\alpha }}_{1}^{L}\) which implies \(CS_{R}=CS_{O}\) and \(TS_{R}=TS_{O}\). \(\square \)
1.2 Changes Specification
Proof of Theorem 5
The proof involves two steps: First, we show a cartel forms when \(\delta >\delta _{O}\). Second, we show that a cartel does not form when \(\delta \le \delta _{O}\).
Suppose that \(\delta >\delta _{O}\). Let \(W_{O}^{j}(p)\) denote the payoff from collusion under specification \(j\in \left\{ L,C\right\} \) when the cartel price is p in all periods.Footnote 40 A cartel forms under specification L when \(\delta >\delta _{O}\) (see Theorem 1). Let \(p_{O}^{L}\) denote the cartel price under specification L. \(p_{O}^{L}>c\), and therefore \(\pi ^{D}(p_{O}^{L})>0\), by Lemma 1. In addition, \(W_{O}^{L}(p_{O}^{L})\ge \pi ^{D}(p_{O}^{L})\) because collusion must be sustainable for a cartel to form. Lastly, note that \(W_{O}^{C}(p)\ge W_{O}^{L}(p)\) for all p. Thus,
which implies that collusion is sustainable and profitable under specification C when \(\delta >\delta _{O}\) at a constant price of \(p_{O}^{L}\). Thus, a cartel forms under specification C when \(\delta >\delta _{O}\).
Next, suppose \(\delta \le \delta _{O}\) and a price path of \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) is sustainable and profitable under specification C. Let \(W_{O}^{j}\left( p_{t-1},\left\{ p_{t}\right\} _{t=1}^{\infty };\alpha _{1}\right) \) denote the present discounted value of collusion when: the prior period’s price is \(p_{t-1}\); the cartel price path is \(\left\{ p_{t}\right\} _{t=1}^{\infty }\); the sensitivity of the probability of detection to price is \(\alpha _{1}\) and the \(\phi \) specification is \(j\in \left\{ L,C\right\} \). First, note that \(W_{O}^{C}\left( p_{t-1},\left\{ p_{t}\right\} _{t=1}^{\infty };\alpha _{1}\right) \le W_{O}^{C}\left( p_{t-1},\left\{ p_{t}\right\} _{t=1}^{\infty };0\right) =W_{O}^{L}\left( p_{t-1},\left\{ p_{t}\right\} _{t=1}^{\infty };0\right) \) for all t.Footnote 41 As \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) is sustainable under specification C,
for all t. This implies that collusion is sustainable when \(\alpha _{1}=0\) and \(\delta \le \delta _{O}\) under specification L. Because the price path \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) is profitable under specification C,
which implies collusion is profitable when \(\alpha _{1}=0\) and \(\delta \le \delta _{O}\) under specification L. We have shown the price path \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) is profitable and sustainable when \(\alpha _{1}=0\) under specification L. Therefore, a cartel forms when \(\alpha _{1}=0\) and \(\delta \le \delta _{O}\) under specification L, which is a contradiction. \(\square \)
Lemma 3
\(p_{t}<p_{t-1}+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\) for all \(t\ge 1\) under both overcharge and revenue-based penalties.
Proof
Let \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) be an optimal price path where \(p_{t'}\ge p_{t'-1}+\sqrt{\frac{1-\alpha _{0}}{\alpha _{1}}}\) for some \(t'\) (and let \(t'\) denote the first such t). Note that \(\phi (p_{t'-1},p_{t'})=1\). The optimality of \(p_{t'},p_{t'+1},p_{t'+2}\dots \) implies that it yields a payoff that is greater than or equal to the payoff from the alternative price sequence of \(p_{1},p_{2},p_{3}\dots \) from \(t'\) onwards.Footnote 42 Thus,
Note that \(\pi (p_{t'})-x(p_{t'})\le 0\) because \(\gamma _{O}>1\) and \(\gamma _{R}>1\).Footnote 43 Thus, inequality (8) implies
or
Note that \(\pi (p_{1})-\phi (p_{t'-1},p_{1})x(p_{1})\ge \pi (p_{1})-\phi (c,p_{1})x(p_{1})\) because \(\phi (p_{t'-1},p_{1})\le \phi (c,p_{1})\). Also, note that \(\delta <1\). Thus, inequality (9) implies
Given that \(V(p_{1})\ge V(c)\),Footnote 44 inequality (10) holds only if \(\phi (p_{t'-1},p_{1})>\phi (c,p_{1})\) which is false. Therefore, \(p_{t'}\) is not optimal and the proof is complete. \(\square \)
Proof of Theorem 6
Note that, because the initial price is c, the cartel price in period t satisfies
where the inequalities follow from Lemma 3. Let \(T^{*}\) be such that \(T^{*}>2\) and \(\frac{\delta ^{T^{*}}}{1-\delta }<\frac{\alpha _{0}\gamma _{R}c}{2}D\left( \frac{1+c}{2}\right) \). Let
We show that collusion is unprofitable when \(\alpha _{1}>{\hat{\alpha }}_{1}^{C}\), and therefore a cartel does not form for all \(\delta <1\).
Suppose a cartel forms for some \(\alpha _{1}>{\hat{\alpha }}_{1}^{C}\). Let \(\left\{ p_{t}\right\} _{t=1}^{\infty }\) denote the cartel price path. First, observe that
where the first inequality follows from Lemma 3 and the second inequality follows from inequality (11).
Next, observe that
where the first, second and third inequalities follow from the observation that \(V(p_{t})\ge V(c)\) for all t.Footnote 45 The last inequality follows from \(\phi \ge \alpha _{0}\). Therefore,
We show \(A+C<0\) and \(B\le 0\)which implies \(V\left( c\right) <0\) and, therefore, a cartel does not form. First, note that
where the last inequality follows from \(p_{1}<\frac{1+c}{2}\) and the second to last inequality follows from Eq. (11):
Thus, we have shown \(A<-\frac{c\alpha _{0}\gamma _{R}}{2}D\left( \frac{1+c}{2}\right) \). \(B\le 0\) because
where the last inequality follows from Eq. (11):
Lastly, note that
where the first inequality follows from the observation that per-period profit is bounded above by 1. The second inequality follows from the definition of \(T^{*}\). Therefore, \(A+C<-\frac{c\alpha _{0}\gamma _{R}}{2}D\left( \frac{1+c}{2}\right) +\frac{c\alpha _{0}\gamma _{R}}{2}D\left( \frac{1+c}{2}\right) =0\). Thus, collusion is not profitable, and no cartel forms when \(\alpha _{1}>{\hat{\alpha }}_{1}^{C}\). This implies \(\delta _{R}\rightarrow 1\) as \(\alpha _{1}\rightarrow \infty \).
Next, we show \(\delta _{R}\rightarrow 1\) monotonically as \(\alpha _{1}\rightarrow \infty \). Let \(\delta _{R}(\alpha _{1})\) denote the critical discount factor when the sensitivity of the probability of detection to the change in price is \(\alpha _{1}\). Suppose \(\delta _{R}(\alpha '_{1})>\delta _{R}(\alpha ''_{1})\) for \(\alpha '_{1}<\alpha ''_{1}\). Let \(\delta \) be such that \(\delta _{R}(\alpha ''_{1})<\delta <\delta _{R}(\alpha '_{1})\). A cartel forms when the discount factor is \(\delta \) if \(\alpha _{1}=\alpha ''_{1}\) and does not form if \(\alpha _{1}=\alpha '_{1}\). Let \(\{p''_{t}\}_{t=1}^{\infty }\) denote the cartel price path when \(\alpha _{1}=\alpha ''_{1}\) and the discount factor is \(\delta \). Let \(W_{R}(p_{t-1},\{p_{t}\}_{t=1}^{\infty };\alpha _{1},\delta )\) denote the payoff from collusion when the cartel price path is \(\{p_{t}\}_{t=1}^{\infty }\), the prior period price is \(p_{t-1}\), the sensitivity of the probability of detection to the change in price is \(\alpha _{1}\) and the discount factor is \(\delta \).
Note that
for all t where the first inequality follows from the sustainability of collusion when \(\alpha _{1}=\alpha ''_{1}\). The second inequality follows from \(\alpha '_{1}<\alpha ''_{1}\). Also, note that
where the first inequality follows from the profitability of collusion when \(\alpha _{1}=\alpha ''_{1}\). The second inequality follows from \(\alpha '_{1}<\alpha ''_{1}\). Thus, collusion is sustainable and profitable with a price path of \(\{p''_{t}\}_{t=1}^{\infty }\) when \(\alpha _{1}=\alpha '_{1}\) and the discount factor is \(\delta \). Therefore, a cartel forms when \(\alpha _{1}=\alpha '_{1}\) which implies \(\delta >\delta _{R}(\alpha '_{1})\), a contradiction. We therefore conclude that \(\delta _{R}\rightarrow 1\) monotonically as \(\alpha _{1}\rightarrow \infty \). \(\square \)
Proof of Theorem 7
First, consider the case of \(\delta >\delta _{O}\). The proof follows from the observation that, by Theorems 5 and 6, there exists an \({\tilde{\alpha }}_{1}^{C}\) such that \(\delta _{R}>\delta >\delta _{O}\) if \(\alpha _{1}>{\tilde{\alpha }}_{1}^{C}\). Next, consider the case of \(\delta \le \delta _{O}\). When \(\delta \le \delta _{O}\), a cartel does not form under overcharge-based penalties (see the proof of Theorem 5). By Theorem 6, there exists an \({\tilde{\alpha }}_{1}^{C}\) such that \(\delta _{R}>\delta \) if \(\alpha _{1}>{\tilde{\alpha }}_{1}^{C}\). Thus, a cartel does not form under either penalty type when \(\alpha _{1}>{\tilde{\alpha }}_{1}^{C}\) which implies \(CS_{R}=CS_{O}\) and \(TS_{R}=TS_{O}\). \(\square \)
Appendix 2: Additional Derivations
In this section, we derive expressions for consumer surplus and total surplus.
Let the cartel’s price path be denoted \(\left\{ p_{t}\right\} _{t=1}^{\infty }\). Let \(CS_{t}\) denote the expected present discounted value of consumer surplus when the price in the prior period was \(p_{t-1}\). \(CS_{1}\) is the expected present discounted value of consumer surplus when the price in the prior period was c: the initial period or any period immediately after detection. Let \(CS(p_{t})\) denote per-period consumer surplus when the cartel price is \(p_{t}\) and let \(\phi _{t}=\phi (p_{t-1},p_{t})\).
If undetected in period t (which happens with probability \((1-\phi _{t})\)), the cartel continues into the next period (period \(t+1\)) with an initial price of \(p_{t}\). If detected (which happens with probability \(\phi _{t}\)), the cartel reforms with an initial price of c. Note that
Continuing this pattern yields
Solving for \(CS_{1}\) yields
where we let \(\prod _{\tau =1}^{0}\left[ 1-\phi _{\tau }\right] =1\) as a convention.Footnote 46
Computations analogous to those above show that the expected present discounted value of total surplus—the sum of consumer surplus and aggregate cartel profit—is
where \(\phi _{t}=\phi (p_{t-1},p_{t})\) and \(TS(p_{t})\) is total surplus when the cartel price is \(p_{t}\).Footnote 47
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Akyapi, B., Turner, D.C. Cartel Penalties Under Endogenous Detection. Rev Ind Organ 61, 341–371 (2022). https://doi.org/10.1007/s11151-022-09877-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-022-09877-8